上海市浦东新区建平香梅中学2023-2024学年数学八上期末达标检测模拟试题含答案

这是一份上海市浦东新区建平香梅中学2023-2024学年数学八上期末达标检测模拟试题含答案，共6页。试卷主要包含了考生必须保证答题卡的整洁，下面四个数中与最接近的数是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．下列等式成立的是（ ）
A．B．（a2）3=a6C．a2.a3 = a6D．
2．下列满足条件的三角形中，不是直角三角形的是（ ）
A．三内角之比为1：2：3B．三内角之比为3：4：5
C．三边之比为3：4：5D．三边之比为5：12：13
3．如图，已知，是边的中点，则等于（ ）
A．B．C．D．
4．已知，，是直线（为常数）上的三个点，则，，的大小关系是（ ）
A．B．C．D．
5．如图，在△中，，将△绕点顺时针旋转，得到△，连接，若，，则线段的长为（ ）
A．B．C．D．
6．下面四个数中与最接近的数是 （ ）
A．2B．3C．4D．5
7．已知点和在一次函数的图象上，则与的大小关系是（ ）
A．B．C．D．
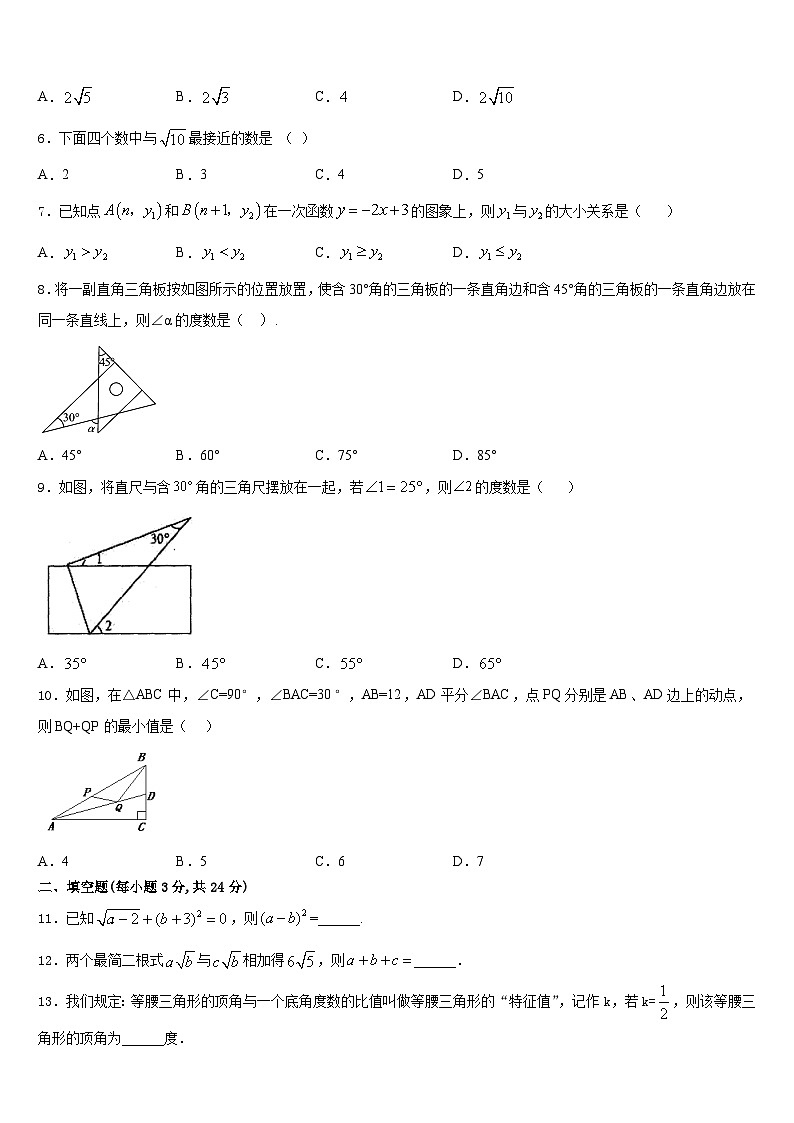
8．将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（ ）.
A．45°B．60°C．75°D．85°
9．如图，将直尺与含角的三角尺摆放在一起，若，则的度数是（ ）
A．B．C．D．
10．如图，在△ABC中，∠C=90°，∠BAC=30°，AB=12，AD平分∠BAC，点PQ分别是AB、AD边上的动点，则BQ+QP的最小值是（ ）
A．4B．5C．6D．7
二、填空题(每小题3分,共24分)
11．已知，则=______.
12．两个最简二根式与相加得，则______．
13．我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k=，则该等腰三角形的顶角为______度．
14．已知是一个完全平方式，则的值是_________________．
15．分解因式：m2+4m＝_____．
16．某校规定：学生的单科学期综合成绩是由平时、期中和期末三项成绩按3∶3∶4的比例计算所得．已知某学生本学期数学的平时、期中和期末成绩分别是90分、90分和95分，那么他本学期数学学期综合成绩是__________分
17．等腰三角形，，一腰上的中线把这个三角形的长分成12和15两部分，求这个三角形的底边______.
18．已知xy=3，那么的值为______ ．
三、解答题(共66分)
19．（10分）计算．
（1） （2）．
20．（6分）如图，AD是△ABC的中线，AB＝AC＝13，BC＝10，求AD长．
21．（6分）某工厂现在平均每天比原计划多生产25个零件，现在生产600个零件所需时间与原计划生产450个零件所需时间相同，原计划每天生产多少个零件？
22．（8分）如图，在正五边形ABCDE中，请仅用无刻度的直尺，分别按下列要求作图。
（1）在图1中，画出过点A的正五边形的对称轴；
（2）在图2中，画出一个以点C为顶点的720的角.
23．（8分）如图，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积.
24．（8分）某文具商店销售功能相同的A、B两种品牌的计算器，购买2个A品牌和3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需122元．
（1）求这两种品牌计算器的单价；
（2）学校开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器超出5个的部分按原价的七折销售，设购买x个A品牌的计算器需要y1元，购买x（x>5）个B品牌的计算器需要y2元，分别求出y1、y2关于x的函数关系式；
（3）当需要购买50个计算器时，买哪种品牌的计算器更合算？
25．（10分）化简分式，并在、、、、中选一个你喜欢的数作为的值，求代数式的值
26．（10分）（阅读理解）利用完全平方公式，可以将多项式变形为的形式，我们把这样的变形方法叫做多项式的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．
例如：
（问题解决）根据以上材料，解答下列问题：
（1）用多项式的配方法将多项式化成的形式；
（2）用多项式的配方法及平方差公式对多项式进行分解因式；
（3）求证：不论，取任何实数，多项式的值总为正数．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、C
4、B
5、A
6、B
7、A
8、C
9、C
10、C
二、填空题(每小题3分,共24分)
11、25
12、1
13、1
14、12或－12.
15、m(m+4)
16、1
17、7或1
18、±2
三、解答题(共66分)
19、（1）；（2）1
20、1
21、75.
22、见解析
23、1．
24、（1）A品牌计算器每个30元，B品牌计算器每个32元；（2）y1=24x，y2=22.4x+48（x＞5）；（3）B品牌合算．
25、-3
当=1时，原式=-2
26、（1），见解析；（2），见解析；（3）见解析