2024年中考数学圆训练专题-综合题型（六）（原卷+解析）

这是一份2024年中考数学圆训练专题-综合题型（六）（原卷+解析），文件包含2024年中考数学圆训练专题-综合题型六原卷docx、2024年中考数学圆训练专题-综合题型六解析docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。


（1）求证： ∠A=∠E ；
（2）若 BC=3 ， BE=5 ，求 CE 的长．
2．（2023·北京）如图， ⊙O 是 △ABC 的外接圆， AD 是 ⊙O 的直径， AD⊥BC 于点 E ．
（1）求证： ∠BAD=∠CAD ；
（2）连接 BO 并延长，交 AC 于点 F ，交 ⊙O 于点 G ，连接 GC ．若 ⊙O 的半径为5， OE=3 ，求 GC 和 OF 的长．
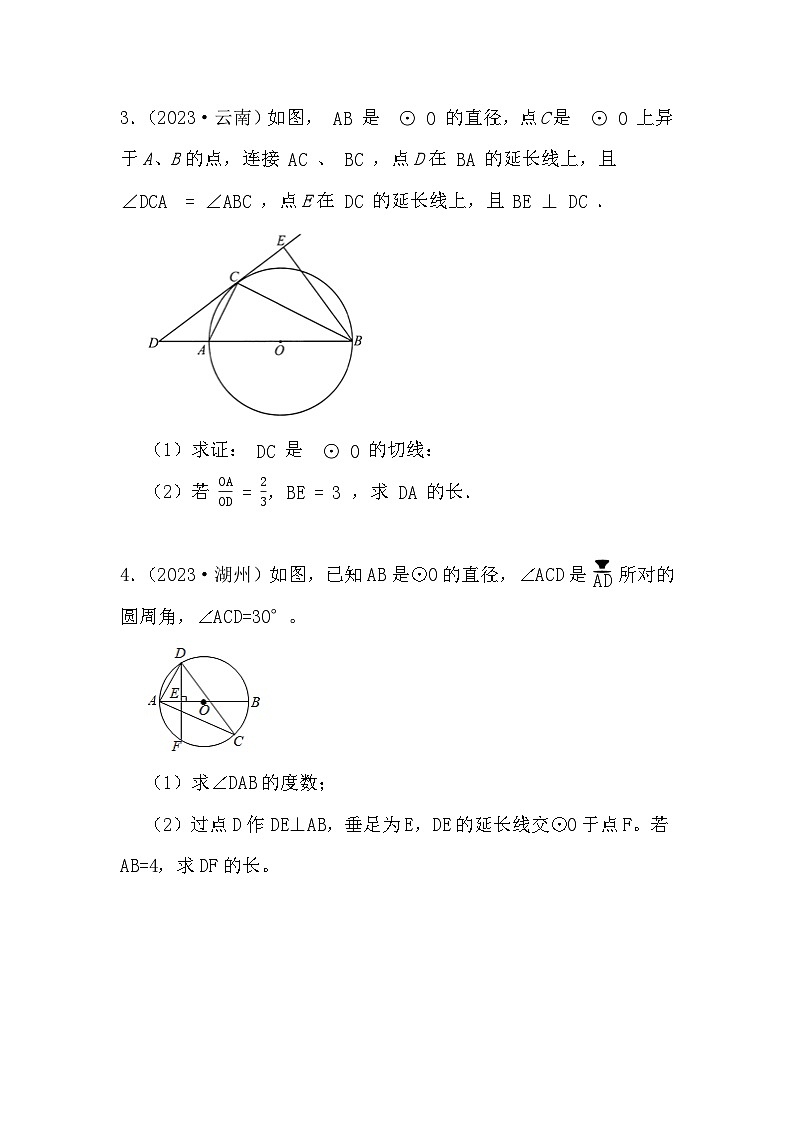
3．（2023·云南）如图， AB 是 ⊙O 的直径，点C是 ⊙O 上异于A、B的点，连接 AC 、 BC ，点D在 BA 的延长线上，且 ∠DCA=∠ABC ，点E在 DC 的延长线上，且 BE⊥DC ．
（1）求证： DC 是 ⊙O 的切线：
（2）若 OAOD=23，BE=3 ，求 DA 的长．
4．（2023·湖州）如图，已知AB是⊙O的直径，∠ACD是 AD 所对的圆周角，∠ACD=30°。
（1）求∠DAB的度数；
（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F。若AB=4，求DF的长。
5．（2023·丽水）如图，在△ABC中，AC＝BC，以BC为直径的半圆O交AB于点D，过点D作半圆O的切线，交AC于点E．
（1）求证：∠ACB＝2∠ADE；
（2）若DE＝3，AE＝ 3 ，求 CD 的长．
6．（2023.雅安）如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB，且CD＝AB，连接CB，与⊙O交于点F，在CD上取一点E，使EF＝EC.
（1）求证：EF是⊙O的切线；
（2）若D是OA的中点，AB＝4，求CF的长.
7．（2023.自贡）如图，AB是 ⊙O 的直径，AB=6，OC⊥AB，OC=5，BC与 ⊙O 交于点D，点E是 BD 的中点，EF∥BC，交OC的延长线于点F.
（1）求证：EF是 ⊙O 的切线；
（2）CG∥OD，交AB于点G，求CG的长.
8．（2023.遂宁）如图，四边形 ABCD 内接于 ⊙O，AC 是直径， AB=BC ，连接 BD ，过点 D 的直线与 CA 的延长线相交于点 E ，且 ∠EDA=∠ACD .
（1）求证：直线 DE 是 ⊙O 的切线；
（2）若 AD=6 ， CD=8 ，求 BD 的长.
9．（2023.广安）如图，已知 ΔABC ，以 AB 为直径的 ⊙O 交 AC 于点 D ，连接 BD ， ∠CBD 的平分线交 ⊙O 于点 E ，交 AC 于点 F ，且 AF=AB .
（1）判断 BC 所在直线与 ⊙O 的位置关系，并说明理由；
（2）若 tan∠FBC=13 ， DF=2 ，求 ⊙O 的半径.
10．（2023.德阳）如图， BC 是 ⊙O 的直径， AD 是 ⊙O 的弦， AD 交 BC 于点 E ，连接 AB,CD ，过点 E 作 EF⊥AB ，垂足为 F ， ∠AEF=∠D .
（1）求证： AD⊥BC ；
（2）点 G 在 BC 的延长线上，连接 AG,∠DAG=2∠D .
①求证： AG 与 ⊙O 相切；
②当 AFBF=25, CE=4 时，直接写出 CG 的长.
11．（2023.成都）如图，在 ⊙O 中，点 P 为 AB 的中点，弦 AD 、 PC 互相垂直，垂足为 M ， BC 分别与 AD 、 PD 相交于点 E 、 N ，连接 BD 、 MN .
（1）求证： N 为 BE 的中点.
（2）若 ⊙O 的半径为8， AB 的度数为 90° ，求线段 MN 的长.
12．（2023·大庆）如图，在 ΔABC 中， AB=AC ，以 AB 为直径的 ⊙O 交 BC 于点 D ，连接 AD ，过点 D 作 DM⊥AC ，垂足为 M ， AB 、 MD 的延长线交于点 N ．
（1）求证： MN 是 ⊙O 的切线；
（2）求证： DN2=BN⋅(BN+AC) ；
（3）若 BC=6 ， csC=35 ，求 DN 的长．