专题01 面积的存在性问题解题策略-2020年中考数学之存在性问题解题策略

这是一份专题01 面积的存在性问题解题策略-2020年中考数学之存在性问题解题策略，文件包含专题01面积的存在性问题解题策略原卷版doc、专题01面积的存在性问题解题策略解析版doc等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。

面积的存在性问题常见的题型和解题策略有两类：
第一类，先根据几何法确定存在性，再列方程求解，后检验方程的根．
第二类，先假设关系存在，再列方程，后根据方程的解验证假设是否正确．
例题解析
例❶ 如图1-1，矩形ABCD的顶点C在y轴右侧沿抛物线y＝x2－6x＋10滑动，在滑动过程中CD//x轴，CD＝1，AB在CD的下方．当点D在y轴上时，AB落在x轴上．当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时，求点C的坐标．
图1-1
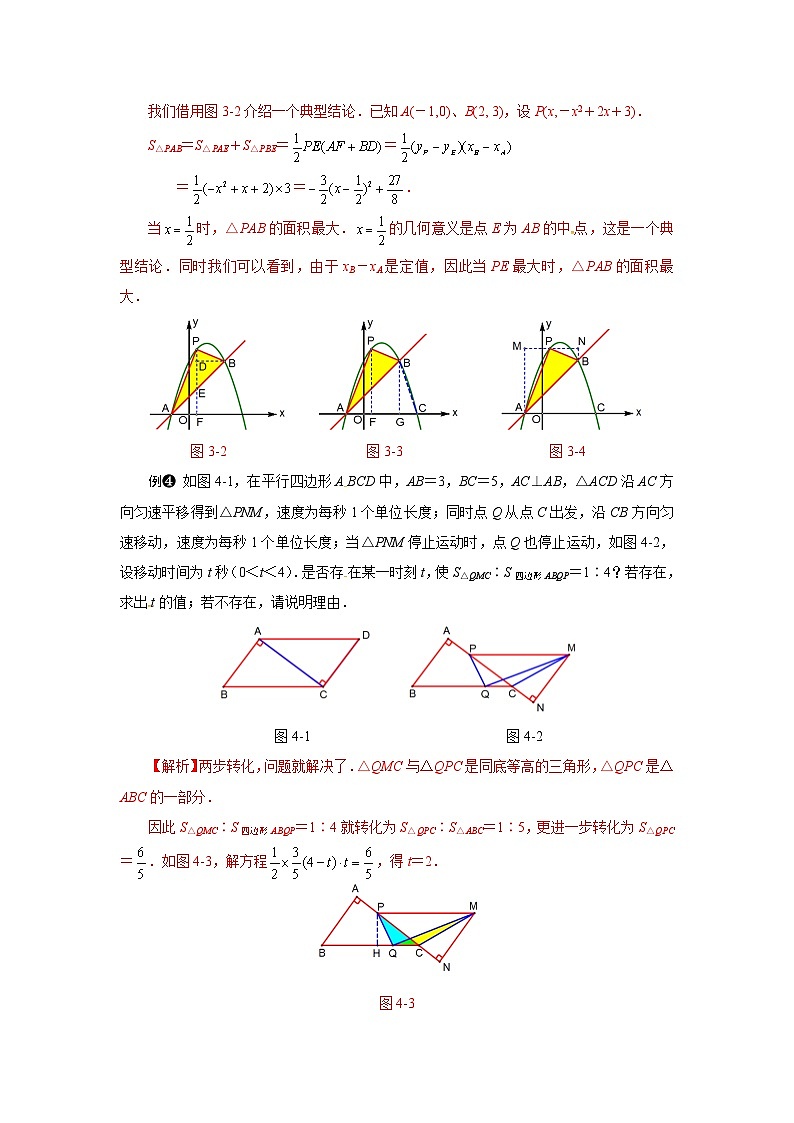
例❷ 如图2-1，二次函数y＝(x＋m)2＋k的图象与x轴交于A、B两点，顶点M的坐标为(1,－4)，AM与y轴相交于点C，在抛物线上是否还存在点P，使得S△PMB=S△BCM，如存在，求出点P的坐标．
图2-1
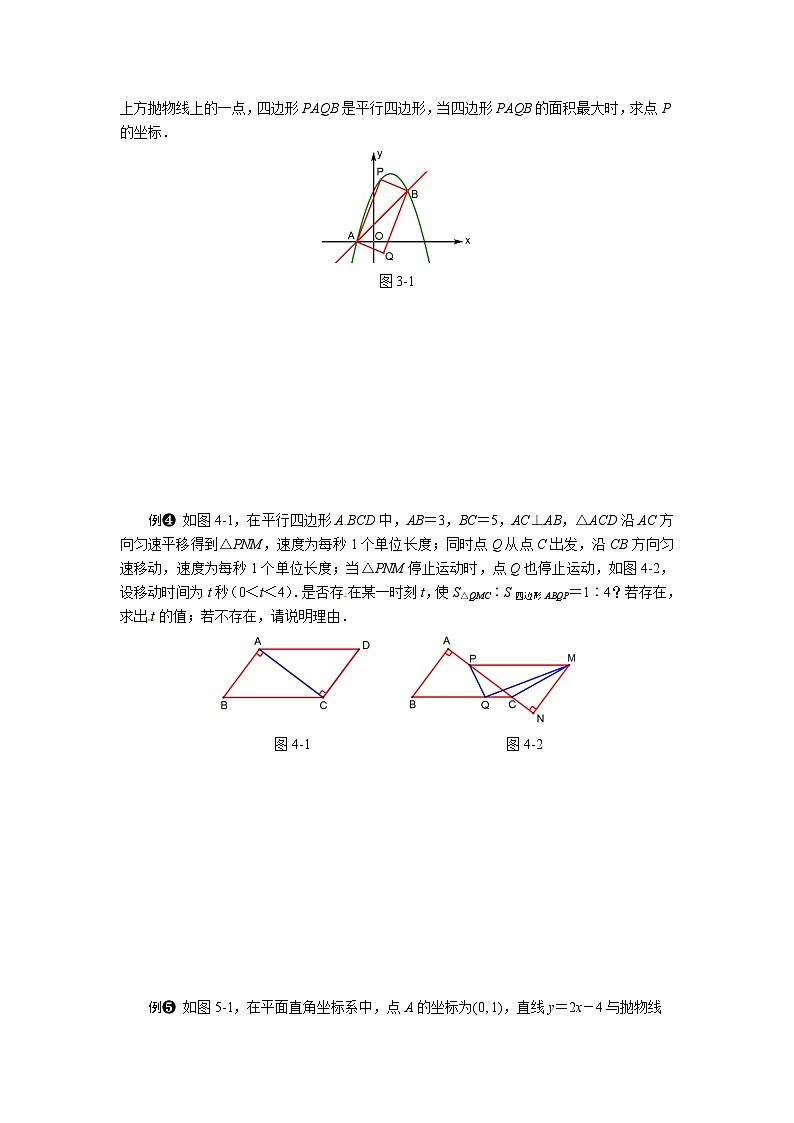
例❸ 如图3-1，直线y＝x＋1与抛物线y＝－x2＋2x＋3交于A、B两点，点P是直线AB上方抛物线上的一点，四边形PAQB是平行四边形，当四边形PAQB的面积最大时，求点P的坐标．
图3-1
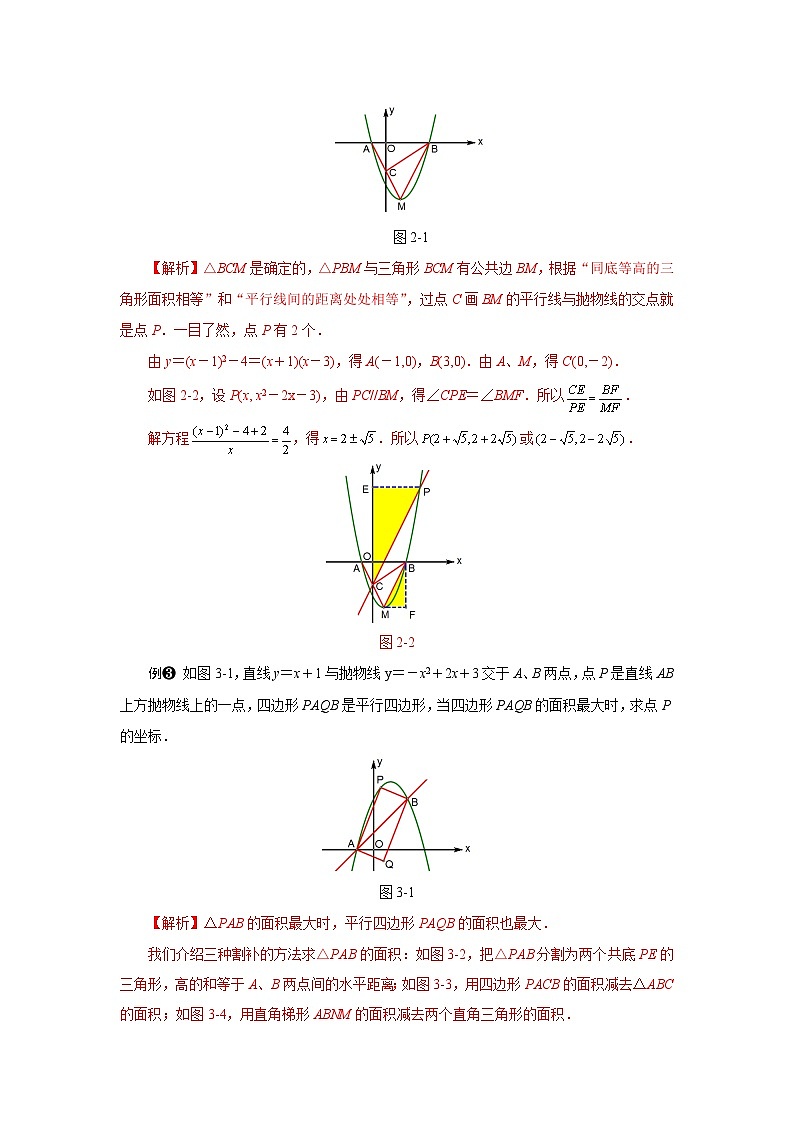
例❹ 如图4-1，在平行四边形ABCD中，AB＝3，BC＝5，AC⊥AB，△ACD沿AC方向匀速平移得到△PNM，速度为每秒1个单位长度；同时点Q从点C出发，沿CB方向匀速移动，速度为每秒1个单位长度；当△PNM停止运动时，点Q也停止运动，如图4-2，设移动时间为t秒（0＜t＜4）．是否存在某一时刻t，使S△QMC∶S四边形ABQP＝1∶4？若存在，求出t的值；若不存在，请说明理由．
图4-1 图4-2
例❺ 如图5-1，在平面直角坐标系中，点A的坐标为(0, 1)，直线y＝2x－4与抛物线相交于点B，与y轴交于点D．将△ABD沿直线BD折叠后，点A落在点C处（如图5-2），问在抛物线上是否存在点P，使得S△PCD＝3S△PAB？如果存在，请求出所有满足条件的点P的坐标；如果不存在，请说明理由．
图1 图2
例❻ 如图6-1，抛物线经过点E(6, n)，与x轴正半轴交于点A，若点P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形的面积记作S，则S取何值时，相应的点P有且只有3个？
图6-1
例❼ 如图7-1，点P是第二象限内抛物线上的一个动点，点D、E的坐标分别为(0, 6)、(－4, 0)．若将“使△PDE的面积为整数” 的点P记作“好点”，请写出所有“好点”的个数．
图7-1
例❽ 如图8-1，在平面直角坐标系中，已知点A的坐标为(a, 3)（其中a＞4），射线
OA与反比例函数的图象交于点P，点B、C分别在函数的图象上，且AB//x轴，AC//y轴．试说明的值是否随a的变化而变化？
图8-1
例❾ 如图9-1，已知扇形AOB的半径为2，圆心角∠AOB＝90°，点C是弧AB上的一个动点，CD⊥OA于D，CE⊥OB于E，求四边形ODCE的面积的最大值．
图9-1
例❿ 如图10-1，在△ABC中，∠C＝90°，AC＝6，BC＝8，设直线l与斜边AB交于点E，与直角边交于点F，设AE＝x，是否存在直线l同时平分△ABC的周长和面积？若存在直线l，求出x的值；若不存在直线l，请说明理由．
图10-1