2023-2024学年湖北省武汉市武昌区省水二中学八上数学期末学业水平测试模拟试题含答案

这是一份2023-2024学年湖北省武汉市武昌区省水二中学八上数学期末学业水平测试模拟试题含答案，共8页。试卷主要包含了答题时请按要求用笔，若分式等于零，则的值是，下列运算结果为的是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．在下列长度的三条线段中，不能组成三角形的是（ ）
A．2cm，3cm，4cmB．3cm，6cm，6cm
C．2cm，2cm，6cmD．5cm，6cm，7cm
2．下列语句是命题的是（ ）
（1）两点之间，线段最短；
（2）如果两个角的和是90度，那么这两个角互余.
（3）请画出两条互相平行的直线；
（4）过直线外一点作已知直线的垂线；
A．（1）（2）B．（3）（4）C．（2）（3）D．（1）（4）
3．点P（﹣1，2）关于x轴对称点的坐标为（ ）
A．（1，﹣2） B．（﹣1，2） C．（1，2） D．（﹣1，﹣2）
4．下列运算不正确的是（ ）
A．B．C．D．
5．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的大正方形．设直角三角形较长的直角边为，较短的直角边为，且，则大正方形面积与小正方形面积之比为（ ）
A．25：9B．25：1C．4：3D．16：9
6．若分式等于零，则的值是（ ）
A．B．C．D．
7．如图，在四边形中，，在上分别找到点M，N，当的周长最小时，的度数为（ ）
A．118°B．121°C．120°D．90°
8．.已知两条线段长分别为3,4,那么能与它们组成直角三角形的第三条线段长是( )
A．5B．
C．5或D．不能确定
9．下列长度的三根木棒能组成三角形的是（ ）
A．2 ，3 ，4B．2 ，2 ，4C．2 ，3 ，6D．1 ，2 ，4
10．下列运算结果为的是
A．B．C．D．
二、填空题(每小题3分,共24分)
11．在函数中，那么_______________________.
12．如图，一张矩形纸片沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形），则∠OCD等于_________．
13．若分式方程﹣＝2有增根，则a＝_____．
14．要使分式有意义，则x应满足条件____．
15．命题：“三边分别相等的两个三角形全等”的逆命题________
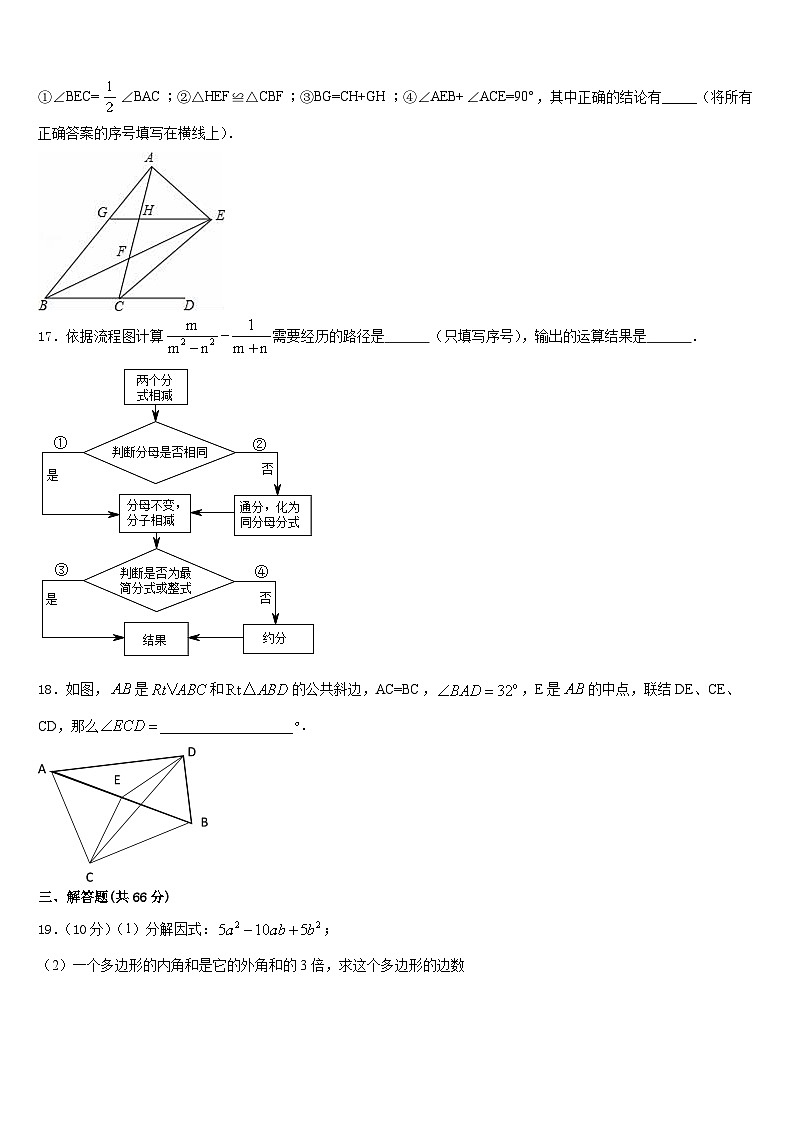
16．如图，△ABC的内角∠ABC和外角∠ACD的平分线相交于点E，BE交AC于点F，过点E作EG∥BD交AB于点G，交AC于点H，连接AE，有以下结论：
①∠BEC=∠BAC；②△HEF≌△CBF；③BG=CH+GH；④∠AEB+∠ACE=90°，其中正确的结论有_____（将所有正确答案的序号填写在横线上）．
17．依据流程图计算需要经历的路径是 （只填写序号），输出的运算结果是 ．
18．如图，是和的公共斜边，AC=BC，，E是的中点，联结DE、CE、CD，那么___________________．
三、解答题(共66分)
19．（10分）（1）分解因式：；
（2）一个多边形的内角和是它的外角和的3倍，求这个多边形的边数
20．（6分）已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
（发现）
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD= °，△CBD是 三角形；
（探索）
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
（应用）
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有 ．（只填序号）
①2个 ②3个 ③4个 ④4个以上
21．（6分）如图，已知四边形各顶点的坐标分别为．
（1）请你在坐标系中画出四边形，并画出其关于轴对称的四边形；
（2）尺规作图：求作一点，使得，且为等腰三角形．
（要求：仅找一个点即可，保留作图痕迹，不写作法）
22．（8分）如图，AC平分钝角∠BAE交过B点的直线于点C，BD平分∠ABC交AC于点D，且∠BAD+∠ABD＝90°．
（1）求证：AE∥BC；
（2）点F是射线BC上一动点（点F不与点B，C重合），连接AF，与射线BD相交于点P．
（ⅰ）如图1，若∠ABC＝45°，AF⊥AB，试探究线段BF与CF之间满足的数量关系；
（ⅱ）如图2，若AB＝10，S△ABC＝30，∠CAF＝∠ABD，求线段BP的长．
23．（8分）已知，在平面直角坐标系中，、，m、n满足．C为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO＝PD，DE⊥AB于E．
（1）如图1，当点P在线段AB上运动时，点D恰在线段OA上，则PE与AB的数量关系为 ．
（2）如图2，当点D在点A右侧时，（1）中结论是否成立？若成立，写出证明过程；若不成立，说明理由．
（3）设AB＝5,若∠OPD＝45°，直接写出点D的坐标．
24．（8分）某商场计划购进、两种新型节能台灯共盏，这两种台灯的进价、售价如表所示：
（）若商场预计进货款为元，则这两种台灯各购进多少盏？
（）若商场规定型台灯的进货数量不超过型台灯数量的倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
25．（10分）某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．
根据图示填写下表：
结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；
计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．
26．（10分）计算：（2﹣1）2﹣（）÷．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、D
4、D
5、B
6、C
7、A
8、C
9、A
10、D
二、填空题(每小题3分,共24分)
11、
12、126°
13、
14、x≠1．
15、如果两个三角形全等，那么对应的三边相等
16、①③④.
17、②③，．
18、1
三、解答题(共66分)
19、（1）；（2）八边形
20、（1）60，等边；（2）等边三角形，证明见解析（3）④.
21、见解析
22、（1）见解析；（2）（ⅰ）BF＝（2+）CF；理由见解析；（ⅱ）BP＝．
23、（1）AB＝2PE；（2）成立，理由见解析；（3）点D．
24、（1）购进型台灯盏，型台灯25盏；
（2）当商场购进型台灯盏时，商场获利最大，此时获利为元．
25、；85；1．（2）A校成绩好些． 校的方差，B校的方差．A校代表队选手成绩较为稳定．
26、9-5
平均数分
中位数分
众数分
A校
______
85
______
B校
85
______
100