+安徽省合肥市庐阳区2023-2024学年+九年级上学期数学期末模拟卷一

这是一份+安徽省合肥市庐阳区2023-2024学年+九年级上学期数学期末模拟卷一，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

姓名： 学号： 考号： 分数： 。
考生须知：
本试卷分试题卷和答题卷两部分，满分150分，考试时间120分钟。
答题前，必须在答题卡上填写校名，班级，姓名，座位号。
不允许使用计算器进行计算，凡题目中没有要求取近似值的，结果应保留根号或π
一、选择题（每小题4分，有10小题，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．若 a:b=3:4 ，且 a+b=14 ，则 2a-b 的值是（ ）
A．4B．2C．20D．14
2．若 A(2,4) 与 B(-2,a) 都是反比例函数 y=kx(k≠0) 图象上的点，则a的值是（ ）
A．4B．-4C．2D．-2
3．如图下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
4．用圆心角为120°，半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒（如图所示），则这个纸冒的高是（ ）
A．3 cmB．2 2 cmC．3 2 cmD．4 2 cm
5．如图，在△ABC中，点D，E分别在边AC，BC上，则不一定能判断△ABC∽△EDC的是（ ）
A．∠CDE＝∠BB．∠DEC＝∠AC．CDEC=CBACD．CDBC=DEBA
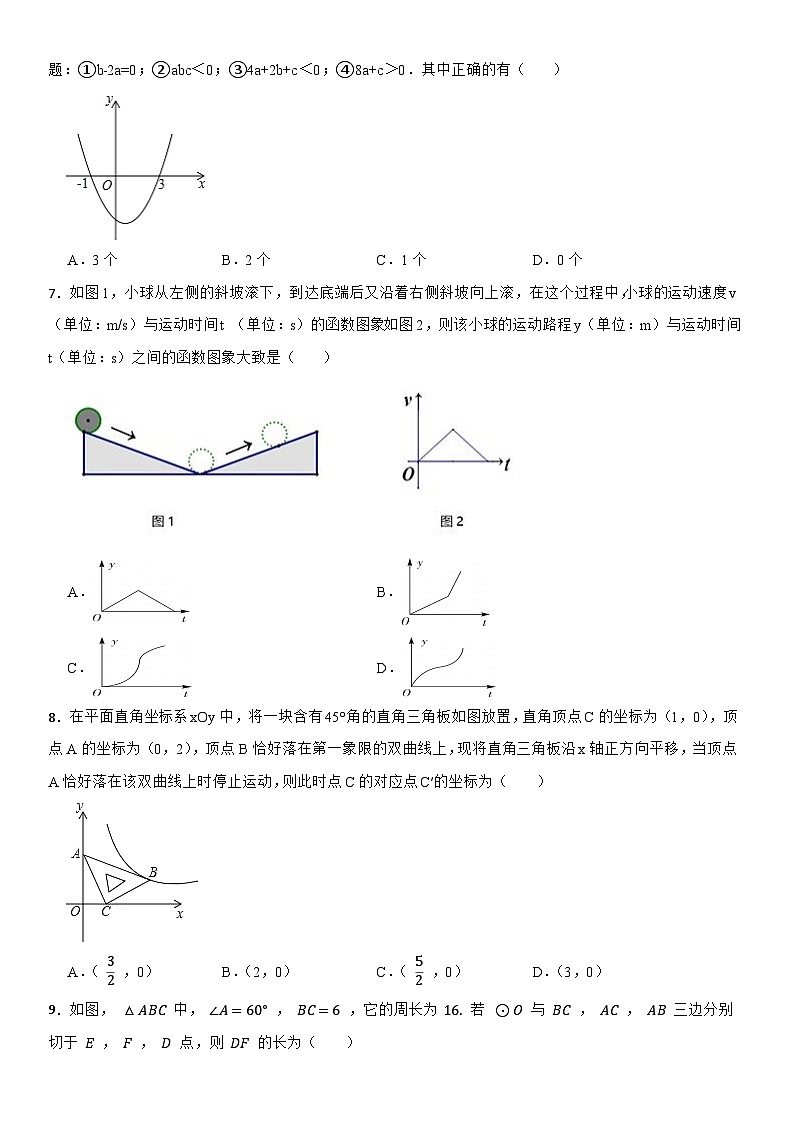
6．已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣2a=0；②abc＜0；③4a+2b+c＜0；④8a+c＞0．其中正确的有（ ）
A．3个B．2个C．1个D．0个
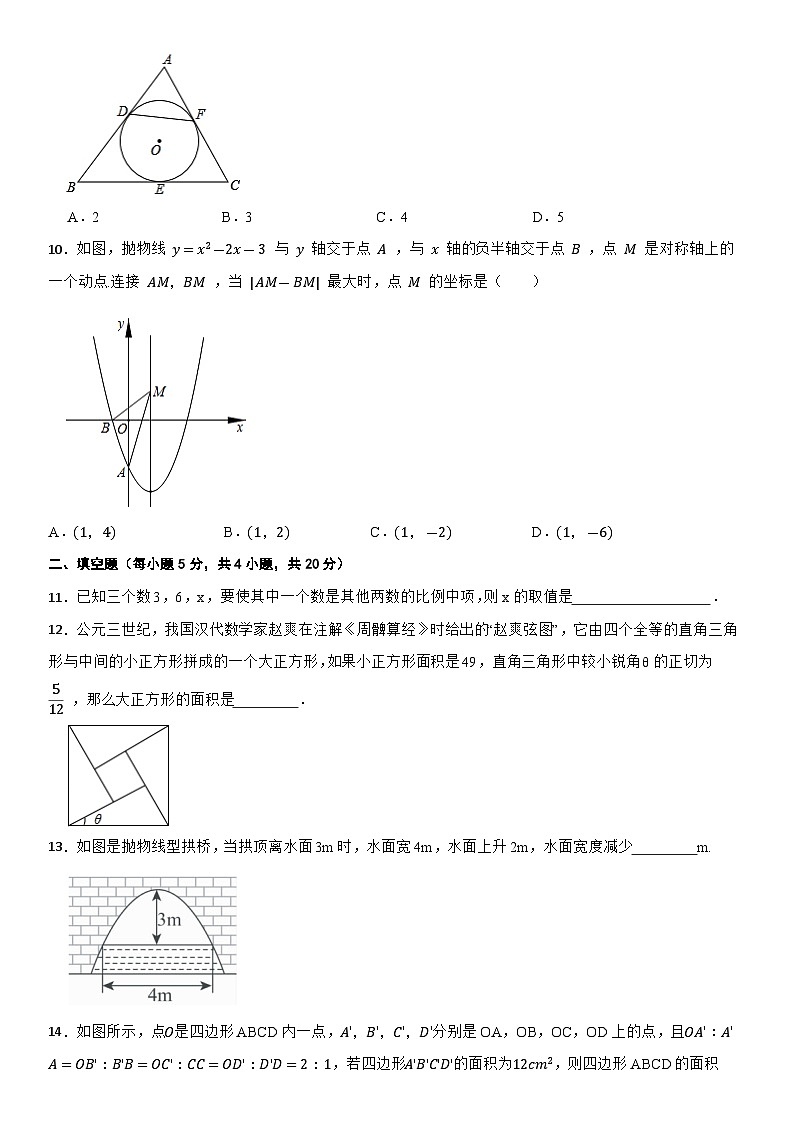
7．如图1，小球从左侧的斜坡滚下，到达底端后又沿着右侧斜坡向上滚，在这个过程中，小球的运动速度v（单位：m/s）与运动时间t （单位：s）的函数图象如图2，则该小球的运动路程y（单位：m）与运动时间t（单位：s）之间的函数图象大致是（ ）
A．B．
C．D．
8．在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）
A．（ 32 ，0）B．（2，0）C．（ 52 ，0）D．（3，0）
9．如图， △ABC 中， ∠A=60° ， BC=6 ，它的周长为 16. 若 ⊙O 与 BC ， AC ， AB 三边分别切于 E ， F ， D 点，则 DF 的长为（ ）
A．2B．3C．4D．5
10．如图，抛物线 y=x2-2x-3 与 y 轴交于点 A ，与 x 轴的负半轴交于点 B ，点 M 是对称轴上的一个动点.连接 AM，BM ，当 |AM-BM| 最大时，点 M 的坐标是（ ）
A．(1，4) B．(1，2) C．(1，-2) D．(1，-6)
二、填空题（每小题5分，共4小题，共20分）
11．已知三个数3，6，x，要使其中一个数是其他两数的比例中项，则x的取值是 ．
12．公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，如果小正方形面积是49，直角三角形中较小锐角θ的正切为 512 ，那么大正方形的面积是 ．
13．如图是抛物线型拱桥，当拱顶离水面3m时，水面宽4m，水面上升2m，水面宽度减少 m.
14．如图所示，点O是四边形ABCD内一点，A'，B'，C'，D'分别是OA，OB，OC，OD上的点，且OA'：A'A=OB'：B'B=OC'：CC=OD'：D'D=2：1，若四边形A'B'C'D'的面积为12cm2，则四边形ABCD的面积为 .
三、解答题（共9小题，15-18题每题8分，19-20题每题10分，21-22题每题12分，23题14分共90分。解答应写出文字说明、证明过程或演算步骤）
15．计算： (-12)2-54-(3-4)0+22sin60°
16．如图，∠1=∠2，∠B=∠D，AE=9，AD=12，AB=20．求AC的长度．
17．如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC.
（ 1 ）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1，（只画出图形）.
（ 2 ）作出△ABC关于原点O成中心对称的△A2B2C2，（只画出图形），写出B2和C2的坐标.
18．已知抛物线的顶点坐标为(2，1)且经过点(－1，－8).
（1）求抛物线的解析式；
（2）求出抛物线与坐标轴的交点坐标.
19．如图，在数学综合实践活动课上，两名同学要测量小河对岸大树BC的高度，甲同学在点A测得大树顶端B的仰角为45°，乙同学从A点出发沿斜坡走65米到达斜坡上点D，在此处测得树顶端点B的仰角为26.7°，且斜坡AF的坡度为1：2．
（1）求乙同学从点A到点D的过程中上升的高度；
（2）依据他们测量的数据求出大树BC的高度．（参考数据：sin26.7°≈0.45，cs26.7°≈0.89，tan26.7°≈0.50）
20．今年本市蜜桔大丰收，某水果商销售一种蜜桔，成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量 y （千克）与销售价 x （元/千克）之间的函数关系如图所示：
（1）求 y 与 x 之间的函数关系式；
（2）该经销商想要每天获得150元的销售利润，销售价应定为多少？
21．如图所示，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC．
（1）求证：DE是⊙O的切线；
（2）若∠C=30°，CD=10cm，求⊙O的半径．
22．如图1，抛物线y＝ax2+bx+3与x轴交于点A（3，0）、B（﹣1，0），与y轴交于点C，点P为x轴上方抛物线上的动点，点F为y轴上的动点，连接PA，PF，AF．
（1）求该抛物线所对应的函数解析式；
（2）如图1，当点F的坐标为（0，﹣3），过点P作x轴的垂线，交线段AF于点D，求线段PD长度的最大值；
（3）如图2，是否存在点F，使得△AFP是以点A为直角顶点的等腰直角三角形？若存在，求出点F的坐标；若不存在，请说明理由．
23．已知△ABC中，AB=AC=5，BC=8，E是射线BA上一点（不与点B重合），线段BE的垂直平分线与边BC交于点D.
（1）点E在边BA上，
①如图1，连接CE，如果CE平分∠ACB，求BD的长；
②如图2，射线DE交射线CA于点F，设BD=x，AF=y，求y关于x的的数解析式，并写出x的取值范围。
（2）如果△CDE是直角三角形，求BD的长
2023-2024年度合肥市庐阳区九年级上学期数学期末模拟卷一参考答案
1．【答案】A
2．【答案】B
3．【答案】D
4．【答案】B
5．【答案】D
6．【答案】B
7．【答案】C
8．【答案】C
9．【答案】A
10．【答案】D
11．【答案】32或12或±32
12．【答案】169
13．【答案】4-433
14．【答案】27cm2
15．【答案】解：原式 =14-36-1+22×32
=-34-26.
16．【答案】解：∵∠1=∠2，
∴∠1+∠BAE=∠2+∠BAE，
∴∠DAE=∠BAC，
∵∠B=∠D，
∴△DAE∽△BAC，
∴ADAB=AEAC，
∴1220=9AC，
∴AC=15．
17．【答案】解：（1）△A1B1C1如图所示；
（2）△A2B2C2如图所示，B2（4，-1），C2（1，-2）.
18．【答案】（1）解：设抛物线的解析式为y=a(x-2)2+1，
∵抛物线经过(-1，-8)，
∴-8=a(-1-2)2+1，
解得：a=-1，
∴y=-(x-2)2+1；
（2）解：令x=0得y=-3，
故与y轴交点为(0，-3)；
令y=0得-(x-2)2+1=0，
解得x1=1，x2=3，
∴与x轴交点为(1，0)或(3，0)．
19．【答案】（1）解：作DH⊥AE于H，如图所示：
在Rt△ADH中，∵DHAH=12，
∴AH＝2DH，
∵AH2+DH2＝AD2，
∴（2DH）2+DH2＝（65）2，
∴DH＝6（米）．
答：乙同学从点A到点D的过程中，他上升的高度为6米；
（2）解：如图所示：过点D作DG⊥BC于点G，
设BC＝x米，
在Rt△ABC中，∠BAC＝45°，
∴AC＝BC＝x，
由（1）得AH＝2DH＝12，
在矩形DGCH中，DH＝CG＝6，DG＝CH＝AH+AC＝x+12，
在Rt△BDG中，BG＝BC-CG＝BC-DH＝x-6，
∵tan∠BDG＝BGDG，
∴x-6x+12=tan26.7°≈0.5，
解得：x≈24，
答：大树的高度约为24米．
20．【答案】（1）解：设 y 与 x 之间的函数关系式 y=kx+b(k≠0) ，
把 (10,40) ， (18,24) 代入得： 10k+b=4018k+b=24 ，解得： k=-2b=60 ，
∴y 与 x 之间的函数关系式 y=-2x+60(10≤x≤18) ；
（2）解：根据题意得： (x-10)(-2x+60)=150 ，
整理得： x2-40x+375=0 ，
解得： x1=15 ， x2=25 （不合题意，舍去）.
答：该经销商想要每天获得150元的销售利润，销售价应定为15元.
21．【答案】（1）证明：连接OD，如图所示，
∵O是AB中点，D是BC中点，
∴OD∥AC，
∴∠DEA+∠ODE=180°，
又 ∵DE⊥AC，
∴∠ODE=90°，
∴OD⊥DE，
∴DE是⊙O的切线；
（2）解：连接AD，OD，如图所示，
∵AB是⊙O的直径，
∴∠BDA=∠ADC=90°，
∴△ADC是直角三角形，
∵∠C=30°，
∴AD=12AC，
∵CD=10cm，
∴在Rt△ADC中，AD2+CD2=4AD2，
∴AD=1003=1033．
∵OD∥AC，OB=OD，∠C=30°，
∴∠C=∠BDO=∠B=30°，
∴∠DOA=60°，
∵OD=OA，
∴△ODA为等边三角形．
∴OD=AD=1033（cm）．
∴⊙O的半径为1033（cm）．
22．【答案】（1）解：∵抛物线y＝ax2+bx+3与x轴交于点A（3，0）、B（﹣1，0），
∴9a+3b+3=0a-b+3=0，解得：a=-1b=2，
∴该抛物线所对应的函数解析式为y＝﹣x2+2x+3；
（2）解：如图1，过点P作PQ∥y轴交直线AF于点Q，
设直线AF的解析式为y＝kx+d，
由A（3，0），F（0，﹣3）的坐标得，直线AF的表达式为：y＝x﹣4，
设P（t，﹣t2+2t+3）（﹣1＜t＜3），则Q（t，t﹣4），
∴PQ＝﹣t2+2t+3﹣（t﹣4）＝﹣t2+t+7，
∴S△AFP＝12PQ•OA＝12（﹣t2+t+7）×3＝﹣32（t﹣12）2+878，
∵﹣32＜0，﹣1＜t＜3，
∴当t＝12时，△AFP面积的最大值为878；
（3）解：存在，理由：
设P（m，﹣m2+2m+3）（﹣1＜m＜3），F（0，n），
∵A（3，0），
∴OA＝3，OF＝|n|，
如图2，过点P作PD⊥x轴于点D，
则∠ADP＝90°＝∠AOF，
∴∠PAD+∠APD＝90°，
∵∠PAD+∠FAO＝90°，
∴∠APD＝∠FAO，
在△APD和△FAO中，
∠ADP=∠AOF∠APD=∠FAOAP=AF，
∴△APD≌△FAO（AAS），
∴PD＝OA，AD＝OF，
∵PD＝﹣m2+2m+3，AD＝3﹣m，
∴﹣m2+2m+3＝3，
解得：m＝0或2，
当m＝0时，P（0，3），AD＝3，
∴OF＝3，即|n|＝3，
∵点F在y的负半轴上，
∴n＝﹣3，
∴F（0，﹣3）；
当m＝2时，P（2，3），AD＝1，
∴OF＝1，即|n|＝1，
∵点F在y的负半轴上，
∴n＝﹣1，
∴F（0，﹣1）．
23．【答案】（1）解：①连接DE，在BC上截取CM=CA，连接EM，过A点作AN⊥BC于点N，
∴BN=12BC=4，
∴AN=AB2-BN2=52-42=3，
设BD=x，
∵线段BE的垂直平分线与边BC交于点D，
∴BD=DE=x，BG=GE=12BE，
∴∠B=∠BED，
∴∠EDC=2∠B，
∴∠BAC+∠B+∠C=∠BAC+2∠B=∠BAC+∠EDC=180°，
∵CE平分∠ACB，
∴∠BCE=∠ACE，
又∵AC=CM，CE=CE，
∴△ECA≌△ECM，
∴EA=EM，∠EAC=∠EMC，
∵∠EMC+∠EMD=180°
∴∠EMD=∠EDC，
∴EA=EM=ED=BD=x，
∴BE=5-x，
∴BG=GE=12BE=12(5-x)，
∵AN⊥BC，GD⊥BE，
∴∠BGD=∠BNA=90°，
又∵∠B=∠B，
∴△BDG∽△BAN，
∴BGBN=BDBA，即12(5-x)4=x5，
解得：x=2513，即BD=2513；
②过点E作EQ⊥BC于点Q，点F作FP⊥AB于点P，
由①得△BDG∽△BAN，
∴BGBN=BDBA=DGAN，即BG4=x5=DG3，
∴BG=GE=4x5，DG=3x5，
∴BE=8x5，
又∵EQ⊥BC，AN⊥BC，
∴∠EQB=∠ANB=90°，
∴△BEQ∽△BAN，
∴BEBA=EQMN=BQBN，即∴8x55=EQ3=BQ4，
∴EQ=2425x，BQ=3225x，
∴DQ=BQ-BD=3225x-x=725x，
又∵∠EDC=2∠B=∠B+∠C=∠FAP，
又∵FP⊥AB，
∴∠DQE=∠FPA=90°，
∴△DEQ∽△AFP，
∴FPEQ=FADE=APDQ，即FP2425x=yx=AP725x，
解得：FP=2425y，AP=725y，
又∵GD⊥BE，FP⊥AB，
∴∠DGE=∠FPE=90°，
又∵∠GED=∠PEF，
∴△DGE∽△FPE，
∴DGFP=EGEP，即3x52425y=4x5EP，
解得：EP=3225y，
又∵AB=BE+EP+PA，
∴8x5+3225y+725y=5，
即y=-4039x+12539，
∵点E在边BA上，
∴0<85x<5，
∴0∴x的取值范围为0（2）解：如图，过点E作EQ⊥BC于点Q，
根据②可得：BQ=3225x，EQ=2425x，
∴CQ=BC-BQ=8-3225x，
∴CE2=EQ2+CQ2=(2425x)2+(8-3225x)2，
当∠DEC=90°时，ED2+EC2=DC2，
即x2+(2425x)2+(8-3225x)2=(8-x)2，
解得：x1=0（舍去），x2=74，
当∠DCE=90°时，如图，
则∠B+∠BEC=∠BCA+∠ACE=90°，
∴∠BEC=∠ACE，
∴AC=AB=AE=5，
∴BE=10，
∴AC=BE2-BC2=102-82=6，
在Rt△CDE中，DE2=DC2+CE2，
即x2=(8-x)2+62，
解得：x=254，
综上所述，当BD的长为74或254时，△CDE是直角三角形．