
黑龙江省绥化市明水县2023-2024学年八年级上学期期末数学试题
展开
这是一份黑龙江省绥化市明水县2023-2024学年八年级上学期期末数学试题,共10页。试卷主要包含了考试时间为90分钟,下列说法中正确的是,计算 3的结果是等内容,欢迎下载使用。
考生注意:1.考试时间为90分钟
2. 全卷分选择题、填空题和解答题三道大题。总分为120分.
一、单项选择题(共12小题,请选择一个最佳答案,每小题3分,本题共计36分)
1.一个三角形的两边长为3和7,第三边长为偶数,则第三边为 ( )
A.6 B.6或8 C.4 D.4或6
B
2.在平面直角坐标系中,点 P3,−2关于 y轴的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
C
3.如图,一扇窗户打开后,用窗钩 BC可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性
B.两点之间线段最短
C.两点确定一条直线
D.垂线段最短
A
4.下列从左到右的变形,属于分解因式的是 ( )
A.a−3a+3=a2−9 B.x2+x−5=xx+1−5
C.a2+a=aa+1 D.x3y=x⋅x2⋅y
C
5.若分式 x2−42x−4值为零,则 x等于 ( )
A.0 B.2 C.±2 D.−2
C
6.已知 a+2+b−12=0则 a+b2013的值是( )
A.1 B.−1 C.2013 D.−2013
B
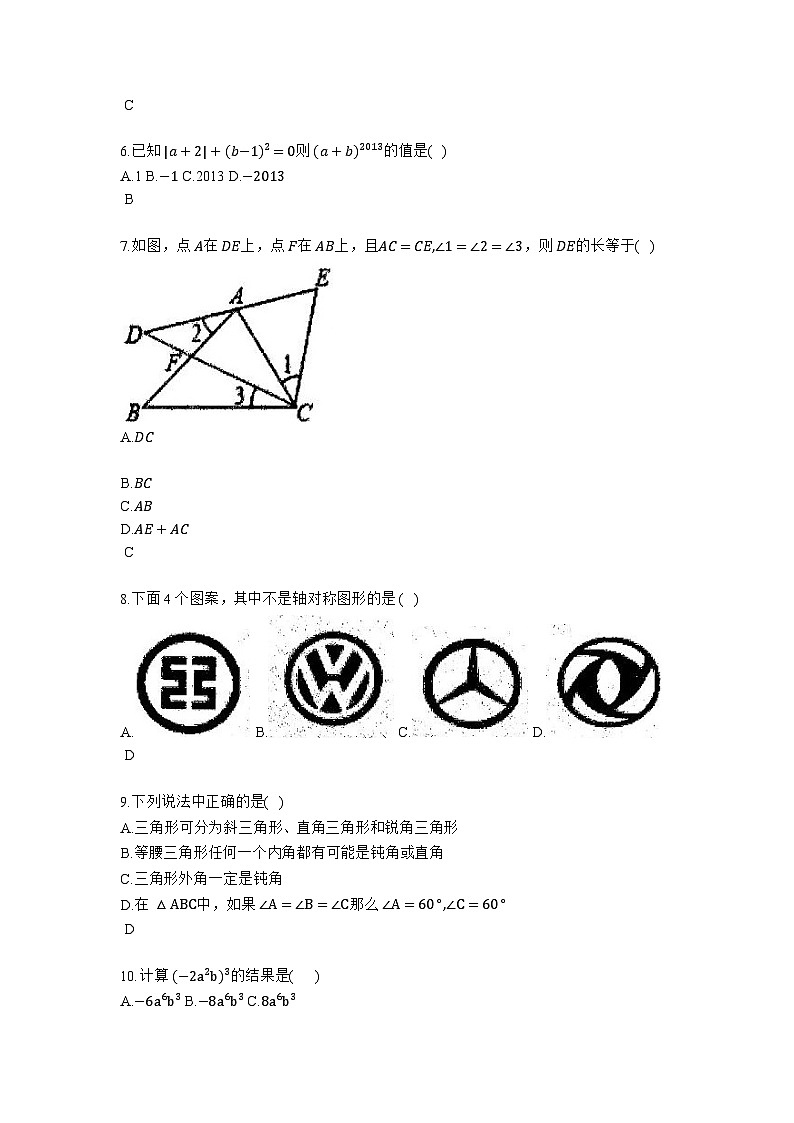
7.如图,点 A在 DE上,点 F在 AB上,且AC=CE,∠1=∠2=∠3,则 DE的长等于( )
A.DC
B.BC
C.AB
D.AE+AC
C
8.下面4个图案,其中不是轴对称图形的是 ( )
A. B. C. D.
D
9.下列说法中正确的是( )
A.三角形可分为斜三角形、直角三角形和锐角三角形
B.等腰三角形任何一个内角都有可能是钝角或直角
C.三角形外角一定是钝角
D.在 △ABC中,如果 ∠A=∠B=∠C那么 ∠A=60∘,∠C=60∘
D
10.计算 (−2a2b)3的结果是( )
A.−6a6b3 B.−8a6b3 C.8a6b3
D.−8a5b3
B
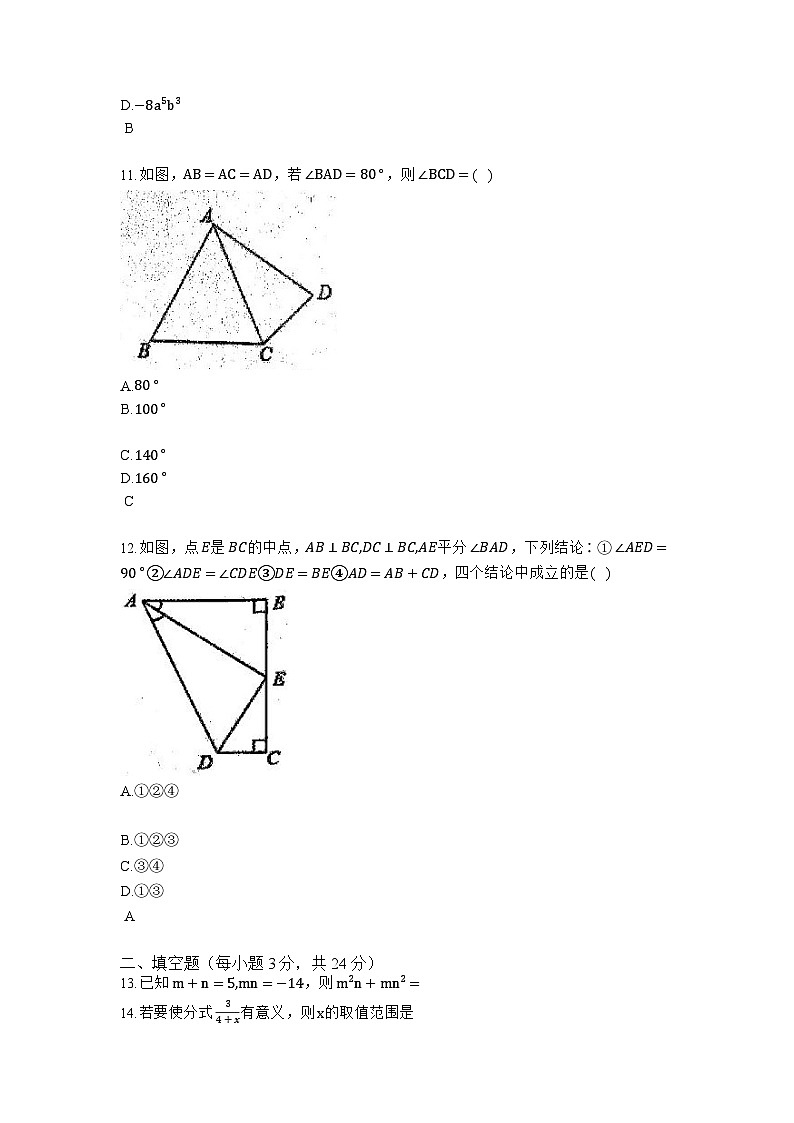
11.如图,AB=AC=AD,若 ∠BAD=80∘,则 ∠BCD=( )
A.80∘
B.100∘
C.140∘
D.160∘
C
12.如图,点 E是 BC的中点,AB⊥BC,DC⊥BC,AE平分 ∠BAD,下列结论∶① ∠AED=90∘②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是 ( )
A.①②④
B.①②③
C.③④
D.①③
A
二、填空题(每小题3分,共24分)
13.已知 m+n=5,mn=−14,则 m2n+mn2=
14.若要使分式 34+x有意义,则 x的取值范围是
15.如图,在 △ABC中,D是 BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使 DE=DF成立,你添加的条件是 .(不再添加辅助线和字母)
16.如图所示,已知 △ABC的周长是21,OB,OC别平分 ∠ABC和 ∠ACB,OD⊥BC于 D,且OD=3,则 △ABC的面积是 .
17.化简 x2−2xx2−4x+4结果是 .
18.已知关于 a−1x+2=1的分式方程=1无解,则 a= .
19.某县为治理污水,需要铺设一段全长为 300m的污水排放管道,铺设 120m后,为了尽量减少施工对城市交通所造成的影响,后来每天铺设管道的长度比原计划增加 20%,结果共用30天完成这一任务,求原计划每天铺设管道的长度如果设原计划每天铺设 xm管道,那么根据题意,可得方程 .
20.如图,已知点 P射线 ON上一动点(即 P可在射线 ON上运动),∠AON=30∘,当∠A= 时,△AOP为等腰三角形.
13. −7014.x≠−415.∠B=∠C(答案不唯一)−218.1
19.120x+300−1201+20%x=30(或 120x+1801.2x=30)20.30∘或 75∘或 120∘
三、解答题(共60分)
21.因式分解(每题3分,共6分)
①−xyz2+4xyz−4xy
②9m+n2−m−n2
21. ①−xy(z−2)2;;② 4(2m+n)m+2n
22.解方程(每小题4分,共8分)
①xx−3+2−x3−x=1
②1−xx−2=12−x−2
22.①xx−3+2−x3−x=1
去分母得,x−2−x=x−3,
去括号得,x−2+x=x−3,
移项合并同类项得,x=−1,
检验:当 x=−1时,x−3≠0,
故 x=−1是分式方程的根.
②方程两边同乘 x−2得,1−x=−1−2x−2
解得,x=2.
检验,当 x=2时,x−2=0,所以 x=2不是原方程的根,所以原分式方程无解
23.化简求值(6分)
已知 1x+1y=3,求 2x−xy+2yx−2xy+y的值.
23. 1x+1y=3,x+yxy=3,
x+y=3xy,
2x−xy+2yx−2xy+y=2x+y−xyx+y−2xy=6xy−xy3xy−2xy=5xyxy=5
24.(6分)如图,
(1)在网格中画出 △ABC关于 y轴对称的 △A1B1C1;
(2)写出 △ABC关于 x轴对称的 △A2B2C2的各项点坐标;
(3)在 y轴上确定一点 P,使 △PAB周长最短. (只需作图,保留作图痕迹)
24.(1)略;(2)A2−3,−2,B2−4,3,C2−1,1
(3)连结 AB1或 BA1交 y轴于点 P,则点 P即为所求
25.(6分)已知等边三角形 ABC,延长 BA至 E,延长 BC至 D,使得 AE=BD.
求证:EC=ED
25.证明:延长 BD到 F,使 BF=BE,连接 EF. 则 BF−BC=BE−BA.
即 CF=AE;又 AE=BD.
故 CF=BD,DF=BC.
∵∠B=60∘.
∴△BEF为等边三角形,BE=EF;∠B=∠F=60∘
∴△EB≅△EFDSAS,
EC=ED.
26.(8分)千年古镇赵化开发的鑫城小区的内坝是一块长为 (3a+b)米,宽为 2a+b米的长方形地,物业部门计划将内坝进行绿化(如图阴影部分),中间部分将修建一仿古小景点(如图中间的长方形),则绿化的面积是多少平方米?并求出当 a=3,b=2时的绿化面积.
26.解:由题意,得
3a+b2a+b−a+b2=6a2+5ab+b2−a2−2ab−b2=5a2+3ab,
当 a=3,b=2时,5a2+3ab=5×32+3×3×2=63,
答:绿化的面积是 5a2+3ab平方米,
当 a=3,b=2时的绿化面积是 63m2.
27.(8分)某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
27.(1)解:设第一批购进书包的单价是 x元,则第二批购进书包的单价是 x+4元
∴6300x+4=3×2000x
解得 x=80
经检验:x=80是原分式方程的解
∴一批购进书包的单价是80元
(2)第一批购进书包的数量是:2000÷80=25个
第一批购进书包的数量是:6300÷84=75个
∴店共盈利:120×25+75−2000−3600=3700
答:第一批购进书包的单价是80元,商店共盈利3700元
28.(12分)在 △ABC中,BC=AC,∠BCA=90°,P为直线 AC上一点,过点 A作 AD⊥BP于点 D,交直线 BC于点 Q.
(1)如图1,当 P在线段 AC上时,求证:BP=AQ;
(2)如图2,当 P在线段 CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在 (2)的条件下,当 ∠DBA= 时,存在 AQ=2BD,说明理由.
28.(1)证明:∵BF=CE,
∴BF+FC=CE+FC,
即 BC=EF,
∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90∘,
在 △ABC和 △DEF中, {AB=DE∠B=∠E=90∘BC=EF,
∴△ABC≅△DEFSAS;
(1)【小问1详解】
解:证明:∵∠ACB=∠ADB=90∘,∠APD=∠BPC,
∴∠DAP=∠CBP,
在 △ACQ和 △BCP中
∵{∠QCA=∠PCBCA=CB∠CAQ=∠CBP
. ∴△ACQ≅△BCPASA,
∴BP=AQ;
(2)成立
(2)【小问2详解】
成立,理由如下:
延长 BA交 PQ于 H,
∵∠ACQ=∠BDQ=90∘,∠AQC=∠BQD,
∴∠CAQ=∠PBC,
在 △AQC和 △BPC中,
∠ACQ=∠BCP
CA−CB
∠CAQ=∠PBC
∴△AQC≅△BPCASA,
∴AQ=BP,
故答案为:成立;
(3)22.5∘
(3)【小问3详解】
解:当 ∠DBA=22.5∘时,存在 AQ=2BD,理由如下
∵∠BAC=∠DBA+∠APB=45∘,
∴∠PBA=∠APB=22.5∘,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
∵△PBC≅△QAC,,
∴AQ=PB,
∴AQ=2BD.
故答案为:22.5∘
相关试卷
这是一份黑龙江省绥化市明水县2023-2024学年八年级上学期期末数学试题(含解析),共18页。试卷主要包含了5 毫米黑色墨水签字等内容,欢迎下载使用。
这是一份黑龙江省绥化市明水县2023-2024学年七年级上学期1月期末数学试题,共9页。
这是一份黑龙江省绥化市明水县2023-2024学年九年级上学期期末数学试题,共11页。试卷主要包含了考试时间为90分钟,下列说法正确的是等内容,欢迎下载使用。









