微专题14　折叠与探索问题

这是一份微专题14　折叠与探索问题，共7页。
1.(2019·全国Ⅲ卷)图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB＝1，BE＝BF＝2，∠FBC＝60°.将其沿AB，BC折起使得BE与BF重合，连接DG，如图2.
(1)证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；
(2)求图2中的平面BCG与平面CGA夹角的大小.
2.(2021·全国甲卷)已知直三棱柱ABC－A1B1C1中，侧面AA1B1B为正方形，AB＝BC＝2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1.
(1)证明：BF⊥DE；
(2)当B1D为何值时，平面BB1C1C与平面DFE所成的二面角的正弦值最小？
【热点突破】
热点一 折叠问题
解答折叠问题的关键是分清翻折前后图形的位置和数量关系的变与不变，一般地，位于“折痕”同侧的点、线、面之间的位置和数量关系不变，而位于“折痕”两侧的点、线、面之间的位置关系会发生变化；对于不变的关系应在平面图形中处理，而对于变化的关系则要在立体图形中解决.
考向1 折叠后的位置关系及空间角
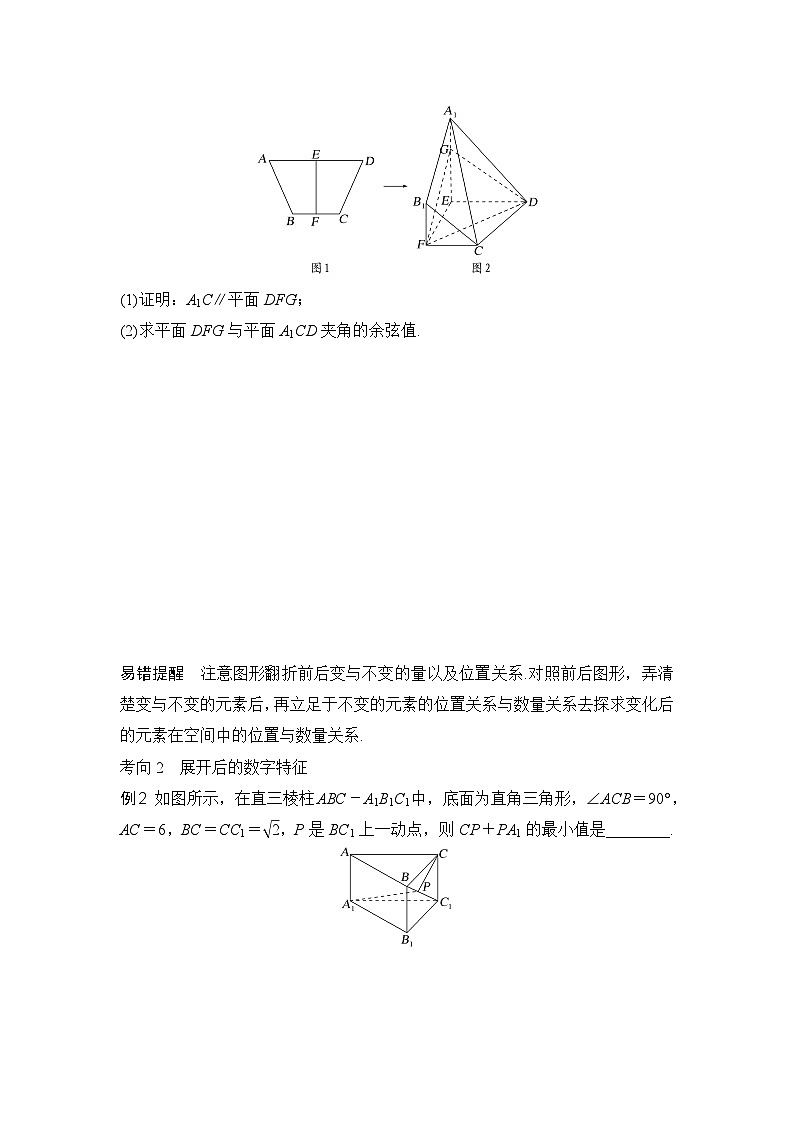
例1 (2023·邯郸模拟)如图1，四边形ABCD是等腰梯形，E，F分别是AD，BC的中点，AD＝2BC＝2EF＝4.将四边形ABFE沿着EF折起到四边形A1B1FE处，使得A1C＝3，如图2，G在A1E上，且eq \(A1E,\s\up6(→))＝3eq \(A1G,\s\up6(→)).
(1)证明：A1C∥平面DFG；
(2)求平面DFG与平面A1CD夹角的余弦值.
易错提醒 注意图形翻折前后变与不变的量以及位置关系.对照前后图形，弄清楚变与不变的元素后，再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.
考向2 展开后的数字特征
例2 如图所示，在直三棱柱ABC－A1B1C1中，底面为直角三角形，∠ACB＝90°，AC＝6，BC＝CC1＝eq \r(2)，P是BC1上一动点，则CP＋PA1的最小值是________.
易错提醒 几何体表面上的最短距离要注意棱柱的侧面展开图可能有多种，如长方体的表面展开图等，要把不同展开图中的最短距离进行比较，找出其中的最小值.
训练1 如图1，在直角梯形ABCD中，AB∥DC，∠D＝90°，AB＝2，DC＝3，AD＝eq \r(3)，CE＝2ED.沿BE将△BCE折起，使点C到达点C1的位置，且AC1＝eq \r(6)，如图2.
(1)求证：平面BC1E⊥平面ABED；
(2)求直线BC1与平面AC1D所成角的正弦值.
热点二 探索问题
与空间向量有关的探索性问题主要有两类：一类是探索线面的位置关系；另一类是探索线面角或平面与平面的夹角满足特定要求时的存在性问题.解题思路：先建立空间直角坐标系，引入参数(有些是题中已给出)，设出关键点的坐标，然后探索这样的点是否存在，或参数是否满足要求，从而作出判断.
考向1 探索线面位置关系
例3 (2023·成都诊断)如图，在正四棱柱ABCD－A1B1C1D1中，AA1＝2AB＝2，E，F分别为棱AA1，CC1的中点，G为棱DD1上的动点.
(1)求证：B，E，D1，F四点共面；
(2)是否存在点G，使得平面GEF⊥平面BEF？若存在，求出DG的长；若不存在，说明理由.
考向2 与空间角有关的探索性问题
例4 (2023·石家庄模拟)如图，四棱锥S－ABCD中，底面ABCD为矩形，且垂直于侧面SAB，O为AB的中点，SA＝SB＝AB＝2，AD＝eq \r(2).
(1)证明：BD⊥平面SOC；
(2)侧棱SD上是否存在点E，使得平面ABE与平面SCD夹角的余弦值为eq \f(1,5)，若存在，求eq \f(SE,SD)的值；若不存在，说明理由.
规律方法 解决立体几何探索性问题的基本方法
(1)通常假设问题中的数学对象存在或结论成立，再在这个前提下进行推理，如果能推出与条件吻合的数据或事实，说明假设成立，并可进一步证明，否则假设不成立.
(2)探索线段上是否存在满足条件的点时，一定要注意三点共线的应用.
训练2 (2023·厦门质检)在三棱柱ABC－A1B1C1中，四边形AA1B1B是菱形，AB⊥AC，平面AA1B1B⊥平面ABC，平面A1B1C1与平面AB1C的交线为l.
(1)证明：A1B⊥B1C.
(2)已知∠ABB1＝60°，AB＝AC＝2，l上是否存在点P，使A1B与平面ABP所成角为30°？若存在，求B1P的长度；若不存在，请说明理由.