第一章平行线（浙教版-中考真题精选）-浙江省2023-2024学年七年级下学期期末数学提高练习

这是一份第一章平行线（浙教版-中考真题精选）-浙江省2023-2024学年七年级下学期期末数学提高练习，共12页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。
一、单选题
1．（2023·浙江金华·统考中考真题）如图，已知，则的度数是（ ）

A．B．C．D．
2．（2022·浙江台州·统考中考真题）如图，已知，为保证两条铁轨平行，添加的下列条件中，正确的是（ ）
A．B．C．D．
3．（2022·浙江湖州·统考中考真题）如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（ ）
A．2cmB．3cmC．4cmD．5cm
4．（2022·浙江绍兴·统考中考真题）如图，把一块三角板的直角顶点B放在直线上，，ACEF，则（ ）
A．30°B．45°
C．60°D．75°
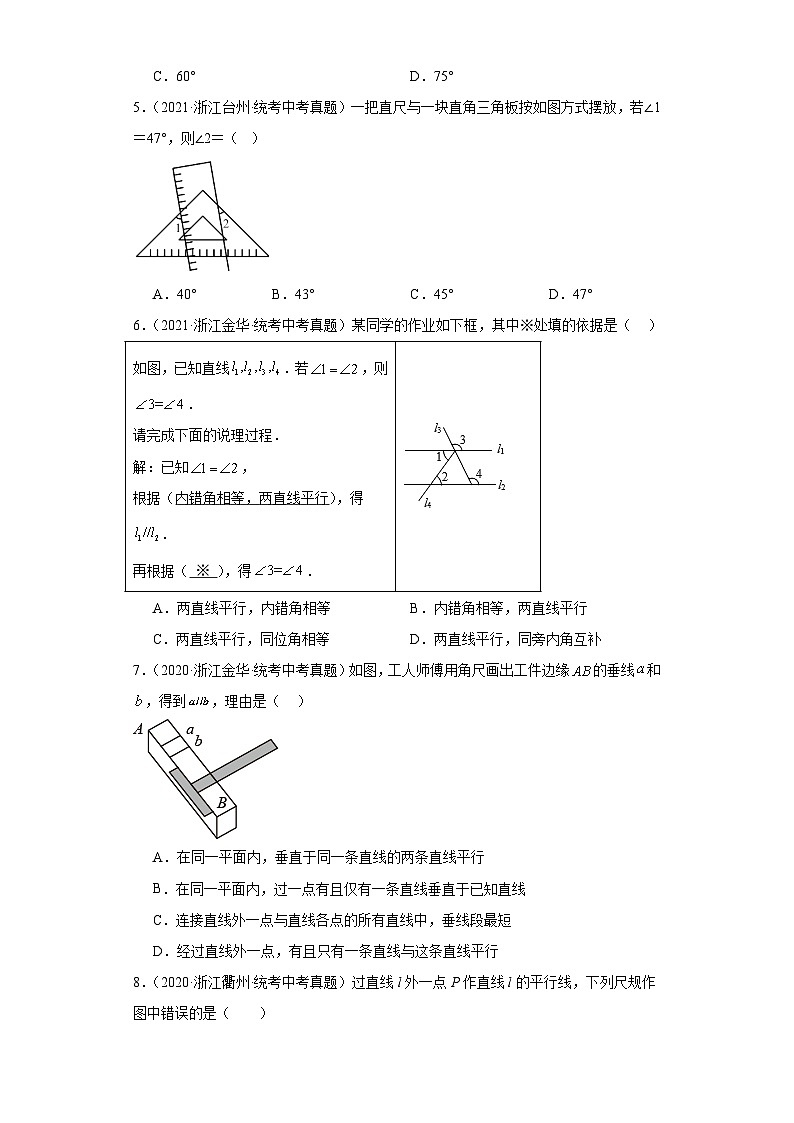
5．（2021·浙江台州·统考中考真题）一把直尺与一块直角三角板按如图方式摆放，若∠1＝47°，则∠2＝（ ）
A．40°B．43°C．45°D．47°
6．（2021·浙江金华·统考中考真题）某同学的作业如下框，其中※处填的依据是（ ）
A．两直线平行，内错角相等B．内错角相等，两直线平行
C．两直线平行，同位角相等D．两直线平行，同旁内角互补
7．（2020·浙江金华·统考中考真题）如图，工人师傅用角尺画出工件边缘的垂线和，得到，理由是（ ）
A．在同一平面内，垂直于同一条直线的两条直线平行
B．在同一平面内，过一点有且仅有一条直线垂直于已知直线
C．连接直线外一点与直线各点的所有直线中，垂线段最短
D．经过直线外一点，有且只有一条直线与这条直线平行
8．（2020·浙江衢州·统考中考真题）过直线l外一点P作直线l的平行线，下列尺规作图中错误的是（ ）
A．B．
C．D．
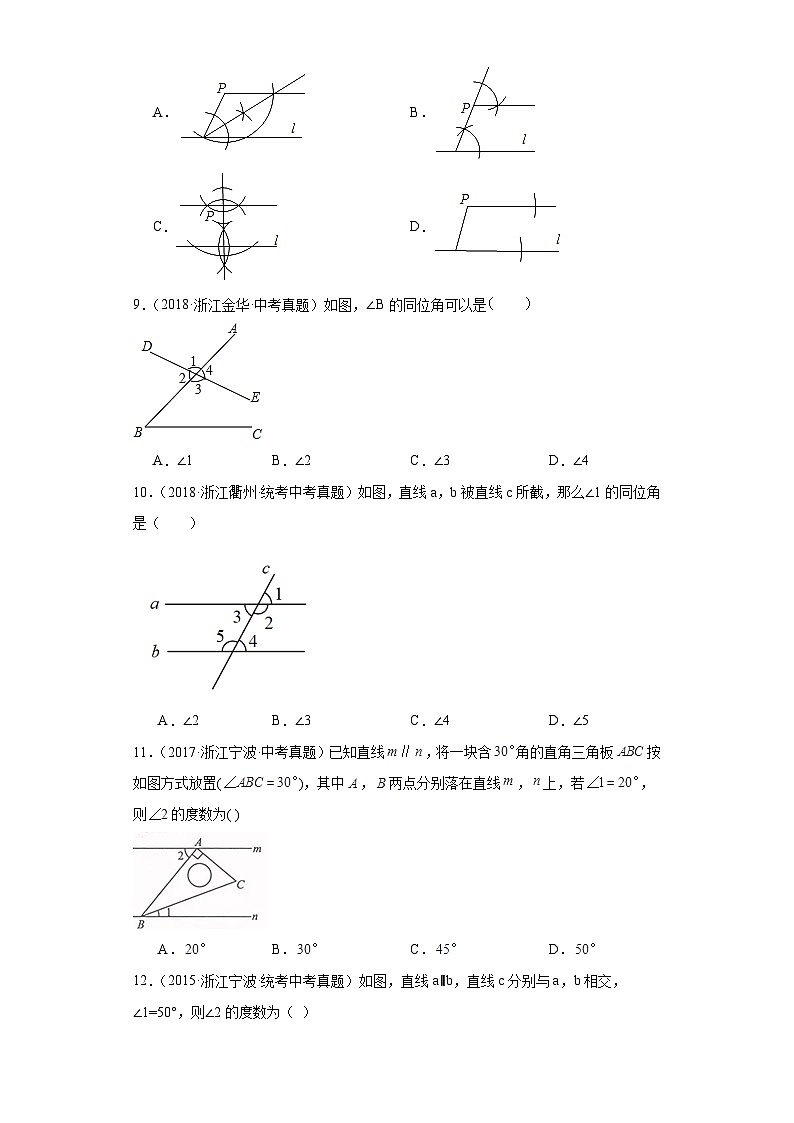
9．（2018·浙江金华·中考真题）如图，∠B的同位角可以是
A．∠1B．∠2C．∠3D．∠4
10．（2018·浙江衢州·统考中考真题）如图，直线a，b被直线c所截，那么∠1的同位角是（ ）
A．∠2B．∠3C．∠4D．∠5
11．（2017·浙江宁波·中考真题）已知直线，将一块含角的直角三角板按如图方式放置()，其中，两点分别落在直线，上，若，则的度数为( )
A．B．C．D．
12．（2015·浙江宁波·统考中考真题）如图，直线a∥b，直线c分别与a，b相交，∠1=50°，则∠2的度数为（ ）
A．150°B．130°C．100°D．50°
二、填空题
13．（2023·浙江台州·统考中考真题）用一张等宽的纸条折成如图所示的图案，若，则∠2的度数为 ．

14．（2017·浙江台州·中考真题）如图，已知直线，则∠2= ．
15．（2017·浙江金华·统考中考真题）如图，已知，直线与相交于两点，把一块含角的三角尺按如图位置摆放若，则 ．
16．（2016·浙江湖州·中考真题）如图 1 是我们常用的折叠式小刀，图 2 中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图 2 所示的∠1 与∠2 ，则∠1 与∠2 的度数和是 度．
17．（2015·浙江杭州·统考中考真题）如图，点 A，C，F，B 在同一直线上，CD 平分∠ECB，FG//CD．若∠ECA 为 α 度，则∠GFB为 度（用关于 α 的代数式表示）．
如图，已知直线．若，则．
请完成下面的说理过程．
解：已知，
根据（内错角相等，两直线平行），得．
再根据（ ※ ），得．
参考答案：
1．C
【分析】由可得，可得，再利用邻补角的含义可得答案．
【详解】解：如图，标记角，

∵，
∴，而，
∴，
∴；
故选C
【点睛】本题考查的是平行线的判定与性质，邻补角的含义，熟记平行线的判定与性质是解本题的关键．
2．C
【分析】根据平行线的判定方法进行判断即可．
【详解】解：A.∠1与∠2是邻补角，无法判断两条铁轨平行，故此选项不符合题意；
B. ∠1与∠3与两条铁轨平行没有关系，故此选项不符合题意；
C. ∠1与∠4是同位角，且∠1=∠4=90°，故两条铁轨平行，所以该选项正确；
D. ∠1与∠5与两条铁轨平行没有关系，故此选项不符合题意；
故选：C．
【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定是解答本题的关键．
3．C
【分析】据平移的性质可得BB′=CC′=1，列式计算即可得解．
【详解】解：∵△ABC沿BC方向平移1cm得到△A′B′C′，
∴BB′=CC′=1cm，
∵B′C=2cm，
∴BC′= BB′+ B′C+CC′=1+2+1=4（cm）．
故选：C．
【点睛】本题考查了平移的性质，熟记性质得到相等的线段是解题的关键．
4．C
【分析】根据三角板的角度，可得，根据平行线的性质即可求解．
【详解】解：，
ACEF，
故选C
【点睛】本题考查了平行线的性质，掌握平行线的性质是解题的关键．
5．B
【分析】过三角板的直角顶点作直尺两边的平行线，根据平行线的性质即可求解．
【详解】解：如图，过三角板的直角顶点作直尺两边的平行线，
∵直尺的两边互相平行，
∴，
∴，
∴，
故选：B．
【点睛】本题考查平行线的性质，掌握平行线的性质是解题的关键．
6．C
【分析】首先准确分析题目，已知，结论是，所以应用的是平行线的性质定理，从图中得知∠3和∠4是同位角关系，即可选出答案．
【详解】解：∵，
∴（两直线平行，同位角相等）．
故选C．
【点睛】本题主要考查了平行线的性质的应用，解题的关键是理解平行线之间内错角的位置，从而准确地选择出平行线的性质定理．
7．A
【分析】根据在同一平面内，垂直于同一条直线的两条直线平行判断即可．
【详解】解：由题意得：
∴a∥b（在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行），
故选：A．
【点睛】本题考查平行线的判定，平行公理，解题关键是理解题意，灵活运用所学直线解决问题．
8．D
【分析】根据平行线的判定方法一一判断即可．
【详解】A、由作图可知，内错角相等两直线平行，本选项不符合题意．
B、由作图可知，同位角相等两直线平行，本选项不符合题意．
C、与作图可知，垂直于同一条直线的两条直线平行，本选项不符合题意，
D、无法判断两直线平行，
故选：D．
【点睛】本题考查作图-复杂作图，平行线的判定等知识，解题的关键是读懂图象信息，属于中考常考题型．
9．D
【分析】直接利用两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角，进而得出答案．
【详解】∠B的同位角可以是：∠4．
故选D．
【点睛】此题主要考查了同位角的定义，正确把握定义是解题关键．
10．C
【详解】分析：根据同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角解答即可．
详解：由同位角的定义可知，∠1的同位角是∠4．
故选C．
点睛：本题考查了同位角问题，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解．
11．D
【详解】试题解析：如图，
∵
∴∠2=∠3+∠1
∵∠1=20°，∠3=30°
∴∠2=50°
故选D.
考点：平行线的性质．
12．B
【详解】试题分析：如图所示，∵a∥b，∠1=50°，∴∠3=∠1=50°，∵∠2+∠3=180°，∴∠2=130°．故选B．
考点：平行线的性质．
13．/度
【分析】如图，先标注点与角，由对折可得：，求解，利用，从而可得答案．
【详解】解：如图，先标注点与角，

由对折可得：，
∴，
∵，
∴；
故答案为：
【点睛】本题考查的是折叠的性质，平行线的性质，熟记两直线平行，同位角相等是解本题的关键．
14．110°
【详解】解：根据a∥b得∠1=∠3=70°，
∵∠2+∠3=180°，
∴∠2=180°-70°=110°．
故答案为110°．
15．20°.
【详解】试题分析：已知∠1=130°，根据对顶角的性质可得∠DCM=130°，已知，根据平行线的性质可得
∠MCD+∠BDC=180°，所以∠BDC=50°，又因∠BDA=30°，即可得∠2=50°-30°=20°.
16．90．
【详解】试题分析：如图2，AB∥CD，∠AEC=90°，作EF∥AB，根据平行线的传递性得到EF∥CD，则根据平行线的性质得∠1=∠AEF，∠2=∠CEF，所以∠1+∠2=∠AEC=90°
如图2，AB∥CD，∠AEC=90°， 作EF∥AB，则EF∥CD， 所以∠1=∠AEF，∠2=∠CEF，
所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°
考点：平行线的性质
17．90°﹣
【详解】∵∠ECA=，
∴∠ECB=180°-，
∵CD平分∠ECB，
∴∠DCB=∠ECB=（180°-）=90°-，
又∵FG//CD
∴∠GFB=∠DCB=90°-．