广东省深圳市福田区九校联考2023-2024学年九年级上学期月考历史试题

这是一份广东省深圳市福田区九校联考2023-2024学年九年级上学期月考历史试题，共10页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1．设集合，则（ ）
A．B．C．D．
2．已知复数，则在复平面上对应的点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．已知，则（ ）
A．B．C．D．
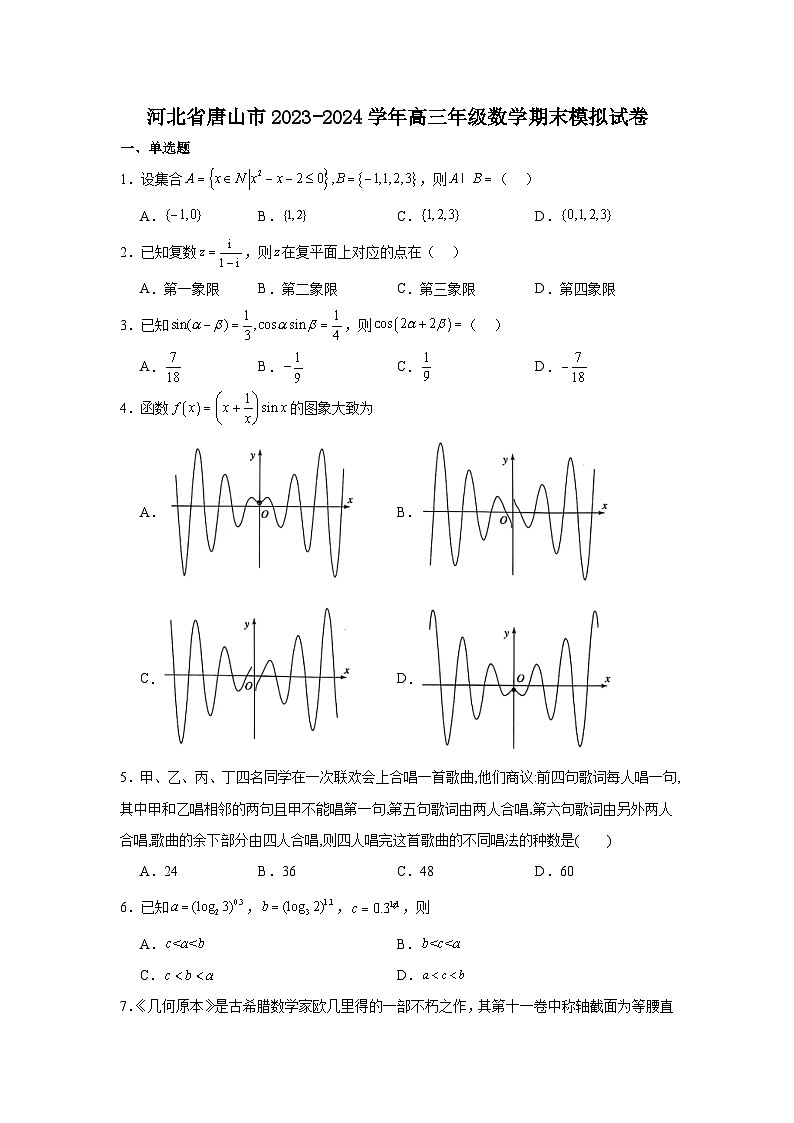
4．函数的图象大致为
A．B．
C．D．
5．甲、乙、丙、丁四名同学在一次联欢会上合唱一首歌曲,他们商议:前四句歌词每人唱一句,其中甲和乙唱相邻的两句且甲不能唱第一句,第五句歌词由两人合唱,第六句歌词由另外两人合唱,歌曲的余下部分由四人合唱,则四人唱完这首歌曲的不同唱法的种数是( )
A．24B．36C．48D．60
6．已知，，，则
A．B．
C．D．
7．《几何原本》是古希腊数学家欧几里得的一部不朽之作，其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为，则它的体积为更多课件教案等优质滋元可 家 威杏 MXSJ663 （ ）
A．B．C．D．
8．已知函数f（x）＝ ，若∃x1，x2∈R，且x1≠x2，使得f（x1）＝f（x2），则实数a的取值范围是（ ）
A．[2，3]∪（﹣∞，﹣5]B．（﹣∞，2）∪（3，5）
C．[2，3]D．[5，+∞）
二、多选题
9．已知函数，则下列说法正确的是为（ ）
A．的图像关于原点对称B．
C．的值域为D．，且，则恒成立
10．已知点，动点满足，则下面结论正确的为（ ）
A．点的轨迹方程为B．点到原点的距离的最大值为5
C．面积的最大值为4D．的最大值为18
11．已知函数（，，），满足：，恒成立，且在上有且仅有2个零点，则（ ）
A．，
B．函数的单调递增区间为
C．函数的对称中心为
D．函数的对称轴为直线，
12．已知椭圆的左、右焦点分别为、，点、在上，，，则（ ）
A．B．的离心率为
C．的短轴长为D．的面积为
三、填空题
13．已知是平面单位向量，且，若平面向量满足，则 ．
14．定长是3的线段AB的两端点在抛物线上移动，M是线段AB的中点，则M到y轴距离的最小值是 .
15．如图，长方体中，，点在线段上，且为线段的中点，若，则异面直线与所成角的余弦值为 ．
16．已知，，，，，，例如，则，，，．若，则 ．
四、解答题
17．已知数列满足，且.
（1）求数列的通项公式；
（2）若数列满足，求数列的前项和.
18．在中，内角所对的边分别为，设满足条件和，
(1)求角和；
(2)若，求的面积；
(3)求．
19．1.某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖，每次抽奖都是从装有4个红球，6个白球的甲箱和装有5个红球､5个白球的乙箱中，各随机摸出1个球，若都是红球，则可获得现金50元；若只有1个红球，则可获得20元购物券；若没有红球，则不获奖.
(1)若某顾客有1次抽奖机会，求该顾客获得现金或购物券的概率；
(2)若某顾客有3次抽奖机会，记该顾客在3次抽奖中获得现金为X元，求X的分布列和数学期望.
20．如图，在三棱锥中，平面，已知，点分别为的中点.
（1）求证：；
（2）若F在线段上，满足平面，求的值；
（3）若三角形是正三角形，边长为2，求二面角的正切值.
21．已知双曲线：，其渐近线方程为，点在上.
(1)求双曲线的方程；
(2)过点的两条直线AP，AQ分别与双曲线交于P，Q两点（不与点A重合），且两条直线的斜率之和为1，求证：直线PQ过定点.
22．已知函数，曲线在点处的切线与轴平行.
（Ⅰ）求的值；
（Ⅱ）若，求函数的最小值；
（Ⅲ）求证：存在，当时， ．
答案
1．B
2．B
3．D
4．A
5．D
6．B
7．B
8．B
9．AC
10．ABD
11．BCD
12．ABD
13．
14．
15．
16．0
17．（1）
从而有：，…………
叠加可得：，
又满足等式，从而
（2），①
②
①-②得：
即有：.
18．（1）由余弦定理得，
因为，所以．
由已知条件，应用正弦定理
，
即，
所以．
（2）因为，所以，
所以．
（3）因为，
所以，又，
所以，
所以．
因为，
所以．
19．（1）根据题意，取出的小球没有白球，即获得现金或购物券的概率为.
（2）X的所有可能取值为150，100，50，0，
一次抽奖抽到两次均为红球的概率为，其他情况概率为，
∴，，
，.
∴X的分布列如下：
∴X的数学期望为：.
20．（1）因为平面，平面，所以，
又因为，是的中点，所以，
而、是平面内的相交直线，所以平面，
而平面，所以.
（2）连结，交于点，连结、
因为平面，平面，平面平面，
所以，
已知、分别是、的中点，则为的中位线，
因此，，可得，
所以，即的值为．
（3）因为是正三角形，边长为2，则，
过点作交的中点，，
又因为平面，所以，
则且，
所以，即是等腰三角形，
连接，有，
所以二面角为，
又因为，所以在中，
，
所以二面角的正切值为.
21.（1）∵，，依题意，
解得：，，
所以双曲线C的方程为
（2）依题意可知斜率存在，设方程为，，，
则，即①，
所以
设直线AP，AQ的斜率分别为，，由题意知：，故有：
，
整理得
当，，过舍去，
当，，过点，
此时，将代入①得，得，满足题意.
∴直线PQ过定点
22．（Ⅰ），
由已知可得，所以，得．
（Ⅱ），令，得，
所以，，的变化情况如表所示：
所以的最小值为．
（Ⅲ）证明：显然，且，
由（Ⅱ）知，在上单调递减，在上单调递增．
又，，
由零点存在性定理，存在唯一实数，满足，
即，，
综上，存在两个零点，分别为，．
所以时，，即，在上单调递增；
时，，即，在上单调递减；
时，，即，在上单调递增，
所以是极大值，是极小值，
，
因为，，
所以，所以，
因此时，．
因为且在上单调递增，
所以一定存在满足，
所以存在，当时，.X
150
100
50
0
P
极小值