四川省自贡市2023-2024学年数学八上期末统考模拟试题含答案

这是一份四川省自贡市2023-2024学年数学八上期末统考模拟试题含答案，共8页。试卷主要包含了立方根等于本身的数是，下列各数是无理数的是，一次函数等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．如图，在直角△ABC中，，AB=AC，点D为BC中点，直角绕点D旋转，DM，DN分别与边AB，AC交于E，F两点，下列结论：①△DEF是等腰直角三角形；② AE=CF；③△BDE≌△ADF；④ BE+CF=EF，其中正确结论是（ ）
A．①②④B．②③④C．①②③D．①②③④
2．下列根式中，最简二次根式是（ ）
A．B．C．D．
3．如图，给正五边形的顶点依次编号为1，2，3，4，1．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”，如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→1→1为第一次“移位”，这时他到达编号为1的顶点，然后从1→2为第二次“移位”．若小宇从编号为4的顶点开始，第2020次“移位”后，则他所处顶点的编号为（ ）．
A．2B．3C．4D．1
4．已知a，b，c是三角形的三边，如果满足（a﹣3）2++|c﹣5|=0，则三角形的形状是（ ）
A．底与腰部相等的等腰三角形B．等边三角形
C．钝角三角形D．直角三角形
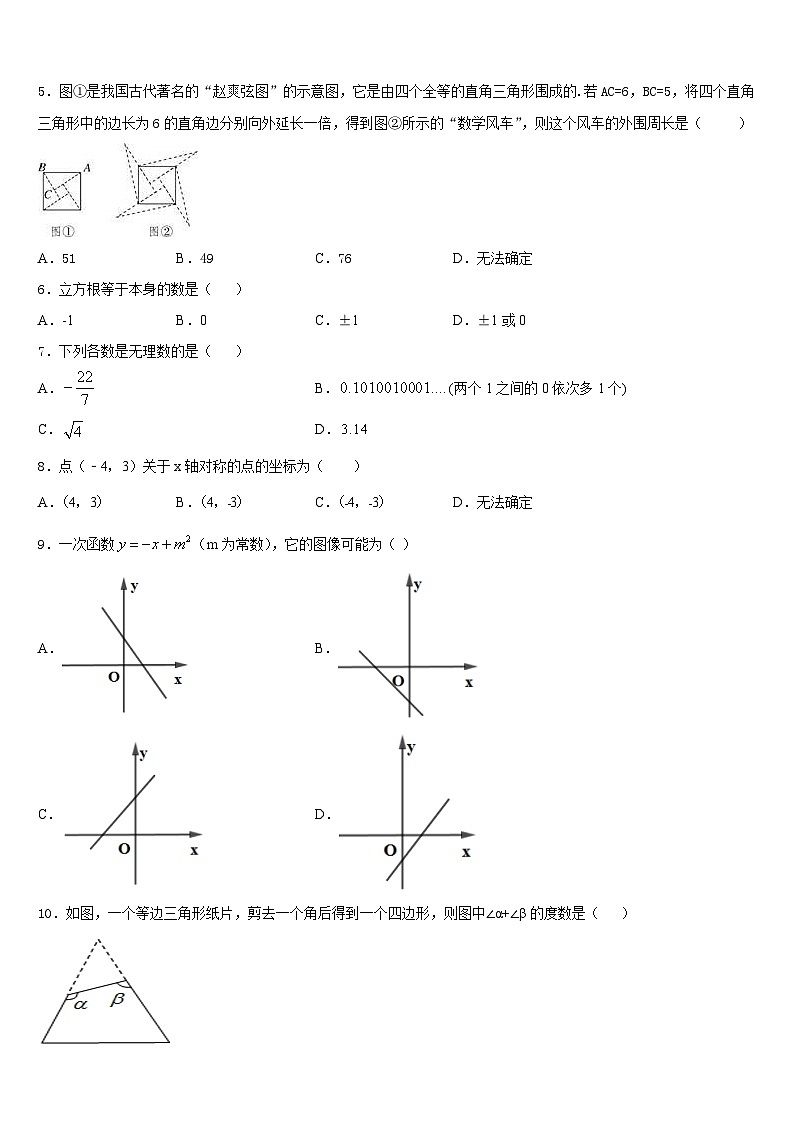
5．图①是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的.若AC=6，BC=5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图②所示的“数学风车”，则这个风车的外围周长是（ ）
A．51B．49C．76D．无法确定
6．立方根等于本身的数是（ ）
A．-1B．0C．±1D．±1或0
7．下列各数是无理数的是（ ）
A．B．(两个1之间的0依次多1个)
C．D．
8．点（﹣4，3）关于x轴对称的点的坐标为（ ）
A．（4，3）B．（4，﹣3）C．（﹣4，﹣3）D．无法确定
9．一次函数（m为常数），它的图像可能为（ ）
A．B．
C．D．
10．如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．要使在实数范围内有意义，x应满足的条件是_____．
12．当x_________时，分式分式有意义
13．已知一次函数，若y随x的增大而减小，则的取值范围是___．
14．已知,则的值为________．
15．已知，那么以边边长的直角三角形的面积为__________．
16．若+（y﹣1）2＝0，则（x+y）2020＝_____．
17．在平面直角坐标系中，将点（-b，-a）称为点（a，b）的“关联点”（例如点（-2，-1）是点（1，2）的“关联点”）．如果一个点和它的“关联点”在同一象限内，那么这一点在第_______象限．
18．下列各式：①；②；③；
④.其中计算正确的有__________（填序号即可）．
三、解答题(共66分)
19．（10分）从沈阳到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是千米，普通列车的行驶路程是高铁的行驶路程的倍．
（1）求普通列车的行驶路程．
（2）若高铁的平均速度(千米/时)是普通列车平均速度（千米/时)的倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短小时，求高铁的平均速度．
20．（6分）小明在证明“有两个角相等的三角形是等腰三角形”这一命题时，先画出图形，再写出“已知”，“求证”（如图），证明时他对所作的辅助线描述如下：“过点作的中垂线，垂足为”．
（1）请你判断小明辅助线的叙述是否正确；如果不正确，请改正．
（2）根据正确的辅助线的做法，写出证明过程．
21．（6分）化简求值：，其中x＝1．
22．（8分） “转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数；
(2)若对图(1)中星形截去一个角，如图(2)，请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；
(3)若再对图(2)中的角进一步截去，你能由题(2)中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程)
23．（8分）某广告公司为了招聘一名创意策划，准备从专业技能和创新能力两方面进行考核，成绩高者录取．甲、乙、丙三名应聘者的考核成绩以百分制统计如下：
（1）如果公司认为专业技能和创新能力同等重要，则应聘人 将被录取．
（2）如果公司认为职员的创新能力比专业技能重要，因此分别赋予它们6和4的权．计算他们赋权后各自的平均成绩，并说明谁将被录取．
24．（8分）定义：在平面直角坐标系中，对于任意两点，，若点满足，，那么称点是点，的融合点.
例如：，，当点满是，时，则点是点，的融合点，
（1）已知点，，，请说明其中一个点是另外两个点的融合点.
（2）如图，点，点是直线上任意一点，点是点，的融合点.
①试确定与的关系式.
②若直线交轴于点，当为直角三角形时，求点的坐标.
25．（10分）如图，在平面直角坐标系中，，，，点、在轴上且关于轴对称．

（1）求点的坐标；
（2）动点以每秒2个单位长度的速度从点出发沿轴正方向向终点运动，设运动时间为秒，点到直线的距离的长为，求与的关系式；
（3）在（2）的条件下，当点到的距离为时，连接，作的平分线分别交、于点、，求的长．
26．（10分）快车和慢车都从甲地驶向乙地，两车同时出发行在同一条公路上，途中快车休息1小时后加速行驶比慢车提前0.5小时到达目的地，慢车没有体息整个行驶过程中保持匀速不变．设慢车行驶的时间为x小时，快车行驶的路程为y1千米，慢车行驶的路程为y2千米，图中折线OAEC表示y1与x之间的函数关系，线段OD表示y2与x之间的函数关系，请解答下列问题：
（1）甲、乙两地相距 千米，快车休息前的速度是 千米/时、慢车的速度是 千米/时；
（2）求图中线段EC所表示的y1与x之间的函数表达式；
（3）线段OD与线段EC相交于点F，直接写出点F的坐标，并解释点F的实际意义．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、C
4、D
5、C
6、D
7、B
8、C
9、A
10、C
二、填空题(每小题3分,共24分)
11、x≥1
12、≠-1
13、k＜1．
14、1
15、6或
16、1
17、二、四.
18、①②③
三、解答题(共66分)
19、（1）普通列车的行驶路程是千米； （2）高铁的平均速度是千米/时
20、（1）不正确，应该是：过点作；（2）见解析
21、，.
22、（1）180°；（2）360°；（3）1080°．
23、（1）甲 （2）乙将被录取
24、（1）点是点，的融合点；（2）①，②符合题意的点为， .
25、（1）C（4，0）；（2）；（3）．
26、（1）300,75,60；（2）y1＝100x﹣150（3≤x≤4.5）；（3）点F的坐标为（3.75，225），点F代表的实际意义是在3.75小时时，快车与慢车行驶的路程相等