安徽省宿州埇桥区七校联考2023-2024学年八上数学期末质量检测试题含答案

这是一份安徽省宿州埇桥区七校联考2023-2024学年八上数学期末质量检测试题含答案，共8页。试卷主要包含了已知多项式，则b、c的值为等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题(每小题3分,共30分)
1．下列计算正确的是( )
A．B．
C．D．
2．两条直线与在同一直角坐标系中的图象位置可能为（ ）．
A．B．C．D．
3．对于实数、，定义一种新运算“”为：，这里等式右边是实数运算．例如：．则方程的解是（ ）
A．B．C．D．
4．若一个多边形的每个外角都等于60°，则它的内角和等于（ ）
A．180°B．720°C．1080°D．540°
5．ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定ABC为直角三角形的是（ ）
A．∠A+∠B=∠CB．∠A：∠B：∠C=1：2：3
C．a2=c2﹣b2D．a：b：c=3：4：6
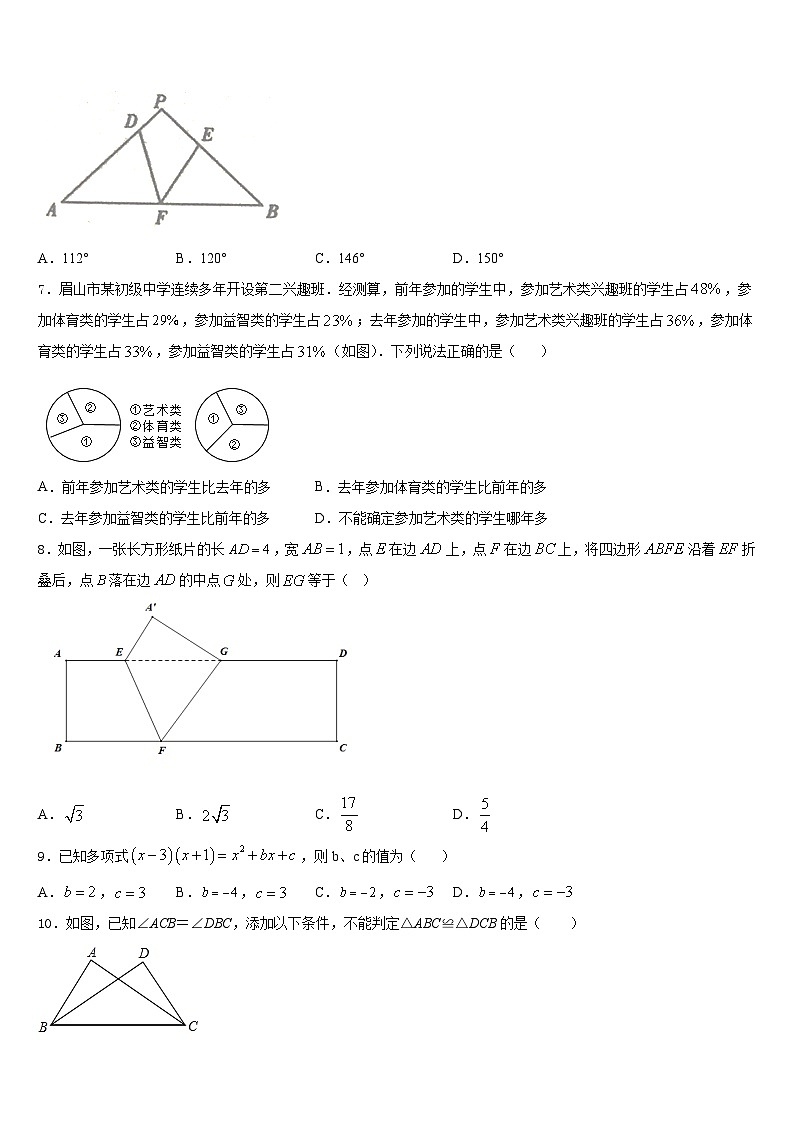
6．如图，在△PAB中，∠A=∠B，D、E、F分别是边PA、PB、AB上的点，且AD=BF，BE=AF．若∠DFE=34°，则∠P的度数为（ ）
A．112°B．120°C．146°D．150°
7．眉山市某初级中学连续多年开设第二兴趣班．经测算，前年参加的学生中，参加艺术类兴趣班的学生占，参加体育类的学生占，参加益智类的学生占；去年参加的学生中，参加艺术类兴趣班的学生占，参加体育类的学生占，参加益智类的学生占（如图）．下列说法正确的是（ ）
A．前年参加艺术类的学生比去年的多B．去年参加体育类的学生比前年的多
C．去年参加益智类的学生比前年的多D．不能确定参加艺术类的学生哪年多
8．如图，一张长方形纸片的长，宽，点在边上，点在边上，将四边形沿着折叠后，点落在边的中点处，则等于（ ）
A．B．C．D．
9．已知多项式，则b、c的值为（ ）
A．，B．，C．，D．，
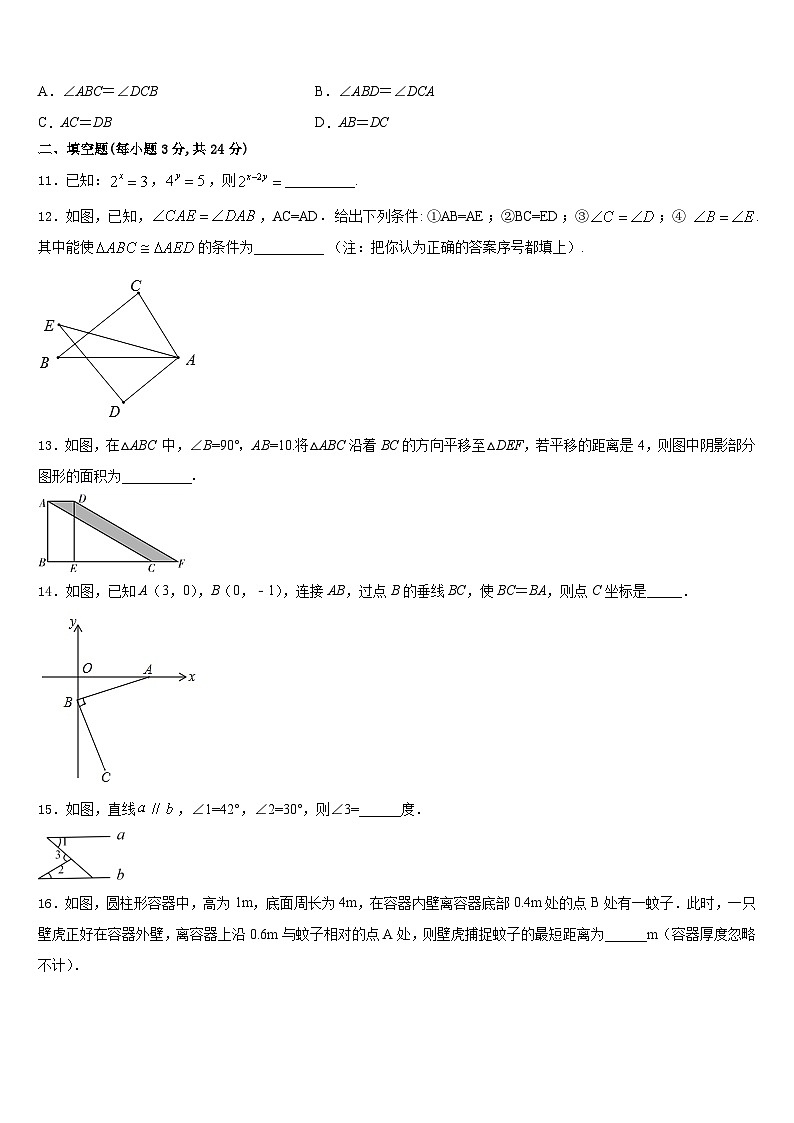
10．如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（ ）
A．∠ABC＝∠DCBB．∠ABD＝∠DCA
C．AC＝DBD．AB＝DC
二、填空题(每小题3分,共24分)
11．已知：，，则__________.
12．如图，已知，，AC=AD．给出下列条件: ①AB=AE；②BC=ED；③；④ .其中能使的条件为__________ （注：把你认为正确的答案序号都填上）.
13．如图，在△ABC 中，∠B=90°，AB=10.将△ABC沿着BC的方向平移至△DEF，若平移的距离是4，则图中阴影部分图形的面积为__________．
14．如图，已知A（3，0），B（0，﹣1），连接AB，过点B的垂线BC，使BC＝BA，则点C坐标是_____．
15．如图，直线，∠1=42°，∠2=30°，则∠3=______度．
16．如图，圆柱形容器中，高为1m，底面周长为4m，在容器内壁离容器底部0.4m处的点B处有一蚊子．此时，一只壁虎正好在容器外壁，离容器上沿0.6m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为______m（容器厚度忽略不计）．
17．若，则__________（填“”“”或“”）
18．如图，中，平分，平分，若，则__________
三、解答题(共66分)
19．（10分）（1）解方程．
（2）先化简 （）÷，再从x≤2的非负整数解中选一个适合的整数代入求值．
20．（6分）因式分解：a3﹣2a2b+ab2
21．（6分）如图，在中，，，点是上一动点，连结，过点作，并且始终保持，连结．
（1）求证：；
（2）若平分交于，探究线段之间的数量关系，并证明．
22．（8分）（基础模型）
已知等腰直角△ABC，∠ACB＝90°，AC＝CB，过点C任作一条直线l（不与CA、CB重合），过点A作AD⊥l于D，过点B作BE⊥l于 E．
（1）如图②，当点A、B在直线l异侧时，求证：△ACD≌△CBE
（模型应用）
在平面直角坐标性xOy中，已知直线l：y＝kx﹣4k（k为常数，k≠0）与x轴交于点A，与y轴的负半轴交于点 B．以AB为边、B为直角顶点作等腰直角△ABC．
（2）若直线l经过点（2，﹣3），当点C在第三象限时，点C的坐标为 ．
（3）若D是函数y＝x（x＜0）图象上的点，且BD∥x轴，当点C在第四象限时，连接CD交y轴于点E，则EB的长度为 ．
（4）设点C的坐标为（a，b），探索a，b之间满足的等量关系，直接写出结论．（不含字母k）
23．（8分）先化简，再求值并从中选取合适的整数代入求值．
24．（8分）受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如下表：
（1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？
（2）设从甲蔬菜棚调运蔬菜斤，总运费为元，试写出与的函数关系式，怎样安排调运方案才能使每天的总运费最省？
25．（10分）如图①，已知是等腰三角形，是边上的高，垂足为，是底边上的高，交于点．
（1）若．求证：≌；
（2）在图②, 图③中，是等腰直角三角形，点在线段上(不含点)，，且交于点，，垂足为．
ⅰ）如图②，当点与点重合，试写出与的数量关系；
ⅱ）如图③，当点在线段上(不含点，)时，ⅰ）中的结论成立吗？如果成立，请证明；如果不成立，请说明理由．
26．（10分）如图在等腰三角形△ABC中，AC=BC，D、E分别为AB、BC上一点，∠CDE=∠A．
（1）如图①，若BC=BD，求证：CD=DE；
（2）如图②，过点C作CH⊥DE，垂足为H，若CD=BD，EH=1，求DE﹣BE的值．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、B
5、D
6、A
7、D
8、D
9、C
10、D
二、填空题(每小题3分,共24分)
11、
12、①③④
13、1
14、C（1，﹣4）
15、1
16、
17、
18、120°
三、解答题(共66分)
19、 (1) 原分式方程无解．(1)1
20、
21、（1）见解析；（2），见解析
22、（1）详见解析；（2）(﹣6，﹣2)；（3）2；（1）a+ b=-1或b﹣a＝1．
23、，．
24、（1）甲、乙两蔬菜棚各调运了411斤、611斤蔬菜；（2）从甲蔬菜棚调运蔬菜811斤，从乙蔬菜棚调运蔬菜211斤总费用最省．
25、（1）见解析；（2）ⅰ）；ⅱ）成立，证明见解析
26、（1）证明见解析（1）1
到超市的路程（千米）
运费（元/斤·千米）
甲蔬菜棚
120
0.03
乙蔬菜棚
80
0.05