山东省微山县2023-2024学年数学八年级第一学期期末质量跟踪监视模拟试题含答案

这是一份山东省微山县2023-2024学年数学八年级第一学期期末质量跟踪监视模拟试题含答案，共6页。试卷主要包含了考生必须保证答题卡的整洁，下列说法中正确的个数是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．下列各式：，，，，其中分式共有几个（ ）．
A．1B．2C．3D．4
2．如图，在菱形ABCD中，对角线AC、BD相较于点O，BD＝8，BC＝5，AE⊥BC于点E，则AE的长为( )
A．5B．C．D．
3．若a+b=5，则代数式（﹣a）÷（）的值为（ ）
A．5B．﹣5C．﹣D．
4．点M（1，2）关于x轴对称的点的坐标为（ ）
A．（1，－2）B．（－1，2）C．（-1，－2）D．（2，－1）
5．若长方形的长为 (4a2-2a +1) ，宽为 (2a +1) ，则这个长方形的面积为（ ）
A．8a3-4a2+2a-1B．8a3-1
C．8a3+4a2-2a-1D．8a3 +1
6．已知一组数据20、30、40、50、50、50、60、70、80，其中平均数、中位数、众数的大小关系是（ ）
A．平均数＞中位数＞众数B．平均数＜中位数＜众数
C．中位数＜众数＜平均数D．平均数＝中位数＝众数
7．下列四个图案中，是轴对称图形的是（ ）
A．B．C．D．
8．下列说法中正确的个数是( )
①若是完全平方式，则k=3
②工程建筑中经常采用三角形的结构，这是利用三角形具有稳定性的性质
③在三角形内部到三边距离相等的点是三个内角平分线的交点
④当时
⑤若点P在∠AOB内部，D，E分别在∠AOB的两条边上，PD=PE,则点P在∠AOB的平分线上
A．1个B．2个C．3个D．4个
9．已知三角形三边长3，4，，则的取值范围是（ ）
A．B．C．D．
10．如图，在中，，点是边上的一点，点是的中点，若的垂直平分线经过点，，则（ ）
A．8B．6C．4D．2
二、填空题(每小题3分,共24分)
11．如图，点在等边的边上，，射线，垂足为点，点是射线上一动点，点是线段上一动点，当的值最小时，，则的长为___________________．
12．已知，，则的值是________________________．
13．若（x+m）（x+3）中不含x的一次项，则m的值为__．
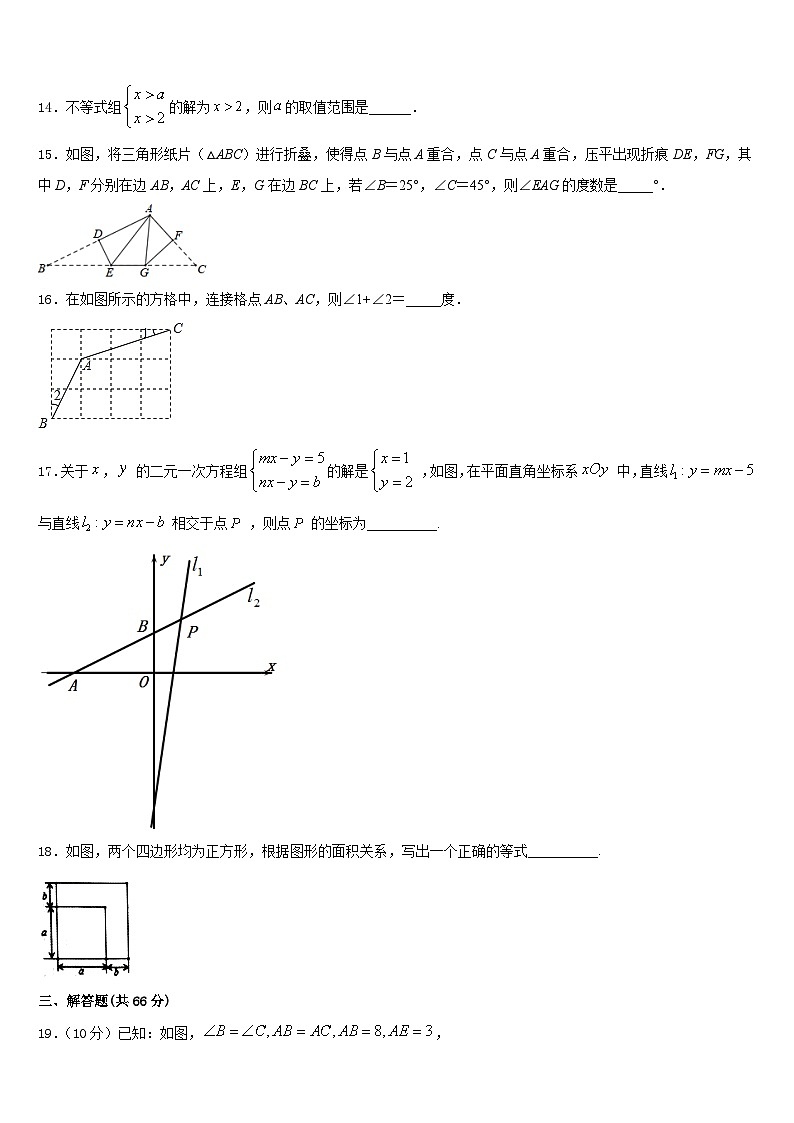
14．不等式组的解为，则的取值范围是______．
15．如图，将三角形纸片（△ABC）进行折叠，使得点B与点A重合，点C与点A重合，压平出现折痕DE，FG，其中D，F分别在边AB，AC上，E，G在边BC上，若∠B＝25°，∠C＝45°，则∠EAG的度数是_____°．
16．在如图所示的方格中，连接格点AB、AC，则∠1+∠2＝_____度．
17．关于， 的二元一次方程组的解是 ，如图，在平面直角坐标系 中，直线与直线 相交于点 ，则点 的坐标为__________.
18．如图，两个四边形均为正方形，根据图形的面积关系，写出一个正确的等式__________.
三、解答题(共66分)
19．（10分）已知：如图，，
(1)求证：.
(2)求的长.
20．（6分）亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位.
(1)计划调配36座新能源客车多少辆？该大学共有多少名志愿者？
(2)若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？
21．（6分）某玩具店用2000元购进一批玩具，面市后，供不应求，于是店主又购进同样的玩具，所购的数量是第一批数量的3倍，但每件进价贵了4元，结果购进第二批玩具共用了6300元.若两批玩具的售价都是每件120元，且两批玩具全部售完．
（1）第一次购进了多少件玩具？
（2）求该玩具店销售这两批玩具共盈利多少元？
22．（8分）某工厂要把一批产品从A地运往B地，若通过铁路运输，则每千米需交运费15元，还要交装卸费400元及手续费200元，若通过公路运输，则每千米需要交运费25元，还需交手续费100元（由于本厂职工装卸，不需交装卸费）.设A地到B地的路程为x km，通过铁路运输和通过公路运输需交总运费y1元和y2元，
（1）求y1和y2关于x的表达式.
（2）若A地到B地的路程为120km，哪种运输可以节省总运费？
23．（8分）某工厂要把一批产品从地运往地，若通过铁路运输，则每千米需交运费20元，还要交装卸费400元及手续费200元，若通过公路运输，则每千米需要交运费30元，还需交手续费100元（由于本厂职工装卸，不需交装卸费）．设地到地的路程为，通过铁路运输和通过公路运输需交总运费元和元．
（1）求和关于的函数表达式．
（2）若地到地的路程为，哪种运输可以节省总运费？
24．（8分）2019年11月26日，鲁南高铁日曲段正式开通，日照市民的出行更加便捷．从日照市到B市，高铁的行驶路线全程是600千米，普通列车的行驶路线全程是高铁的1.2倍．若高铁的平均速度是普通列车平均速度的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间节省4小时，求高铁的平均速度．
25．（10分）某商店销售篮球和足球共60个．篮球和足球的进价分别为每个40元和50元，篮球和足球的卖价分别为每个50元和65元．设商店共有x个足球，商店卖完这批球（篮球和足球）的利润为y．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）商店现将篮球每个涨价a元销售，足球售价不变，发现这批球卖完后的利润和x的取值无关．求卖完这批球的利润和a的值．
26．（10分）如图，，，.试说明：.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、B
4、A
5、D
6、D
7、D
8、C
9、C
10、C
二、填空题(每小题3分,共24分)
11、1
12、1
13、-1
14、
15、40°
16、1
17、
18、
三、解答题(共66分)
19、 (1)证明见详解；(2)BD=5.
20、 (1)计划36座的新能源客车6辆，共有218名志愿者；(2)调配36座新能源客车3辆，22座新能源客车5辆.
21、（1）第一次购进了25件玩具；（2）该玩具店销售这两批玩具共盈利3700元.
22、（1）；（2）铁路运输节省总运费.
23、（1），；（2）铁路运输节省总费用
24、高铁的平均速度是300千米/时．
25、（1）y＝5x＋600（0≤x≤60）；（2）a＝5，900元
26、见解析.