湖南省长沙市长沙天心区青雅丽发学校2023-2024学年八年级数学第一学期期末质量检测试题含答案

这是一份湖南省长沙市长沙天心区青雅丽发学校2023-2024学年八年级数学第一学期期末质量检测试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，已知，，，则、、的大小关系是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
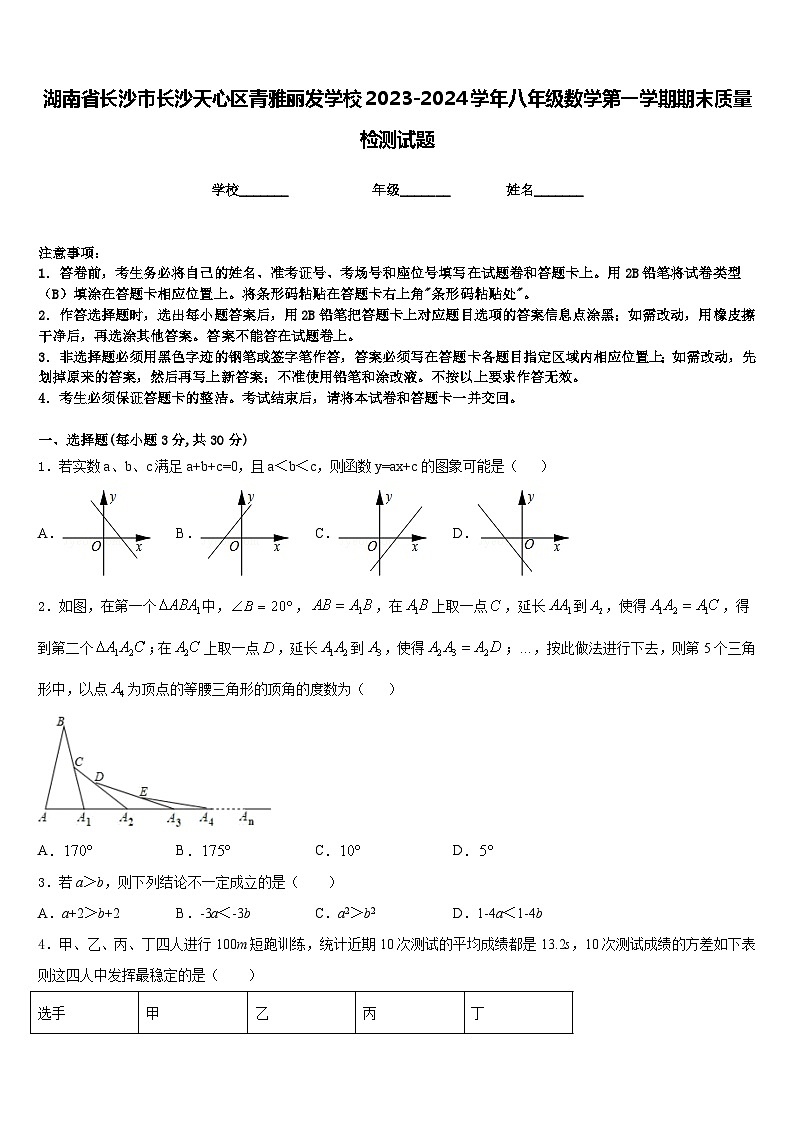
1．若实数a、b、c满足a+b+c=0，且a＜b＜c，则函数y=ax+c的图象可能是（ ）
A．B．C．D．
2．如图，在第一个中，，，在上取一点，延长到，使得，得到第二个；在上取一点，延长到，使得；…，按此做法进行下去，则第5个三角形中，以点为顶点的等腰三角形的顶角的度数为（ ）
A．B．C．D．
3．若a＞b，则下列结论不一定成立的是（ ）
A．a+2＞b+2B．-3a＜-3bC．a2＞b2D．1-4a＜1-4b
4．甲、乙、丙、丁四人进行100m短跑训练，统计近期10次测试的平均成绩都是13.2s，10次测试成绩的方差如下表则这四人中发挥最稳定的是（ ）
A．甲B．乙C．丙D．丁
5．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A．4B．3C．2D．1
6．某种秋冬流感病毒的直径约为0.000000203米，该直径用科学记数法表示为( )米．
A．2.03×10﹣8B．2.03×10﹣7C．2.03×10﹣6D．0.203×10﹣6
7．已知，，，则、、的大小关系是（ ）
A．B．C．D．
8．如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是（ ）
A．PC=PDB．∠CPD=∠DOPC．∠CPO=∠DPOD．OC=OD
9．一个正比例函数的图象过点(2，﹣3)，它的表达式为（ ）
A．B．C．D．
10．某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：
则该班学生一周读书时间的中位数和众数分别是（ ）
A．9，8B．9，9C．9.5，9D．9.5，8
二、填空题(每小题3分,共24分)
11．如图，，平分，为上一点，交于点，于， ，则_____.
12．使分式的值为0，这时x=_____．
13．计算：= ．
14．若|x+y+1|与（x﹣y﹣3）2互为相反数，则2x﹣y的算术平方根是_____．
15．一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为____________．
16．如图，在直角坐标系中有两条直线，l1：y＝x+1和L2：y＝ax+b，这两条直线交于轴上的点（0，1）那么方程组的解是_____．
17．已知多项式，那么我们把和称为的因式，小汪发现当或时，多项式的值为1．若有一个因式是（为正数），那么的值为______，另一个因式为______．
18．分解因式：x2﹣7x+12 =________．
三、解答题(共66分)
19．（10分）如图，△ABC和△DEF中，AB=DE，∠B=∠DEF．
（1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是 ；
（2）添加了条件后，证明△ABC≌△EFD．
20．（6分）为了比较+1与的大小，小伍和小陆两名同学对这个问题分别进行了研究.
（1）小伍同学利用计算器得到了，，所以确定+1 （填“＞”或“＜”或“=”）
（2）小陆同学受到前面学习在数轴上用点表示无理数的启发，构造出所示的图形，其中∠C=90°，BC=3，D在BC上且BD=AC=1.请你利用此图进行计算与推理，帮小陆同学对+1和的大小做出准确的判断.
21．（6分）如图，某中学校园内有一块长为米，宽为米的长方形地块．学校计划在中间留一块边长为米的正方形地块修建一座雕像，然后将阴影部分进行绿化．
（1）求绿化的面积．（用含的代数式表示）
（2）当时，求绿化的面积．
22．（8分）甲乙两人做某种机械零件，已知甲每小时比乙多做4个，甲做120个所用的时间与乙做100个所用的时间相等，求甲乙两人每小时各做几个零件？
23．（8分）如图，已知△ABC中，∠C=90°，∠B=15°，AC=2cm，分别以A、B两点为圆心，大于AB的长为半径画弧，两弧分别相交于E、F两点，直线EF交BC于点D，求BD的长．
24．（8分）如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点（端点除外），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ、CP交于点M，则在P、Q运动的过程中，
（1）求证：△ABQ ≌ △CAP；
（2）∠CMQ的大小变化吗？若变化，则说明理由，若不变，则求出它的度数；
（3）连接PQ,当点P、Q运动多少秒时，△APQ是等腰三角形？
25．（10分）如图，在四边形ABCD中，∠B=90°，AB∥ED ,交BC于E，交 AC于F， DE = BC,.
（1） 求证：△FCD 是等腰三角形
（2） 若AB=3.5cm,求CD的长．
26．（10分）如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为(2，4)
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）写出点A1的坐标；
（3）画出△A1B1C1向下平移3个单位长度所得的△A2B2C2；
（4）在x轴上找一点P，使PB+PC的和最小（标出点P即可，不用求点P的坐标）
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、C
4、B
5、B
6、B
7、D
8、B
9、A
10、A
二、填空题(每小题3分,共24分)
11、
12、1
13、1．
14、1
15、1
16、．
17、1
18、 (x-4)(x-3)
三、解答题(共66分)
19、（1）∠A=∠D (答案不唯一，也可以是∠ACB=∠DFE 或BE=CF 或 AC∥DF等等)；（2）见解析.
20、（1）> ；（2）见解析.
21、（1）平方米；（2）54平方米．
22、甲每小时做24个零件，乙每小时做1个零件．
23、4cm
24、（1）证明见解析；（2）∠CMQ的大小不变且为60度；（3）t=2.
25、（1）详见解析；（2）CD=1cm.
26、（1）见解析；（2）点A1的坐标为(-2,4)；（3）见解析；（4）见解析
选手
甲
乙
丙
丁
方差（s2）
0.020
0.019
0.021
0.022
读书时间（小时）
7
8
9
10
11
学生人数
6
10
9
8
7