陕西省西安市西安交通大附属中学2023-2024学年数学八年级第一学期期末学业水平测试试题含答案

这是一份陕西省西安市西安交通大附属中学2023-2024学年数学八年级第一学期期末学业水平测试试题含答案，共8页。试卷主要包含了答题时请按要求用笔，如图，直线，则，下列函数中，随值增大而增大的是，分式可变形为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．已知函数的图象如左侧图象所示，则的图象可能是( )
A．B．
C．D．
2． “2019武汉军运会”部分体育项目的示意图中是轴对称图形的是（ ）
A．B．C．D．
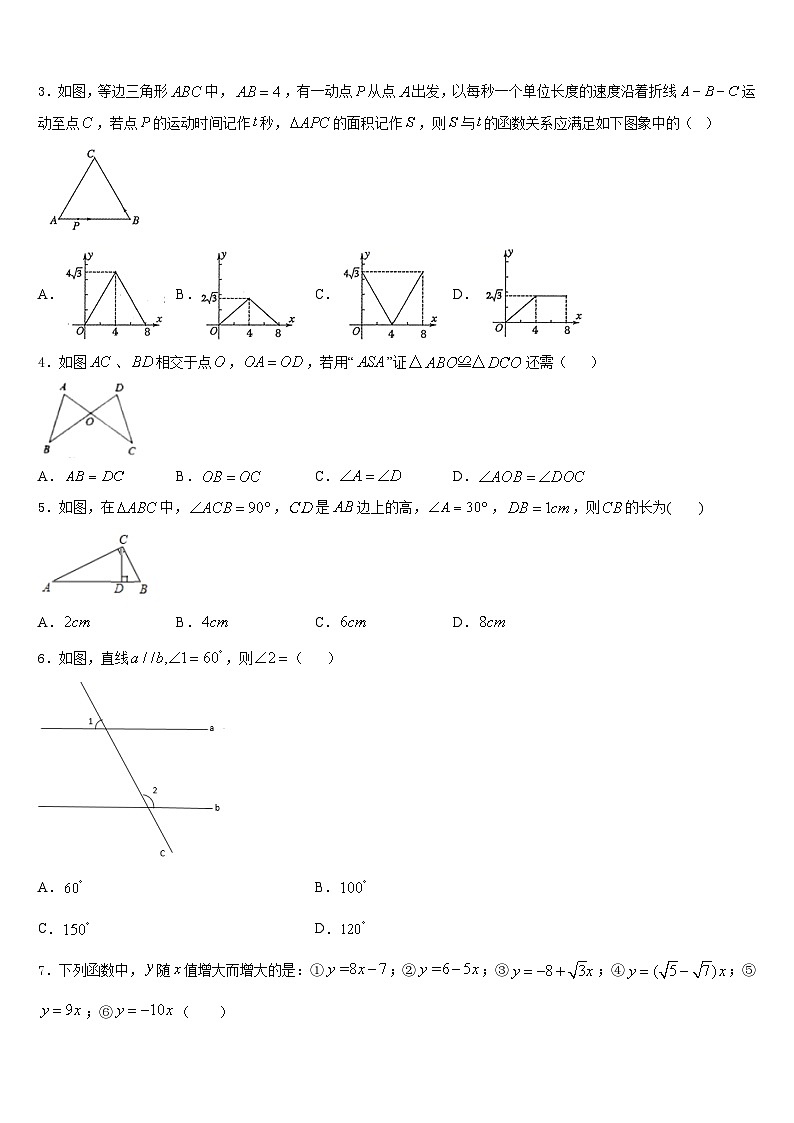
3．如图，等边三角形中，，有一动点从点出发，以每秒一个单位长度的速度沿着折线运动至点，若点的运动时间记作秒，的面积记作，则与的函数关系应满足如下图象中的（ ）
A．B．C．D．
4．如图、相交于点，，若用“”证还需（ ）
A．B．C．D．
5．如图，在中，，是边上的高，，，则的长为( )
A．B．C．D．
6．如图，直线，则（ ）
A．B．
C．D．
7．下列函数中，随值增大而增大的是：①；②；③；④；⑤；⑥（ ）
A．①②③B．③④⑤C．②④⑤D．①③⑤
8．下列四组数据，能作为直角三角形的三边长的是（ ）
A．2、4、6B．2、3、4C．5、7、12D．8、15、17
9．分式可变形为（ ）
A．B．C．D．
10．如图，，AE与BD交于点C，，则的度数为（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．当________时，二次根式有意义.
12．若式子在实数范围内有意义，则的取值范围是__________．
13．已知一个多边形的内角和是外角和的，则这个多边形的边数是 .
14．已知，则___________.
15．若等腰三角形的一边，一边等于，则它的周长等于_____________．
16．若点P关于x轴的对称点为P1（2a+b, －a+1），关于y轴对称点的点为
P2（4－b,b+2），则点P的坐标为
17．已知，分别是的整数部分和小数部分，则的值为_______．
18．在坐标系中，已知点关于轴，轴的对称点分别为，，若坐标轴上的点恰使，均为等腰三角形，则满足条件的点有______个．
三、解答题(共66分)
19．（10分）如图1，已知矩形ABCD，连接AC，将△ABC沿AC所在直线翻折，得到△AEC，AE交CD于点F．
（1）求证：DF=EF；
（2）如图2，若∠BAC=30°，点G是AC的中点，连接DE，EG，求证：四边形ADEG是菱形．
20．（6分）问题探究：小明根据学习函数的经验，对函数的图象与性质进行了探究．
下面是小明的探究过程，请你解决相关问题：
在函数中，自变量x可以是任意实数；
如表y与x的几组对应值：
______；
若，为该函数图象上不同的两点，则______；
如图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象：
该函数有______填“最大值”或“最小值”；并写出这个值为______；
求出函数图象与坐标轴在第二象限内所围成的图形的面积；
观察函数的图象，写出该图象的两条性质．
21．（6分）为响应珠海环保城市建设，我市某污水处理公司不断改进污水处理设备，新设备每小时处理污水量是原系统的1.5倍，原来处理1200m3污水所用的时间比现在多用10小时．
（1）原来每小时处理污水量是多少m2？
（2）若用新设备处理污水960m3，需要多长时间？
22．（8分）如图1，在△ABC和△ADE中，∠BAC＝∠EAD，AB＝AC，AD＝AE，连接CD、AE交于点F．
（1）求证：BE＝CD．
（2）当∠BAC＝∠EAD＝30°，AD⊥AB时（如图2），延长DC、AB交于点G，请直接写出图中除△ABC、△ADE以外的等腰三角形．
23．（8分）四边形ABCD中，AD=CD，AB=CB，我们把这种两组邻边分别相等的四边形叫做“筝形”．“筝形”是一种特殊的四边形，它除了具有两组邻边分别相等的性质外，猜想它还有哪些性质？然后证明你的猜想．（以所给图形为例，至少写出三种猜想结果，用文字和字母表示均可，并选择猜想中的其中一个结论进行证明）
24．（8分）如图，已知Rt△ABC≌Rt△ADE，∠ABC＝∠ADE＝90°，BC与DE相交于点F，连结CD、BE．
（1）请你找出图中其他的全等三角形；
（2）试证明CF＝EF．
25．（10分）育红中学在元旦举行了一次成语知识竞赛，满分为分，学生得分均为整数，成绩达到分及分以上为合格，达到分或分为优秀．这次竞赛中甲、乙两组学生成绩分布的折线图如图所示：
（1）求出成绩统计分析表中，的值；
（2）张明说：“这次竞赛我得了分，在我们小组中排名属于中游略偏上！”观察上面的表格和折线图，判断张明是甲、乙哪个组的学生，简单说明理由．
（3）乙组同学说他们组的合格率、优秀率均高于甲组，所以他们组的成绩好于甲组，但是甲组同学不同意乙组同学的说法，认为他们组的成绩要好于乙组．请你写出两条支持甲组同学观点的理由．
26．（10分）在利用构造全等三角形来解决的问题中，有一种典型的利用倍延中线的方法，例如：在△ABC中，AB＝8，AC＝6，点D是BC边上的中点，怎样求AD的取值范围呢？我们可以延长AD到点E，使AD＝DE，然后连接BE（如图①），这样，在△ADC和△EDB中，由于，∴△ADC≌△EDB，∴AC＝EB，接下来，在△ABE中通过AE的长可求出AD的取值范围．
请你回答：
（1）在图①中，中线AD的取值范围是 ．
（2）应用上述方法，解决下面问题
①如图②，在△ABC中，点D是BC边上的中点，点E是AB边上的一点，作DF⊥DE交AC边于点F，连接EF，若BE＝4，CF＝2，请直接写出EF的取值范围．
②如图③，在四边形ABCD中，∠BCD＝150°，∠ADC＝30°，点E是AB中点，点F在DC上，且满足BC＝CF，DF＝AD，连接CE、ED，请判断CE与ED的位置关系，并证明你的结论．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、A
4、C
5、A
6、D
7、D
8、D
9、D
10、D
二、填空题(每小题3分,共24分)
11、≤3
12、a＞﹣1
13、2
14、2
15、16或1
16、（2a+b,b+2）
17、
18、5
三、解答题(共66分)
19、（1）证明见详解；（2）证明见详解．
20、 (2)0；；(3)①最大值，3；②；③函数图象为轴对称图形，对称轴为y轴；当时，y随x的增大而增大，当时，y随x增大而减小.
21、（1）原来每小时处理污水量是40m2；（2）需要16小时．
22、（1）见解析；（2）△ACF是等腰三角形，△ADG是等腰三角形，△DEF是等腰三角形，△ECD是等腰三角形．
23、①筝形具有轴对称性；或△ABD与△CBD关于直线BD对称；②筝形有一组对角相等；或∠DAB=∠DCB；③筝形的对角线互相垂直；或AC⊥BD；④筝形的一条对角线平分另一条对角线；或BD平分AC；⑤筝形的一条对角线平分一组对角；或BD平分∠ADC和∠ABC；详见解析
24、（1）图中其它的全等三角形为：①△ACD≌△AEB，②△DCF≌△BEF；（2）证明过程见解析；
25、（1）分，；（2）他是乙组的学生；（3）①甲组的平均分高于乙组，即甲组的总体平均水平高；②甲组的方差比乙组小，即甲组的成绩比乙组稳定.
26、（1）1＜AD＜7；（2）①2＜EF＜6；②CE⊥ED，理由见解析
x
0
1
2
3
4
y
0
1
2
3
2
1
a
组别
平均数
中位数
方差
合格率
优秀率
甲组
乙组