山东省德州市武城县2021-2022学年八年级上学期期末考试数学试题

这是一份山东省德州市武城县2021-2022学年八年级上学期期末考试数学试题，共24页。试卷主要包含了单选题，填空题，解答题，计算题，作图题，证明题等内容，欢迎下载使用。

一、单选题
1．第十四届全运会中，山东代表团以58枚金牌、55枚银牌、47枚铜牌，总计160枚奖牌的成绩锁定奖牌榜第一的位置，下列关于体育的图形中是轴对称图形的是（ ）
A．B．C．D．
2．下列长度的三段钢条，不能组成一个三角形框架的是 （ ）
A．，，B．，，
C．，，D．，，
3．下列计算中正确的是（ ）
A．B．C．D．
4．一个正多边形的一个外角是，则该正多边形的内角和是（ ）
A．B．C．D．
5．如果把分式中的x和y都扩大2倍，那么分式的值（ ）
A．不变B．扩大2倍C．扩大4倍D．缩小2倍
6．如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪一块去（ ）
A．B．C．D．和
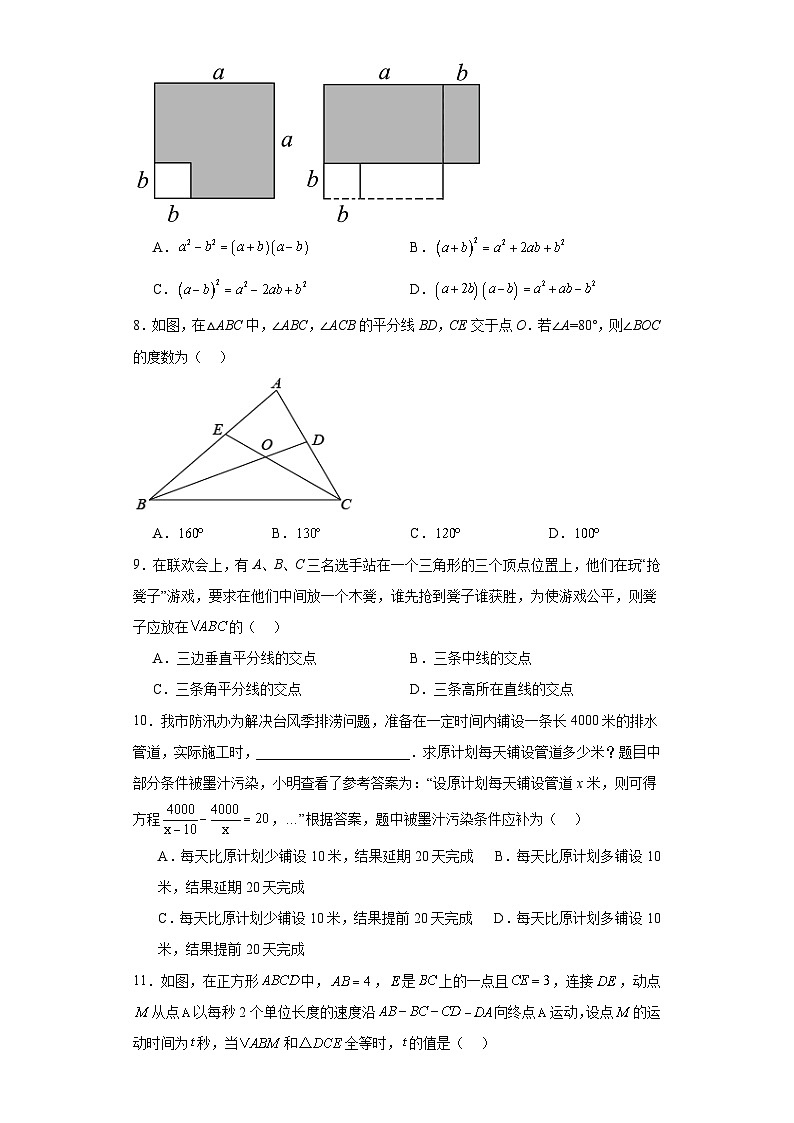
7．如图，边长为a的正方形中挖掉边长为b的正方形（a＞b），把剩下的部分拼成一个矩形，通过计算两处图形的面积，验证了一个等式，此等式是（ ）
A．B．
C．D．
8．如图，在△ABC中，∠ABC，∠ACB的平分线BD，CE交于点O．若∠A=80°，则∠BOC的度数为（ ）
A．B．C．D．
9．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放在的（ ）
A．三边垂直平分线的交点B．三条中线的交点
C．三条角平分线的交点D．三条高所在直线的交点
10．我市防汛办为解决台风季排涝问题，准备在一定时间内铺设一条长4000米的排水管道，实际施工时，______________________．求原计划每天铺设管道多少米？题目中部分条件被墨汁污染，小明查看了参考答案为：“设原计划每天铺设管道x米，则可得方程，…”根据答案，题中被墨汁污染条件应补为（ ）
A．每天比原计划少铺设10米，结果延期20天完成B．每天比原计划多铺设10米，结果延期20天完成
C．每天比原计划少铺设10米，结果提前20天完成D．每天比原计划多铺设10米，结果提前20天完成
11．如图，在正方形中，，是上的一点且，连接，动点从点以每秒2个单位长度的速度沿向终点运动，设点的运动时间为秒，当和全等时，的值是（ ）
A．3.5B．5.5C．6.5D．3.5或6.5
12．明明和乐乐下棋，明明执圆形棋子，乐乐执方形棋子，如图，棋盘中心的方子的位置用表示，右下角方子的位置用表示，明明将第4枚圆形棋子放入棋盘后，所有的棋子构成轴对称图形，则明明放的位置可能是（ ）
A．B．C．D．
二、填空题
13．芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食品和药物，得到广泛的使用。经测算，一粒芝麻的质量约为0.00000201千克，将0.00000201用科学记数法表示为 ．
14．已知，，则 ．
15．如图所示，在中，，，EF垂直平分BC，交AC于点D，交BC于点G，点P为直线EF上一动点，则周长的最小值是 ．
16．在平面直角坐标系中，若点A（1+m，1-n）与点B（-3，2）关于y轴对称，则 ．
17．如图所示，折叠直角三角形纸片的直角，使点落在上的点处，已知，，则的长是 ．
18．如图，中，、的角平分线、交于点P，延长、，则下列结论中正确的有 ．（将所有正确序号填在横线上）
①平分；②，③；④若，，则．
三、解答题
19．（1）解方程
（2）解方程
（3）分解因式
四、计算题
20．先化简，，然后从，0，1，3中选一个你认为合适的数作为x值，代入求值．
五、作图题
21．在平面直角坐标系中的位置如图所示、、三点在格点上．
（1）作出关于轴对称的，并写出点的坐标；
（2）作出关于对称的，并写出点的坐标；
（3）求的面积．
22．已知：如图，在中，，边的垂直平分线与分别交于点D和点E．
（1）作出边的垂直平分线（尺规作图，保留作图痕迹）；
（2）当时，求的度数．
六、证明题
23．两个大小不同的等腰直角三角板如图所示放置，右图是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．
（1）求证：△ABE≌△ACD；
（2）若图2中的BE＝3CE，CD＝6，求 △DCE的面积．
七、解答题
24．“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办，小张去离家2520米的奥体中心看演唱会，到奥体中心后，发现演唱会门票忘带了，此时离演唱会开始还有23分钟，于是他跑步回家，拿到票后立刻找到一辆“共享单车”原路赶回奥体中心，已知小张骑车的时间比跑步的时间少用了4分钟，且骑车的平均速度是跑步的平均速度的1.5倍．
（1）求小张跑步的平均速度；
（2）如果小张在家取票和寻找“共享单车”共用了5分钟，他能否在演唱会开始前赶到奥体中心？说明理由．
25．如图所示，已知中，∠B=90°，AB=16cm，AC=20cm．P、Q是的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒lcm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．
（1）BC= cm；
（2）求当点P在边AC的垂直平分线上时CQ的值；
（3）当点Q在边CA上运动时，直接写出使为等腰三角形的运动时间．
参考答案：
1．C
【分析】根据轴对称图形的概念对各选项分析判断即可得解．
【详解】选项A、B、D均不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项C能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：C．
【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．C
【分析】根据构成三角形的条件，三角形的三边关系逐项判断即可，两边之和大于第三边，两边之差小于第三边．
【详解】A.，能组成一个三角形框架，故该选项不符合题意；
B.，能组成一个三角形框架，故该选项不符合题意；
C.，不能组成一个三角形框架，故该选项符合题意；
D.，能组成一个三角形框架，故该选项不符合题意；
故选C
【点睛】本题考查了构成三角形的条件，掌握三角形的三边关系是解题的关键．
3．D
【分析】根据幂的运算法则即可依次判断．
【详解】解：A、，不是同类项无法计算，故选项错误，不符合题意；
B、，故选项错误，不符合题意；
C、，故选项错误，不符合题意；
D、，故选项正确，符合题意．
故选：D．
【点睛】本题主要考查幂的运算，解题的关键是熟知幂的运算法则．
4．A
【分析】根据多边形的边数与多边形的外角的个数相等，可求出该正多边形的边数，再由多边形的内角和公式求出其内角和．
【详解】解：该正多边形的边数为：360°÷60°=6，
该正多边形的内角和为：（6-2）×180°=720°．
故选：A．
【点睛】本题考查了多边形的内角与外角，熟练掌握多边形的外角和与内角和公式是解答本题的关键．
5．B
【分析】依题意，分别用2x和2y去代换原分式中的x和y，利用分式的基本性质化简即可．
【详解】解：分别用2x和2y去代换原分式中的x和y，
得，
可见新分式扩大为原来的2倍．
故选：B．
【点睛】本题主要考查了分式的基本性质，解题的关键是抓住分子、分母变化的倍数．要注意：解此类题首先把字母变化后的值代入式子中，然后约分，再与原式比较，最终得出结论．
6．C
【分析】观察每块玻璃形状特征，利用ASA判定三角形全等即可得出答案．
【详解】解：第块和第块只保留了原三角形的一个角和部分边，根据这两块中的任一快均不能配一块与原来完全一样的，第块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃，应带去，
故选：C．
【点睛】本题属于利用ASA判定三角形全等的实际应用，难度不大，要善于将所学知识与实际问题相结合，解题的关键是熟练掌握全等三家形的判定定理．
7．A
【分析】由图可知，正方形剩下的面积为：，矩形宽为；长为；得面积：，根据两者面积相等，即可求出答案．
【详解】由图得，正方形剩下面积：
∵矩形边长为，
∴矩形面积：
又∵正方形面积等于矩形面积
∴
故选：A．
【点睛】本题考查整式乘法，平方差公式；解题的关键是掌握几何图形与整式乘法的运用．
8．B
【分析】在△ABC中，利用三角形内角和定理可求出（∠ABC+∠ACB）的度数，由角平分线的定义可求出（∠OBC+∠OCB）的度数，再在△BCO中，利用三角形内角和定理可求出∠BOC度数．
【详解】解：在△ABC中，∠ABC+∠ACB=180°-∠A=100°．
∵BO平分∠ABC，CO平分∠ACB，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=50°．
在△BCO中，∠BOC=180°-（∠OBC+∠OCB）=130°．
故选：B．
【点睛】本题考查了三角形内角和定理以及角平分线的定义，利用三角形内角和定理及角平分线的定义，找出（∠OBC+∠OCB）的度数是解题的关键．
9．A
【分析】根据题意可知，当木凳所在位置到A、B、C三个顶点的距离相等时，游戏公平，再由线段垂直平分线的性质即可求解．
【详解】解：由题意可得：当木凳所在位置到A、B、C三个顶点的距离相等时，游戏公平，
∵线段垂直平分线上的点到线段两端的距离相等，
∴木凳应放的最适当的位置是在的三边垂直平分线的交点，
故选：A．
【点睛】本题考查线段垂直平分线的性质的应用，掌握线段垂直平分线的性质是解题的关键．
10．A
【分析】工作时间=工作总量÷工作效率．那么4000÷x表示原来的工作时间，那么4000÷（x-10）就表示现在的工作时间，20就代表原计划比现在多的时间．
【详解】解：原计划每天铺设管道x米，那么（x-10）就应该是实际每天比原计划少铺了10米，
而用，则实际用的时间-表示用原计划的时间=20天，
那么就说明每天比原计划少铺设10米，结果延期20天完成．
故选：A．
【点睛】本题考查了由实际问题抽象除法分式方程，是根据方程来判断缺失的条件，要注意方程所表示的意思，结合题目给出的条件得出正确的判断．
11．D
【分析】根据点M的位置分类讨论，分别画出对应的图形，根据全等三角形的性质和时间=路程÷速度分别求解即可．
【详解】解：当点M在AB上时，显然A、B、M构不成三角形，故不符合题意；
当点M运动到BC上时，连接AM，如下图所示
∵四边形ABCD为正方形
∴AB=DC=4，∠B=∠C=90°，结合题意，可知≌
∴BM=CE=3
∴点M运动的路程为AB＋BM=7
∴此时t=7÷2=；
当点M运动到CD上时，连接AM、BM，如下图所示
∵四边形ABCD为正方形
∴AB=DC=4，
由图易知AM和BM均大于CE，
∴此时不存在和全等；
当点M运动到DA上时，连接BM，如下图所示
∵四边形ABCD为正方形
∴AD=BC=AB=CD=4，∠A=∠C=90°，结合题意，可知≌
∴AM=CE=3
∴点M运动的路程为AB＋BC＋CD＋AD－AM=13
∴此时t=13÷2=；
综上：t的值为或
故选D．
【点睛】此题考查的是全等三角形与动点问题，掌握全等三角形的性质和分类讨论的数学思想是解题关键．
12．D
【分析】根据题意建立平面直角坐标系，再根据轴对称图形的定义确定第4枚方形的位置，即可解答．
【详解】如图所示，符合题意点的坐标是（−1，1），故D正确．
故选：D．
【点睛】本题主要考查了轴对称图形的性质以及点的坐标，正确得出原点位置是解题关键．
13．
【分析】根据科学记数法的表示计算即可；
【详解】；
故答案为：．
【点睛】本地主要考查了科学记数法的表示，准确计算是解题的关键．
14．72
【分析】先逆用同底数幂的乘法，将原式变形为，再逆用幂的乘方，变形为，最后把已知代入计算即可．
【详解】解：
，
故答案为：72．
【点睛】本题考查同底数幂的乘法和幂的乘方，逆用同底数幂的乘法和幂的乘方法则将式子恒等变形是解题的关键．
15．7
【分析】根据题意知BP=PC，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可得到结论．
【详解】解：如图所示连接PC，
∵垂直平分，
∴BP=PC，
∴AP+BP=AP+PC，
∵△ABP的周长=AB+BP+AP，
∴要使△ABP的周长最小，即AP+BP最小，
∴要想使得AP+BP的值最小，则AP+PC的值最小，
∴当A、P、C三点共线时，
设交于点D，
∴当P和D重合时，的值最小，最小值等于的长，
∴周长的最小值是．
故答案为：7．
【点睛】本题考查了线段垂直平分线的性质，轴对称-最短路线问题的应用，解题的关键是找出P的位置．
16．1
【分析】关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变．直接利用关于y轴对称点的性质得出m，n的值，进而得出答案．
【详解】解：∵点A（1+m，1-n）与点B（-3，2）关于y轴对称，
∴1+m=3，1-n=2，
解得：m=2，n=-1，
∴m+n=2-1=1．
故答案为：1．
【点睛】本题主要考查了关于y轴对称点的特征，点P（x，y）关于y轴的对称点P′的坐标是（-x，y）．
17．12
【分析】设OC=x，则OB=BC－OC=18－x，由折叠的性质可知：OD=OC=x，∠ADO=∠C=90°，然后利用30°所对的直角边是斜边的一半即可列出方程，求出x，从而得出结论．
【详解】解：设OC=x，则OB=BC－OC=18－x
由折叠的性质可知：OD=OC=x，∠ADO=∠C=90°
∴∠BDO=180°－∠ADO=90°
在Rt△BDO中，∠B=30°
∴OB=2OD=2x，
∴18－x=2x
解得：x=6
∴OB=2×6=12
故答案为：12．
【点睛】此题考查的是折叠的性质和直角三角形的性质，掌握折叠的性质和30°所对的直角边是斜边的一半是解题关键．
18．①②③④
【分析】①作PD⊥AC于D．由角平分线的性质得出PM=PN，PM=PD，得出PM=PN=PD，即可得出①正确；②首先证出∠ABC+∠MPN=180°，证明Rt△PAM≌Rt△PAD（HL），得出∠APM=∠APD，同理：Rt△PCD≌Rt△PCN（HL），得出∠CPD=∠CPN，即可得出②正确；③由角平分线和三角形的外角性质得出∠CAE=∠ABC+∠ACB，∠PAM=∠ABC+∠APB，得出∠ACB=2∠APB，③正确；④由全等三角形的性质得出AD=AM，CD=CN，即可得出④正确；即可得出答案．
【详解】解：①作PD⊥AC于D．
∵PB平分∠ABC，PA平分∠EAC，PM⊥BE，PN⊥BF，
∴PM=PN，PM=PD，
∴PM=PN=PD，
∴点P在∠ACF的角平分线上，故①正确；
②∵PM⊥AB，PN⊥BC，
∴∠ABC+90°+∠MPN+90°=360°，
∴∠ABC+∠MPN=180°，
在Rt△PAM和Rt△PAD中，
，
∴Rt△PAM≌Rt△PAD（HL），
∴∠APM=∠APD，
同理：Rt△PCD≌Rt△PCN（HL），
∴∠CPD=∠CPN，
∴∠MPN=2∠APC，
∴∠ABC+2∠APC=180°，②正确；
③∵PA平分∠CAE，BP平分∠ABC，
∴∠CAE=2∠PAM，
∵∠CAE=∠ABC+∠ACB，∠PAM=∠ABC+∠APB，
∴∠ACB=2∠APB，③正确；
④∵Rt△PAM≌Rt△PAD（已证），
∴AD=AM，
∵Rt△PCD≌Rt△PCN（已证），
∴CD=CN，
∴AM+CN=AD+CD=AC，④正确；
故答案为：①②③④．
【点睛】本题考查了角平分线的性质定理和判定定理，全等三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和，有一定综合性，但难度不大，只要仔细分析便不难求解．
19．(1)原方程无解．(2)．(3)．
【分析】(1)通过去分母、去括号、移项、合并同类项、系数化为1，检验，即可求解．
(2)通过去分母、去括号、移项、合并同类项、系数化为1，检验，即可求解．
(3)通过提公因式，套用完全平方公式即可求解．
【详解】(1)原方程化为： ，
去分母得：
去括号、移项、合并同类项得： ，
解得：
检验：当时， ，
∴ 是原方程的增根．
∴原方程无解．
(2) 原方程化为：
去分母得：
去括号得：
移项、合并同类项得：
解得：
检验：当时，
∴是原方程的解．
(3)原式=
=
=．
【点睛】本题考查解分式方程，因式分解，解题的关键是熟悉解分式方程的步骤，特别是在去分母时找准最简公分母，因式分解的关键在于对提公因式法，完全平方公式的熟练运用．
20．，
【分析】原式括号中两项通分并利用同分母分式的减法法则变形，再利用除法法则变形，约分得到最简结果，把x=3代入计算即可求出值．
【详解】：原式=
，
∵
∴当x=3时，原式=．
【点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．注意取值时需要考虑分式的分母不为0．
21．（1）见解析；点的坐标；（2）见解析；点的坐标；（3）．
【分析】（1）根据画轴对称图形的方法进行作图即可得，再根据用坐标表示轴对称即可得点的坐标；
（2）根据画轴对称图形的方法进行作图即可得，再根据用坐标表示轴对称即可得点的坐标；
（3）连接，可知三角形是以，直角边的直角三角形，根据三角形的面积公式进行解答即可得．
【详解】（1）如图，过点B画y轴的垂线，垂足为D，在垂线上截取，就是点B关于y轴的对称点；同理，分别画出点A，C关于y轴的对称点，；连接，，，则即为所求，点的坐标；
∵点关于y轴对称的点的坐标为，
∴点的坐标；
（2）如图，过点B画x轴的垂线，垂足为E，在垂线上截取，就是点B关于x轴的对称点；同理，分别画出点A，C关于x轴的对称点，；连接，，，则即为所求，
∵点关于x轴对称的点的坐标为，
∴点的坐标；
（3）如图，连接，
由图可知，三角形是以，直角边的直角三角形，
∴．
【点睛】本题考查了作图—轴对称变换，解题的关键是熟记作图方法：几何图形都可以看作由点组成，我们只要分别作出这些点关于对称轴的对应点，再连接这些对应点，就可以得到原图形的轴对称图形．
22．（1）如图所示，见解析；（2）．
【分析】（1）利用线段垂直平分线的作法得出即可；
（2）连接CE，利用垂直平分线的性质证明出，再通过计算∠ACB的角度得出∠A的度数．
【详解】（1）如图所示，即为所求作的边的垂直平分线；
（2）如图，连接，
∵是的垂直平分线，
∴，
∴，
∵，
∴，
∴，
设，
则，
在中，，
∴，
解得，
即．
【点睛】本题考查了垂直平分线的作法和性质，等腰三角形等边对等角，以及三角形内角之间的关系，熟练掌握这些知识是解题的关键．
23．（1）见解析；（2）6
【分析】（1）由等腰直角三角形的性质可知，，根据图形即可证明∠BAE=∠CAD，最后即可利用“SAS”判定．
（2）由，得出．由等腰直角三角形的性质可知，即可证明，结合题意，即可求出CE的长，最后利用三角形面积公式求面积即可．
【详解】（1）证明：∵和均为等腰直角三角形，
∴，，
∴∠BAC+∠CAE= ∠EAD+∠CAE，
∴∠BAE=∠CAD．
在和中，，
∴．
（2）由（1）中知：．
∵和均为等腰直角三角形，
∴，
∴，
∴，
又∵，即，
∴CE=2，
∴．
【点睛】本题考查等腰直角三角形的性质，三角形全等的判定和性质．掌握三角形全等的判定和性质是解答本题的关键．
24．（1）小张跑步的平均速度为210米/分钟．（2）小张不能在演唱会开始前赶到奥体中心．
【详解】试题分析：（1）设小张跑步的平均速度为x米/分钟，则小张骑车的平均速度为1.5x米/分钟，根据时间=路程÷速度结合小张骑车的时间比跑步的时间少用了4分钟，即可得出关于x的分式方程，解之并检验后即可得出结论；
（2）根据时间=路程÷速度求出小张跑步回家的时间，由骑车与跑步所需时间之间的关系可得出骑车的时间，再加上取票和寻找“共享单车”共用的5分钟即可求出小张赶回奥体中心所需时间，将其与23进行比较后即可得出结论．
试题解析：（1）设小张跑步的平均速度为x米/分钟，则小张骑车的平均速度为1.5x米/分钟，
根据题意得： =4，解得：x=210，
经检验，x=210是原方程组的解，
答：小张跑步的平均速度为210米/分钟；
（2）小张跑步到家所需时间为2520÷210=12（分钟），
小张骑车所用时间为12﹣4=8（分钟），
小张从开始跑步回家到赶回奥体中心所需时间为12+8+5=25（分钟），
∵25＞23，
∴小张不能在演唱会开始前赶到奥体中心．
25．（1）12；（2）13cm；（3）当t为11秒或12秒或13.2秒时，△BCQ为等腰三角形．
【分析】（1）由勾股定理可得：，从而可得答案；
（2）画出符合题意的图形，利用垂直平分线的性质得到：， 再利用勾股定理求解时间， 从而可得答案；
（3）分三种情况讨论，当 证明， 可得此时的时间，当， 结合已知条件求解时间即可，当时，过B点作BE⊥AC于点E，利用等面积法求解， 再利用勾股定理求解，利用等腰三角形的三线合一可得的长度，从而可得此时的时间， 从而可解答此问.
【详解】解：（1）∵∠B=90°，AB=16cm，AC=20cm
∴BC===12（cm）．
故答案为：12；
（2）如图，
∵点P在边AC的垂直平分线上，
∴PC=PA=t，PB=16-t，
在中，，
即
解得：t=．
此时，点Q在边AC上，CQ=2×−12＝13（cm）；
（3）①当CQ=BQ时，如图1所示，
则∠C=∠CBQ，
∵∠ABC=90°，
∴∠CBQ+∠ABQ=90°．∠A+∠C=90°，
∴∠A=∠ABQ，
∴BQ=AQ，
∴CQ=AQ=10，
∴BC+CQ=22，
∴t=22÷2=11秒．
②当CQ=BC时，如图2所示，
则BC+CQ=24，
∴t=24÷2=12秒．
③当BC=BQ时，如图3所示，
过B点作BE⊥AC于点E，
由
∴BE＝＝＝，
∴CE＝=．
∴CQ=2CE=
∴BC+CQ=
∴t=秒．
综上所述：当t为11秒或12秒或秒时，为等腰三角形．
【点睛】本题考查了勾股定理的应用，线段的垂直平分线的性质，等腰三角形的性质，同时考查了等腰三角形中的分类讨论的思想，掌握以上知识是解题的关键.