

人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试单元测试同步达标检测题
展开
这是一份人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试单元测试同步达标检测题,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题
1、已知,则( )
A.B.C.D.
2、若,,且,,则的值是( )
A.B.C.或D.或
3、将函数的图象向左平移个单位长度得到的图象,则( )
A.B.的图象关于对称
C.D.的图象关于直线对称
4、已知函数在区间上单调递增,直线和为函数的图像的两条相邻对称轴,则( )
A.B.C.D.
5、已知函数,则( )
A.的最小正周期为B.的定义域为
C.若,则()D.在其定义域上是增函数
6、函数的图象由函数的图象向左平移个单位长度得到,则的图象与直线的交点个数为( )
A.1B.2C.3D.4
7、已知函数(,,)是奇函数,将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为.若的最小正周期为,且,则( )
A.B.C.D.2
8、函数,的图象与直线有且仅有两个不同的交点,则实数k的取值范围为( )
A.
B.
C.
D.
9、一根长的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移与时间的函数关系式是,其中g是重力加速度,当小球摆动的周期是时,线长l为( )
A.B.C.D.
10、已知函数,对于,,且在区间上单调递减,则的最大值是( )
A.B.C.D.
二、填空题
11、已知,,则________.
12、已知函数的部分图象如图所示,则满足条件的最小正整数x为_________.
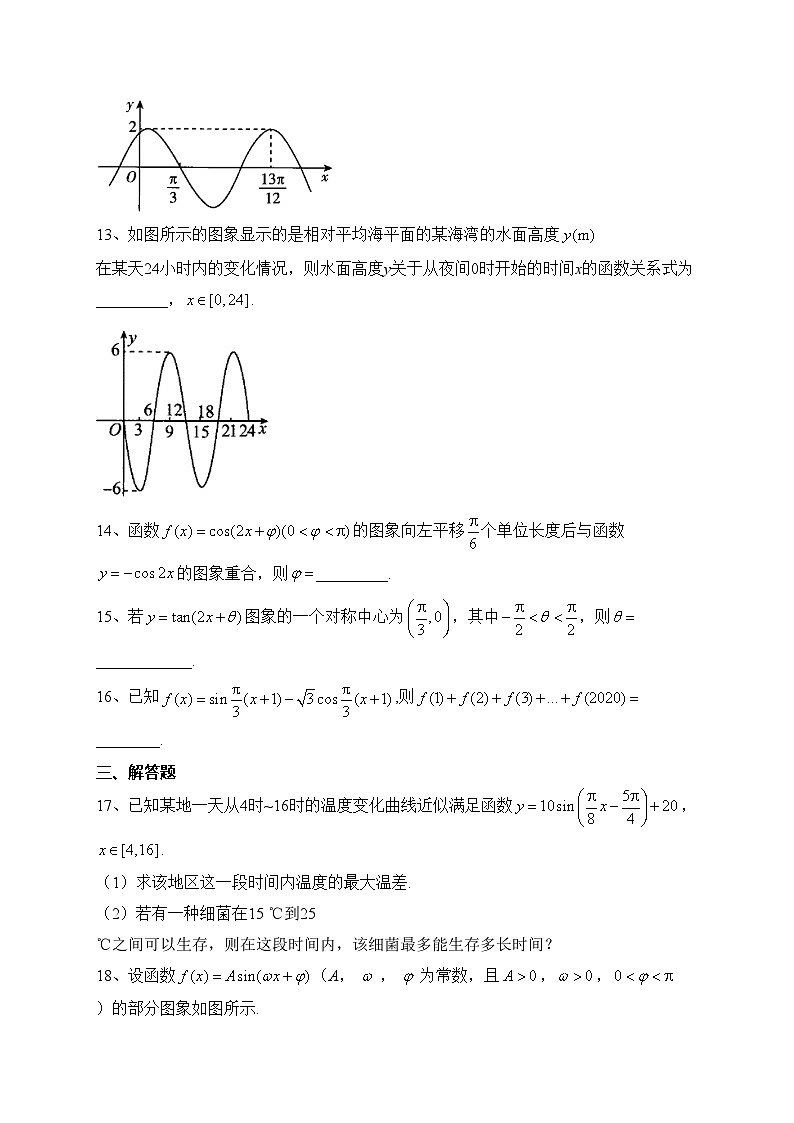
13、如图所示的图象显示的是相对平均海平面的某海湾的水面高度在某天24小时内的变化情况,则水面高度y关于从夜间0时开始的时间x的函数关系式为_________,.
14、函数的图象向左平移个单位长度后与函数的图象重合,则_________.
15、若图象的一个对称中心为,其中,则____________.
16、已知,则________.
三、解答题
17、已知某地一天从4时~16时的温度变化曲线近似满足函数,.
(1)求该地区这一段时间内温度的最大温差.
(2)若有一种细菌在15 ℃到25 ℃之间可以生存,则在这段时间内,该细菌最多能生存多长时间?
18、设函数(A,,为常数,且,,)的部分图象如图所示.
(1)求A,,的值;
(2)若存在,使得等式成立,求实数m的取值范围.
19、已知一个扇形的中心角是,所在圆的半径是R.
(1)若,,求扇形的面积;
(2)若扇形的周长为,面积为,求扇形圆心角的弧度数;
(3)若扇形的周长为定值C,当为多少弧度时,该扇形面积最大?并求出最大值.
20、已知在中,.
(1)求的值;
(2)判断是锐角三角形还是钝角三角形;
(3)求的值.
参考答案
1、答案:D
解析:,
,
则,
故选:D.
2、答案:B
解析:,,又,,,.又,,,于是,易得,则.
3、答案:B
解析:由题意,将函数的图象向左平移个单位长度,
可得,所以A不正确;
因为,所以的图象关于对称,所以B正确;
因为,所以C不正确;
令,,可得,,可得不是函数的对称轴,所以D不正确.故选B.
4、答案:D
解析:由题意得,解得,易知是的最小值点,所以,得,于是,则,故选D.
5、答案:ABC
解析:A,,函数的最小正周期为,故A正确;
B,由,,得,,
所以函数的定义域为,故B正确;
C,,得,,解得,,故C正确;
D,,,解得,,
所以函数在上单调递增,故D错误.
故选:ABC.
6、答案:C
解析:把函数的图象向左平移个单位长度后得到函数的图象.作出函数的部分图象和直线如图所示.观察图象知,共有3个交点.故选C.
7、答案:C
解析:由为奇函数,可知,由可得.将的图象上各点的横坐标伸长到原来的2倍,得的图象.由的最小正周期为,可得,所以,,可得,所以,则.故选C.
8、答案:C
解析:因为函数
当时,函数,当时,函数,作出函数的图象如图所示.
由图可知要使函数,的图象与直线有且仅有两个不同的交点,则有.
9、答案:D
解析:因为周期,所以,则.
10、答案:C
解析:由题意,在时取得最大值,
则,,即,.
又在区间上单调递减,
则,且,所以.
当时,得,所以的最大值为.故选C.
11、答案:
解析:,
,
,
,
,
,
故答案为:.
12、答案:2
解析:设函数的最小正周期为T,由图象可知,,所以,所以.当时,把点的坐标代入的解析式,得,所以,,则,;当时,将点的坐标代入的解析式,得,所以,,则.综上,,所以,,所以,所以或,所以或,所以或,,即或,,所以当时,x能取到的最小正整数为2.
13、答案:
解析:将题图图象看成,的图象,由图象知,,,.将点看成函数图象的第一个特殊点,则,.函数关系式为.
14、答案:
解析:,,因为平移后两函数图象重合,所以,.又,故.
15、答案:或
解析:由,得.图象的一个对称中心为,
令,得,.
又,或.
16、答案:
解析:,
函数的最小正周期为6,
,
,
故答案为:.
17、
(1)答案:
解析:由函数关系式易知,当时,函数取得最大值,此时温度最高,为,
当时,函数取得最小值,此时温度最低,为,
所以最大温差为.
(2)答案:小时
解析:令,得,
因为,所以.
令,得,
因为,所以.
故在这段时间内该细菌能存活的最长时间为(小时).
18、
(1)答案:,,
解析:根据函数(A,,为常数,且,,)的部分图象,
可得,,.
结合五点法作图可得,,解得,
函数.
(2)答案:
解析:存在,即存在,即存在,
使得等式成立,即成立.
令,即存在,使得直线和函数的图象有交点.
当时,,,
即实数m的取值范围为.
19、答案:(1)
(2)
(3)当时,扇形面积有最大值
解析:(1).
(2)由解得或18,
因为,所以.
(3)由得,
则,
当时,扇形面积有最大值.
20、
(1)答案:
解析:,①
两边平方,得,
.
(2)答案:钝角三角形
解析:由,且,
可知,A为钝角,是钝角三角形.
(3)答案:
解析:,
又,,,.②
由①②可得,,
.
相关试卷
这是一份高中数学人教B版 (2019)选择性必修 第三册第五章 数列本章综合与测试单元测试练习,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高中数学人教B版 (2019)必修 第三册第七章 三角函数本章综合与测试单元测试复习练习题,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份人教B版 (2019)必修 第二册第五章 统计与概率本章综合与测试单元测试当堂检测题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。










