高中数学苏教版 (2019)选择性必修第二册第6章 空间向量与立体几何本章综合与测试课后练习题

这是一份高中数学苏教版 (2019)选择性必修第二册第6章 空间向量与立体几何本章综合与测试课后练习题，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1、如图,在正三棱柱中,若,则点C到直线的距离为( )

A.B.C.D.
2、空间中有三点,,则点P到直线MN的距离为( )
A.B.C.D.
3、如图,在平行六面体中,设,,,则与向量相等的是( )
A.B.C.D.
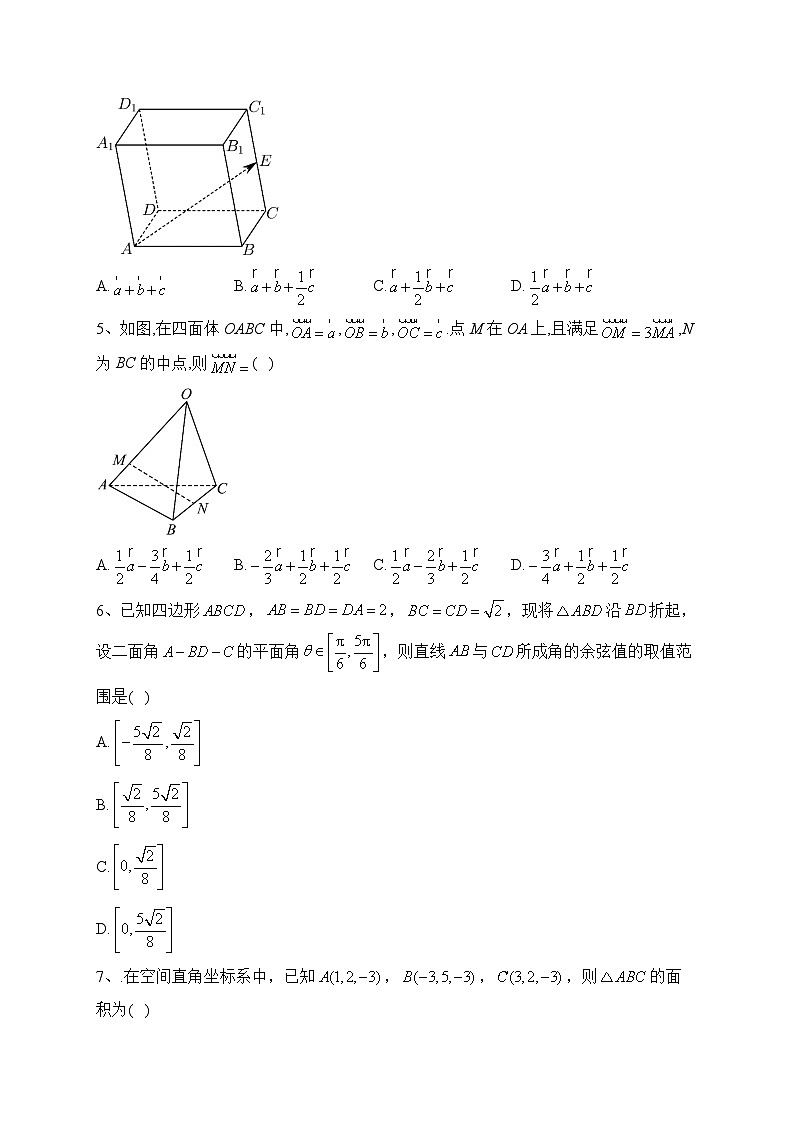
4、如图,平行六面体中,E为中点.设,,,用基底表示向量,则( )
A.B.C.D.
5、如图,在四面体OABC中,,,.点M在OA上,且满足,N为BC的中点,则( )
A.B.C.D.
6、已知四边形，，，现将沿折起，设二面角的平面角，则直线与所成角的余弦值的取值范围是( )
A.
B.
C.
D.
7、.在空间直角坐标系中，已知，，，则的面积为( )
A.1
B.2
C.3
D.4
8、如图，在棱长为2的正方体中，E为的中点，点P在线段上运动，则点P到直线的距离的最小值为( )
A.
B.
C.
D.
9、如图，在三棱锥中，，，，则异面直线与所成角的大小是( )
A.
B.
C.
D.
10、已知等腰直角三角形ABC,,点D为BC边上的中点,沿AD折起平面ABD使得,则异面直线AB与DC所成角的余弦值为( )
A.B.C.D.
二、填空题
11、在正方体中,E,F分别为棱AD,的中点,则异面直线与DF所成角的正弦值为________.
12、已知点,直线l过点,且l的一个方向向量为则点P到直线l的距离为____________.
13、已知向量,,若与的夹角为钝角,则实数t的取值范围为_____________.
14、已知直线l经过点,且其一个方向向量为,则直线l的方程为______________.
15、已知直线l的一个方向向量为，若点为直线l外一点，为直线l上一点，则点P到直线l的距离为___________.
16、如图所示，在长方体中，，，M是的中点，N是的中点，若异面直线与所成的角为，距离为d，则___________.
三、解答题
17、如图,在四棱锥中,平面平面ABCD,底面ABCD是矩形,O,E分别是BC,PA的中点,平面经过点O,D,E与棱PB交于点F．
（1）试用所学知识确定F在棱PB上的位置;
（2）若,求EF与平面PCD所成角的正弦值．
18、四棱柱的所有棱长都等于4，，平面平面，.
（1）证明：；
（2）在直线上是否存在点P，使平面？若存在，求出点P的位置；若不存在，请说明理由.
19、如图，在多面体中，平面平面，四边形为正方形，四边形为梯形，且，是边长为1的等边三角形，.
（1）求证：；
（2）线段上是否存在点N，使得直线平面？若存在，求出的值；若不存在，请说明理由.
20、如图，在直三棱柱中，，，M为棱的中点，N是的中点.
（1）证明：平面；
（2）求直线与平面所成角的正弦值.
参考答案
1、答案：B
解析：取AC的中点O,则,
以O为原点,,的方向分别为x,y轴的正方向建立空间直角坐标系,
则,,
所以,
所以在上的投影的长度为,
故点C到直线的距离．
故选：B.
2、答案：A
解析：,
则,,
则,
所以点P到直线MN的距离为.
故选：A.
3、答案：C
解析：因为,
所以.
故选：C.
4、答案：B
解析：.
故选：B.
5、答案：D
解析：如图,连接ON,
N是BC的中点,,
,,
.
故选：D.
6、答案：D
解析：如图，取的中点O，连接，，
，，
，，且，，
是二面角的平面角，
以O为坐标原点，，所在直线分别为x轴，y轴，过点O作平面的垂线为z轴，建立空间直角坐标系，则，，，
二面角的平面角，
，，
，
设与所成的角为，
则，
又，，
，
.
故直线与所成角的余弦值的取值范围是.
7、答案：C
解析：解法一：由，，，得，，，所以，，，
由余弦定理，得，所以，所以的面积为.
解法二：由，，，得，，
所以，，
故点C到直线的距离，则的面积为.
8、答案：A
解析：以D为原点，，，分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，
则，，，，，，.
解法一：设异面直线与的公垂线段的方向向量为，则，，
即令，则，，，
异面直线与之间的距离，
点P在线段上运动，
点P到直线的距离的最小值为.
解法二：设，，，则，所以即，所以，又，，
点P到直线的距离，
当且仅当时，，点P到直线的距离的最小值为.故选A.
9、答案：B
解析：，，
.
，，
.
又，
，
，
异面直线与所成角的大小为.
10、答案：B
解析：已知等腰直角三角形ABC,点D是BC中点,则,
沿着AD翻折平面ADB可得,
所以,
又,BD,平面BCD,
所以平面BCD,
不妨设,则,
以,,为基底的空间向量,
所以,
则
所以,
因为AB,DC是异面直线,所以异面直线AB,DC的余弦值为.
故选：B.
11、答案：
解析：如图所示,建立空间直角坐标系,
设正方体的棱长为2,则,,,,
则,,
,
所以与DF所成角的正弦值为.
故答案为:.
12、答案：
解析：易知,所以点P到直线l的距离为.
故答案为：.
13、答案：
解析：由;
由.
综上：且.
故答案为：.
14、答案：
解析：因为直线l的一个方向向量为,
则直线的斜率,又直线过点,
故所求直线方程为,即.
故答案为：.
15、答案：
解析：由题知，
，
，
，
又，
点P到直线l的距离为.
16、答案：
解析：建立空间直角坐标系，如图所示：
则，，，，所以，，
所以，即，所以.
设与，都垂直的一个向量为，
则即
解得所以，
又，
所以，
所以.
17、答案：（1）见解析
（2）
解析：（1）过P作直线l与BC平行,延长DE与l交于点G,
连接OG,OG与PB的交点即为点F．
因为底面ABCD是矩形,O是BC的中点,
所以,且．
又,所以,
因为E是PA的中点,可得,
则,所以．
故F在棱PB的靠近B的三等分点处．
（2）因为,O是BC的中点,所以,
又平面平面ABCD,平面平面,
平面PBC,所以平面ABCD．
取AD中点Q,连接OQ,易知OQ,OC,OP两两相互垂直,
如图,分别以OQ,OC,OP为x,y,z轴建立空间直角坐标系,
则,,,,,
,,．

设平面PCD的法向量为,
则即令,
则,所以．
．
设EF与平面PCD所成角为,
则,
所以EF与平面PCD所成角的正弦值为．
18、答案：（1）证明见解析
（2）点P在的延长线上且使的位置
解析：（1）证明：设交于点O，则，连接.
在中，，，，
，
，，
又平面平面，平面平面，
底面.
以O为坐标原点，，，所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，
则，，，，，，
，，，
（2）假设在直线上存在点P，使平面.设，,
则，，.
易得，.
设平面的一个法向量为，
则即
令，则，，.
平面，，
，解得，
即点P在的延长线上且使的位置.
19、答案：（1）证明见解析
（2）所以不存在点N，使得直线平面
解析：（1）证明：因为四边形为正方形，所以.
又平面平面，且平面平面，所以平面.
又平面，所以.
（2）线段上不存在点N，使得直线平面.理由如下：取的中点O，的中点K，连接，，
因为为等边三角形，所以，
在正方形中，，
又平面平面，平面平面，
所以平面，
所以，
所以，，两两互相垂直，
以O为原点，，，所在直线分别为x轴，y轴，z轴建立空间直角坐标系，如图所示，
则，，，，
，，
所以，，.
设，，，
所以，
所以所以
即，
所以.
设平面AFN的一个法向量为，
则
所以
令，则，
所以.
因为平面，所以，
所以，此方程无解，
所以不存在点N，使得直线平面.
20、答案：（1）证明见解析
（2）
解析：（1）证明：连接，过点M作，交于点E，因为，M为棱的中点，所以，
因为三棱柱为直三棱柱，
所以平面，
又，平面，
所以，，
故，，两两互相垂直，
以M为坐标原点，，，所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，
因为，
所以，
由勾股定理，得，
所以，，，，，，
则，，，
设平面的一个法向量为，
则
令，则，，
所以，
因为，
所以，
因为平面，
所以平面.
（2）由（1）得，，，，
设平面的一个法向量为，
则
令，则，，
所以，
设直线与平面所成的角为，
则
，
故直线与平面所成角的正弦值为.