2023-2024学年北京市怀柔区名校八上数学期末学业水平测试试题含答案

这是一份2023-2024学年北京市怀柔区名校八上数学期末学业水平测试试题含答案，共7页。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
1．将数据0.0000025用科学记数法表示为（ ）
A．B．C．D．
2．下列各式能用平方差公式计算的是（ ）
A．B．
C．D．
3．把分解因式，结果正确的是( )
A．B．
C．D．
4．如图，，，，下列条件中不能判断的是（ ）
A．B．C．D．
5．如图，在小正三角形组成的网格中，已有7个小正三角形涂黑，还需要涂黑个小正三角形，使它们和原来涂黑的小正三角形组成新的图案既是轴对称图形又是中心对称图形，则的最小值为( )
A．3B．4C．5D．6
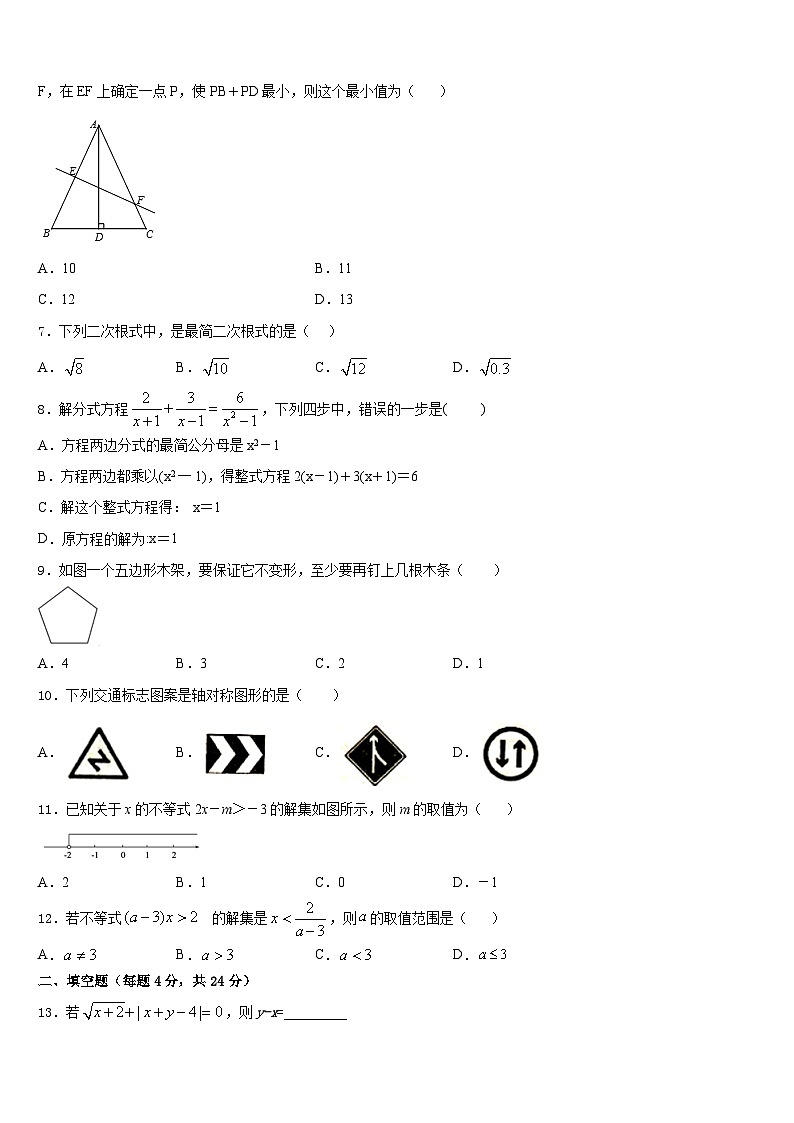
6．如图，在△ABC中，AB＝AC，BC＝10，S△ABC＝60，AD⊥BC于点D，EF垂直平分AB，交AB于点E，AC于点F，在EF上确定一点P，使PB＋PD最小，则这个最小值为（ ）
A．10B．11
C．12D．13
7．下列二次根式中，是最简二次根式的是（ ）
A．B．C．D．
8．解分式方程，下列四步中，错误的一步是( )
A．方程两边分式的最简公分母是x2－1
B．方程两边都乘以(x2一1)，得整式方程2(x－1)＋3(x＋1)＝6
C．解这个整式方程得： x＝1
D．原方程的解为:x＝1
9．如图一个五边形木架，要保证它不变形，至少要再钉上几根木条（ ）
A．4B．3C．2D．1
10．下列交通标志图案是轴对称图形的是（ ）
A．B．C．D．
11．已知关于x的不等式2x－m＞－3的解集如图所示，则m的取值为（ ）
A．2B．1C．0D．－1
12．若不等式的解集是，则的取值范围是（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．若，则y-x=_________
14．若（m+1）0＝1，则实数m应满足的条件_____．
15．已知一次函数y=（-1-a2）x+1的图象过点（x1，2），（x2-1），则x1与x2的大小关系为______．
16．如果△ABC的三边长分别为7，5，3，△DEF的三边长分别为2x﹣1，3x﹣2，3，若这两个三角形全等，则x=__________．
17．分解因式：4mx2﹣my2=_____．
18．我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图，此表揭示了（a+b）n（n为非负整数）展开式的各项系数的规律，例如：（a+b）0＝1，它只有一项，系数为1；（a+b）1＝a+b，它有两项，系数分别为1，1；（a+b）2＝a2+2ab+b2，它有三项，系数分别为1，2，1；（a+b）3＝a3+3a2b+3ab2+b3，它有四项，系数分别为1，3，3，1；…；根据以上规律，（a+b）5展开式共有六项，系数分别为______，拓展应用：（a﹣b）4＝_______．
三、解答题（共78分）
19．（8分）已知一次函数的解析式为，求出关于轴对称的函数解析式.
20．（8分）已知：如图，相交于点．
求证：
21．（8分）求不等式组的正整数解．
22．（10分）（列二元一次方程组求解）班长安排小明购买运动会的奖品，下面对话是小明买回奖品时与班长的对话情境：
小明说：“买了两种不同的笔记本共50本，单价分别是5元和9元，我给了400元，现在找回88元．”
班长说：“你肯定搞错了．”
小明说：“我把自己口袋里的18元一起当作找回的钱款了．”
班长说：“这就对啦！”
请根据上面的信息，求两种笔记本各买了多少本？
23．（10分）如图，是等边三角形，点在上，点在的延长线上,且．
(1)如图甲，若点是的中点，求证：
(2)如图乙，若点不的中点，是否成立?证明你的结论．
(3)如图丙，若点在线段的延长线上，试判断与的大小关系，并说明理由．
24．（10分）列分式方程解应用题：北京第一条地铁线路于1971年1月15日正式开通运营．截至2017年1月，北京地铁共有19条运营线路，覆盖北京市11个辖区．据统计，2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍，2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时，求2017年地铁每小时的客运量．
25．（12分） “转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数；
(2)若对图(1)中星形截去一个角，如图(2)，请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；
(3)若再对图(2)中的角进一步截去，你能由题(2)中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程)
26．（12分）如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D．
求证：AD=BC．
参考答案
一、选择题（每题4分，共48分）
1、D
2、C
3、C
4、B
5、C
6、C
7、B
8、D
9、C
10、B
11、D
12、C
二、填空题（每题4分，共24分）
13、8
14、m≠﹣1
15、x1＜x1
16、1
17、m（2x+y）（2x﹣y）
18、1，5，10，10，5，1 a4﹣4a3b+6a2b2﹣4ab3+b4
三、解答题（共78分）
19、y= -2x-1
20、见解析
21、不等式组的正整数解为：1，2，3
22、两种笔记本各买30本，20本
23、（1）详见解析；（2）成立，理由详见解析；（3），证明详见解析.
24、24万人．
25、（1）180°；（2）360°；（3）1080°．
26、证明见解析．