甘肃省白银市2023-2024学年九年级上学期期末数学试题

这是一份甘肃省白银市2023-2024学年九年级上学期期末数学试题，共12页。试卷主要包含了请将各题答案填在答题卡上等内容，欢迎下载使用。

注意事项：
1.本试卷共150分，考试时间120分钟。
2.请将各题答案填在答题卡上。
一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项.
1.下面四个关系式中，y是x的反比例函数的是（ ）
A.B.
C.D.
2.先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源，下图是喜庆集会时击鼓瞬间的情景及鼓的立体图形，该立体图形的主视图是（ ）
3.如图，这是某商店售卖的花架简图，其中，，，，则的长为（ ）
A.B.C.D.
4.如图，建筑公司验收门框时要求是矩形，在中，对角线，相交于点O，下列验算方法错误的是（ ）
A.B.C.D.
5.若关于x的一元二次方程的一个解是，则的值是（ ）
A.2021B.2024C.2026D.2027
6.如图，在平面直角坐标系中，菱形的顶点D在x轴上，边在y轴上，若点A的坐标为，则C点的坐标为（ ）
A.B.C.D.
7.甲、乙两名同学在一次用频率估计概率的试验中，统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（ ）
A.掷一枚正六面体的骰子，出现1点的概率
B.抛一枚硬币，出现正面的概率
C.任意写一个整数，它能被3整除的概率
D.从一个装有2个白球和1个红球的袋子中任取一球，取到白球的概率
8.图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现.图2是该台灯的电流与电阻成反比例函数的图象，该图象经过点.根据图象可知，下列说法正确的是（ ）
A.当时，
B. I与R的函数关系式是
C.当时，
D.当时，I的取值范围是
9.如图，在矩形中，，，点E，F分别在边，上，，，交于点G，若G是的中点，则的长是（ ）
A.5B.6C.6.4D.7.2
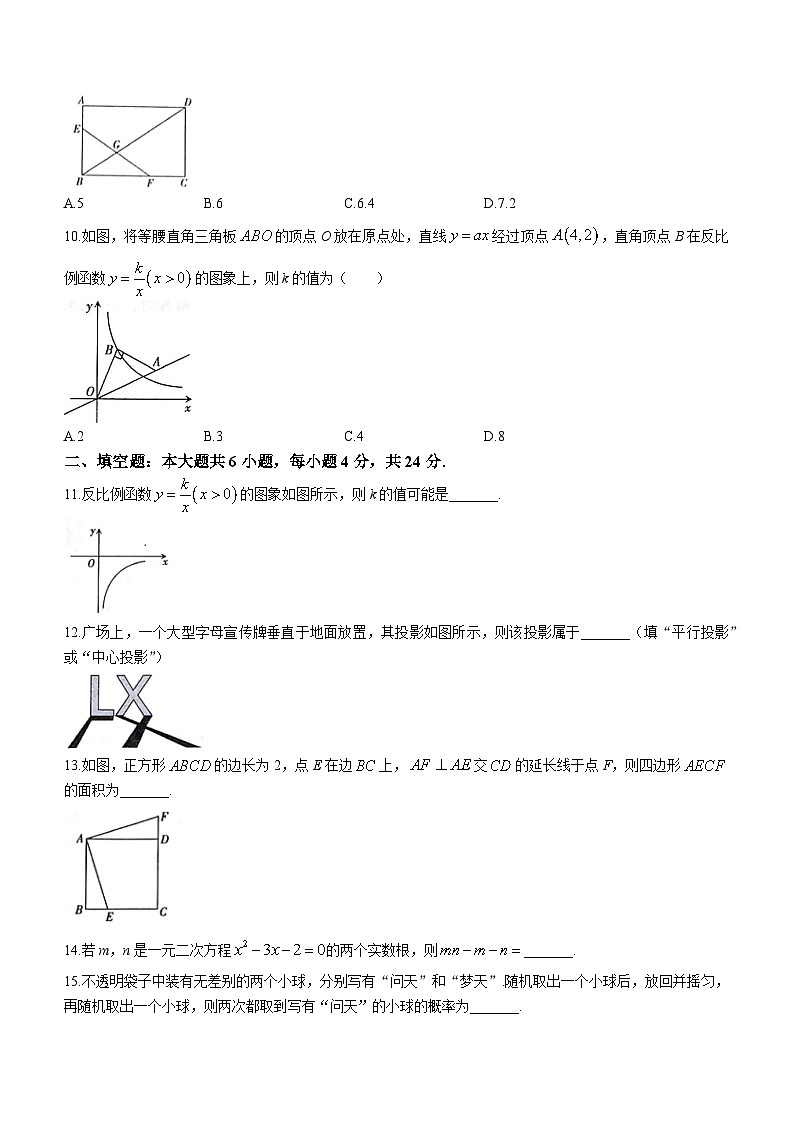
10.如图，将等腰直角三角板的顶点O放在原点处，直线经过顶点，直角顶点B在反比例函数的图象上，则k的值为（ ）
A.2B.3C.4D.8
二、填空题：本大题共6小题，每小题4分，共24分.
11.反比例函数的图象如图所示，则k的值可能是_______.
12.广场上，一个大型字母宣传牌垂直于地面放置，其投影如图所示，则该投影属于_______（填“平行投影”或“中心投影”）
13.如图，正方形的边长为2，点E在边上，交的延长线于点F，则四边形的面积为_______.
14.若m，n是一元二次方程的两个实数根，则_______.
15.不透明袋子中装有无差别的两个小球，分别写有“问天”和“梦天”.随机取出一个小球后，放回并摇匀，再随机取出一个小球，则两次都取到写有“问天”的小球的概率为_______.
16.一组正方形按如图所示的方式放置，其中顶点在y轴上，顶点，，，，，，…在x轴上，已知正方形的边长为1，，…，则正方形的边长是_______.
三、解答题：本大题共6小题，共46分.解答时，应写出必要的文字说明、证明过程或演算步骤.
17.（6分）解方程：.
18.（6分）小雨在参观故宫博物院时，被太和殿窗棂的三交六椀菱花图案所吸引，他从中提取出一个含60°角的菱形（如图所示）.若的长度为a，求菱形的面积.
19.（6分）如图，点D，E分别在的边，上，.求证：.
20.（8分）如图，有4张除了正面图案不同，其余都相同的卡片.
（1）这四张卡片上的立体图形中，主视图是矩形的有________（填字母序号）；
（2）将这四张卡片背面朝上混合均匀，从中随机抽出一张后放回，混合均匀后再随机抽出一张，求两次抽出的卡片上的立体图形的主视图都是矩形的概率.
21.（10分）已知关于x的一元二次方程.
（1）若该方程的一个根是，求m的值及方程的另一个根.
（2）求证：无论m取何值，该方程总有两个实数根.
22.（10分）如图，一次函数与反比例函数的图象在第一象限交于和两点，与x轴交于点C.
（1）求反比例函数和一次函数的解析式；
（2）连接，，求的面积.
四.解答题：本大题共5小题，共50分.解答时，应写出必要的文字说明、证明过程或演算步骤.
23.（8分）在边长为1的正方形中，点E在边上（不与点A，D重合），射线与射线交于点F.
（1）若，求的长.
（2）求证：.
24.（10分）白银市某商城在2024年元旦期间促销某品牌冰箱，每台进货价为2500元，标价为3000元.
（1）商城举行了“元旦回馈新老用户”摸奖活动，将冰箱连续两次降价，每次降价的百分率相同，最后以2430元售给中奖者，求每次降价的百分率.
（2）市场调研表明：当每台售价为2900元时，平均每天能售出8台，当每台售价每降50元时，平均每天就能多售出4台.若商城要想使该冰箱的销售利润平均每天达到5000元，则每台冰箱的定价应为多少元?
25.（10分）喝茶前需要烧水和泡茶两个工序，电热水壶将水烧到100℃，然后继续加热1分钟后断电，烧水时水温y（℃）与时间x（min）成一次函数关系；断电后，水壶中水的温度（℃）与时间x（min）近似于反比例函数关系（如图）.已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃.
（1）分别求出图中段和段所对应的函数关系式.
（2）从水壶中的水烧开（100℃）降到80℃就可以进行泡茶，问从水烧开到泡茶需要等待多长时间?
26.（10分）如图，将矩形沿折叠，使点D落在边的点E处，过点E作交于点G，连接.
（1）求证：四边形是菱形.
（2）试证明.
27.（12分）如图1，四边形为正方形，点A在y轴上，点B在x轴上，且，反比例函数在第一象限的图象经过正方形的顶点C.
（1）求点C的坐标.
（2）如图2，将正方形沿x轴向右平移得到正方形，点恰好落在反比例函数的图象上，求此时点的坐标.
（3）在（2）的条件下，点P为y轴上一动点，平面内是否存在点Q，使以点O，，P，Q为顶点的四边形为菱形?若存在，请直接写出点Q的坐标；若不存在，请说明理由.
白银市2023—2024学年度九年级第一学期期末诊断考试
数学参考答案
11.（答案不唯一）
12.中心投影
13.4
14.
15.
16.
17.解：整理，得，
，，，
，
.
，.
18.解：如图，过点A作于点H，
四边形是菱形，
，
是等边三角形，
，
菱形的面积.
19.证明：，
在和中，
，，
.
20.解：（1）A，D.
（2）列表可得
由表可知，共有16种等可能的结果，其中两次抽出的卡片上的立体图形的主视图都是矩形的有4种，所以两次抽出的卡片上的立体图形的主视图都是矩形的概率为.（8分）
21.解：（1）是方程的一个根，
，
解得.
则原方程为.
解得，.
即方程的另一个根为.（5分）
（2）证明：，
无论m取何值，该方程总有两个实数根.（10分）
22.解：（1）点在反比例函数的图象上，
，
反比例函数的解析式为，
又在反比例函数的图象上，
，点，
由于直线过点，，
解得
一次函数的解析式为.
（2）如图，分别过点A，B作x轴的垂线，垂足为D，E，
直线与x轴的交点，即，
.
23.解：（1）由题意得
，
.
，.
（2）证明：由题意得，.
又，.
.
，
.
24.解：（1）设每次降价的百分率为x，
依题意得
解得，（不合题意，舍去）.
答：每次降价的百分率是10%.（4分）
（2）设每台售价下调元，
依题意得
解得.
所以下调150元，因此定价为2750元.（10分）
25.解：（1）停止加热时，设，
由题意得，解得，
，
当时，解得，
C点坐标为，B点坐标为，
当加热烧水时，设，
由题意得，解得，
当加热烧水时，y与x的函数关系式为
故段对应的函数关系式为，段对应的函数关系式为.
（2）把代入，得，
因此从水烧开到泡茶需要等待（min）.
26.证明：（1），
由翻折的性质可知，，，
，.
.
四边形为菱形.（4分）
（2）如图，连接，交于点O.
四边形为菱形，，.
，，.
，即.
，，.
又，
.
27.解：（1）作轴于H.
四边形是正方形，，，，
，，，
，，
反比例函数在第一象限的图象经过正方形的顶点C，
，即，解得.
点C的坐标为.
（2）由（l）同理可得点，
点恰好落在反比例函数的图象上，
当时，，
，即.（6分）
（3）当时，如图，
当点Q在第一象限时，，，
四边形是菱形，
，，.
当点Q在第四象限时，.
当时，如图，
则点与Q关于y轴对称，.
当时，如图，设，
则，，解得，
，.
综上，或或或.1
2
3
4
5
6
7
8
9
10
C
B
D
D
D
B
C
D
B
B
A
B
C
D
A
B
C
D