2023-2024学年安徽省清华附中合肥学校九年级（上）段考数学试卷（12月份）（含解析）

这是一份2023-2024学年安徽省清华附中合肥学校九年级（上）段考数学试卷（12月份）（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.抛物线的解析式y=−2x2−1，则顶点坐标是( )
A. (−2,−1)B. (2,1)C. (0,−1)D. (0,1)
2.已知ab=23，则代数式a+bb的值为( )
A. 52B. 53C. 23D. 32
3.在Rt△ABC中，∠C=90°，sinA=35，BC=6，则AB长是( )
A. 4B. 6C. 8D. 10
4.如果反比例函数y=a−2x(a是常数)的图象在第一、三象限，那么a的取值范围是( )
A. a0C. a2
5.将抛物线y=x2−2x+1向下平移2个单位，再向左平移1个单位，所得抛物线的解析式是
( )
A. y=x2−2x−1B. y=x2+2x−1C. y=x2−2D. y=x2+2
6.如图，点P是▱ABCD边AB上的一点，射线CP交DA的延长线于点E，则图中相似的三角形有( )
A. 0对B. 1对C. 2对D. 3对
7.已知二次函数y=ax2+bx+c中y与x的部分对应值如下表，下列说法正确的是：( )
A. 抛物线开口向上
B. 其图象的对称轴为直线x=1
C. 当x0)的图象上，则经过点B的反比例函数解析式为( )
A. y=−6x
B. y=−4x
C. y=−2x
D. y=2x
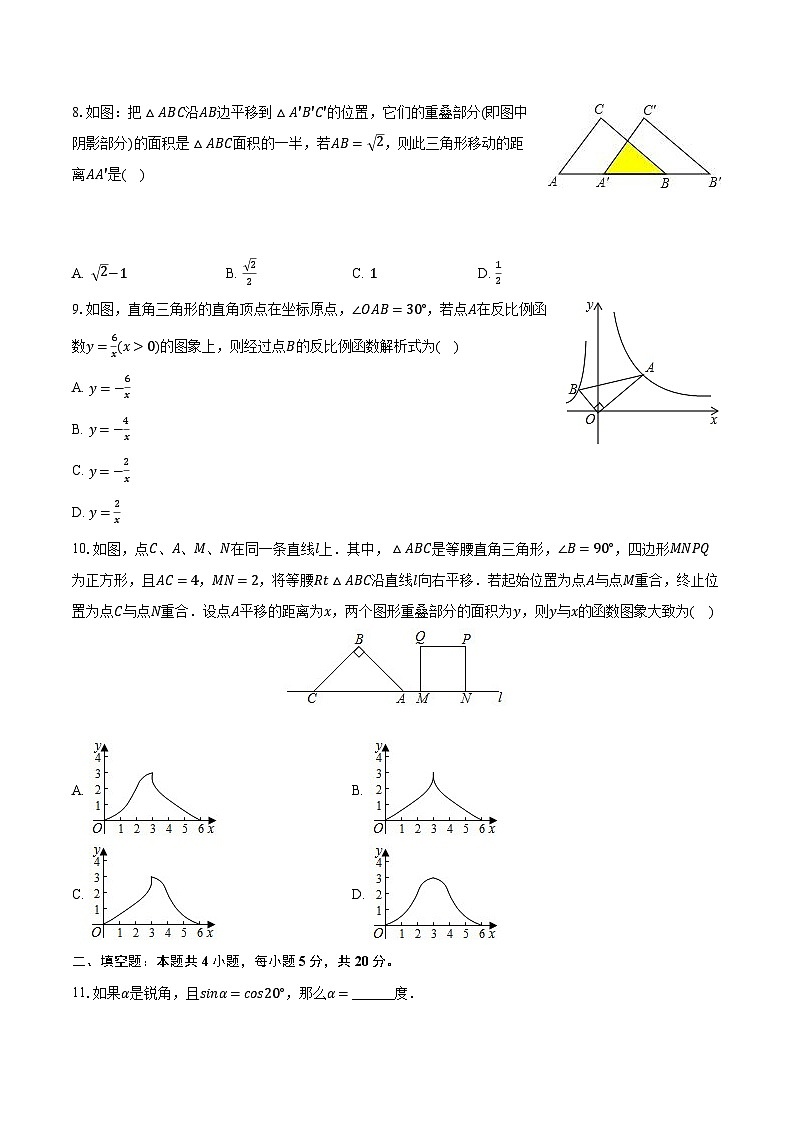
10.如图，点C、A、M、N在同一条直线l上．其中，△ABC是等腰直角三角形，∠B=90°，四边形MNPQ为正方形，且AC=4，MN=2，将等腰Rt△ABC沿直线l向右平移．若起始位置为点A与点M重合，终止位置为点C与点N重合．设点A平移的距离为x，两个图形重叠部分的面积为y，则y与x的函数图象大致为( )
A. B.
C. D.
二、填空题：本题共4小题，每小题5分，共20分。
11.如果α是锐角，且sinα=cs20°，那么α=______度．
12.已知△ABC∽△A′B′C′，AB=2，A′B′=6，则△ABC与△A′B′C′的周长之比为______ ．
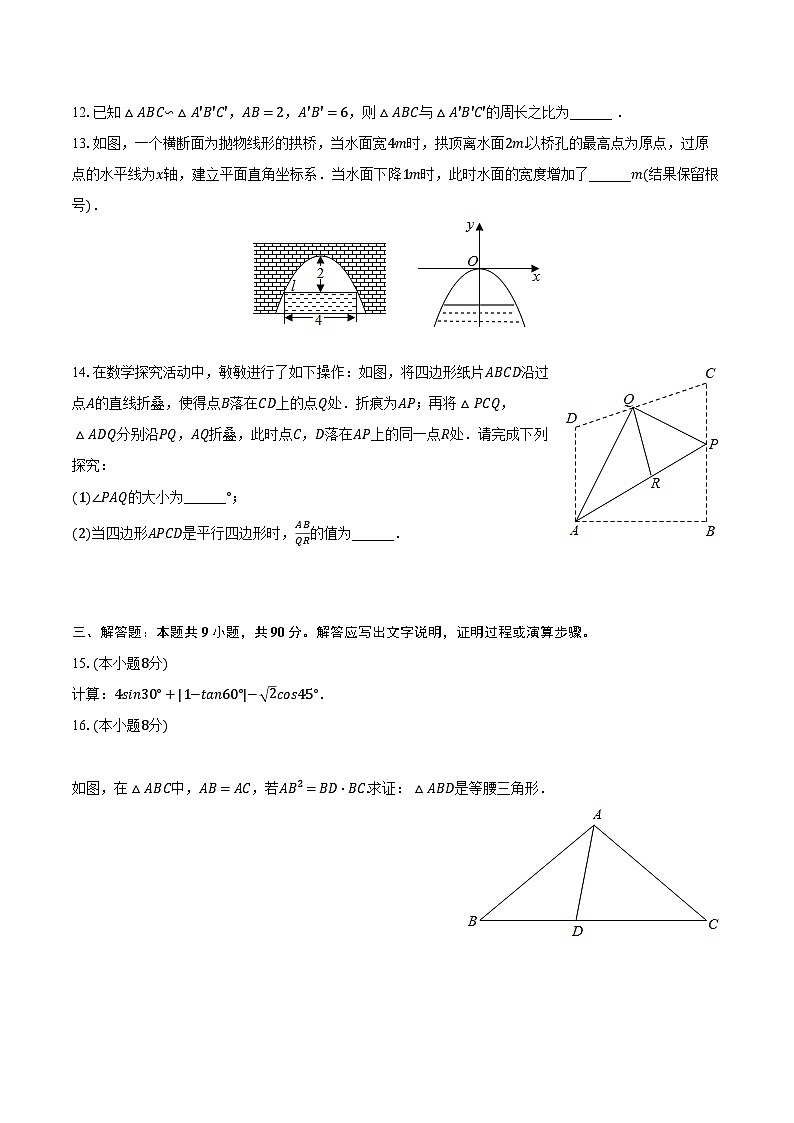
13.如图，一个横断面为抛物线形的拱桥，当水面宽4m时，拱顶离水面2m.以桥孔的最高点为原点，过原点的水平线为x轴，建立平面直角坐标系．当水面下降1m时，此时水面的宽度增加了______m(结果保留根号)．
14.在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片ABCD沿过点A的直线折叠，使得点B落在CD上的点Q处．折痕为AP；再将△PCQ，△ADQ分别沿PQ，AQ折叠，此时点C，D落在AP上的同一点R处．请完成下列探究：
(1)∠PAQ的大小为______°；
(2)当四边形APCD是平行四边形时，ABQR的值为______．
三、解答题：本题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
计算：4sin30°+|1−tan60°|− 2cs45°．
16.(本小题8分)
如图，在△ABC中，AB=AC，若AB2=BD⋅BC.求证：△ABD是等腰三角形．
17.(本小题8分)
如图所示，在△ABC中，∠C=90°，D是BC的中点，DE⊥AB于点E，tanB=12，AC=5，求DE的长．
18.(本小题8分)
方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示，解答问题：
(1)请按要求对△OAB作变换：以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA′B′．
(2)写出点A′的坐标______；
(3)△OA′B′的面积为______．
19.(本小题10分)
如图，某建筑物CD高96米，它的前面有一座小山，其斜坡AB的坡度为i=1：1.为了测量山顶A的高度，在建筑物顶端D处测得山顶A和坡底B的俯角分别为α、β.已知tanα=2，tanβ=4，求山顶A的高度AE(C、B、E在同一水平面上)．
20.(本小题10分)
如图，已知二次函数y=x2+mx+n的图象经过A(0,3)，且对称轴是直线x=2．
(1)求该函数解析式；
(2)在抛物线上找点P，使△PBC的面积是△ABC的面积的23，求出点P的坐标．
21.(本小题12分)
如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y=kx(k>0,x>0)的图象上，点D的坐标为(4,3)，设AB所在直线解析式为y=ax+b(a≠0)．
(1)求k的值，并根据图象直接写出关于x的不等式ax+b>kx的解集；
(2)若将菱形ABCD沿x轴正方向平移m个单位在平移中，若反比例函数图象与菱形的边AD始终有交点，求m的取值范围．
22.(本小题12分)
襄阳市某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种产品的成本为30元/件，且年销售量y(万件)关于售价x(元/件)的函数解析式为：y=−2x+140(40≤x0，
∴a>2．
故选：D．
反比例函数y=kx图象在一、三象限，可得k>0．
本题运用了反比例函数y=kx图象的性质，关键要知道k的决定性作用．
5.【答案】C
【解析】解：根据题意y=x2−2x+1=(x−1)2向下平移2个单位，再向左平移1个单位，得y=(x−1+1)2−2，y=x2−2．
故选：C．
抛物线y=x2−2x+1化为顶点坐标式再按照“左加右减，上加下减”的规律平移则可．
此题不仅考查了对平移的理解，同时考查了学生将一般式转化顶点式的能力．
6.【答案】D
【解析】【分析】
利用相似三角形的判定方法以及平行四边形的性质得出即可．
此题主要考查了相似三角形的判定以及平行四边形的性质，熟练掌握相似三角形的判定方法是解题关键．
【解答】
解：∵四边形ABCD是平行四边形，
∴AB/​/DC，AD//BC，
∴△EAP∽△EDC，△EAP∽△CBP，
∴△EDC∽△CBP，
故有3对相似三角形．
故选D．
7.【答案】C
【解析】解：把(−1,−3)，(0,1)，(1,3)代入y=ax2+bx+c得a−b+c=−3c=1a+b+c=3，解得a=−1b=3c=1，
∴抛物线解析式为y=−x2+3x+1，
∴ y=−(x−32)2+134，
∴抛物线开口向下，对称轴为直线x=32，当x