








2024 年沈阳市高中三年级教学质量监测数学试卷及参考答案
展开
这是一份2024 年沈阳市高中三年级教学质量监测数学试卷及参考答案,文件包含2024数学市一模试题docx、2024数学市一模试题pdf、2024数学市一模答案docx、2024数学市一模答案pdf等4份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
命题: 沈阳市第二十七中学 李 刚
沈阳市第十一中学 代 晶
沈阳市第二中学 季爱民
主审: 沈阳市教育研究院 王孝宇
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.
注意事项:
答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条码粘贴在答题卡指定区域.
第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动用橡皮擦干净后,再选涂其他答案标号.第Ⅱ卷用黑色墨水签字笔在答题卡指定位置书写作答,在本试题卷上作答无效.
3.考试结束后,考生将答题卡交回.
第Ⅰ卷(选择题 共60分)
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,集合,,则( )
2. 设复数满足,则=( )
1
3. 曲线在点处的切线方程为( )
4. 已知单位向量,满足,则( )
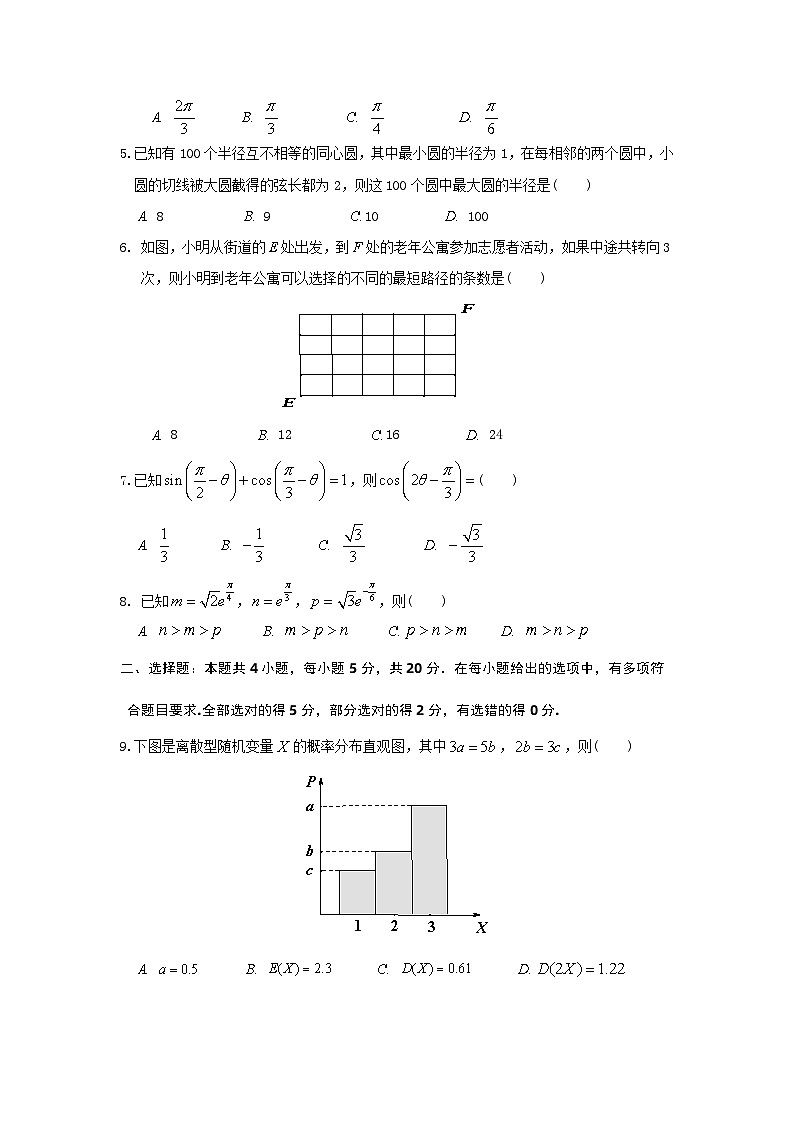
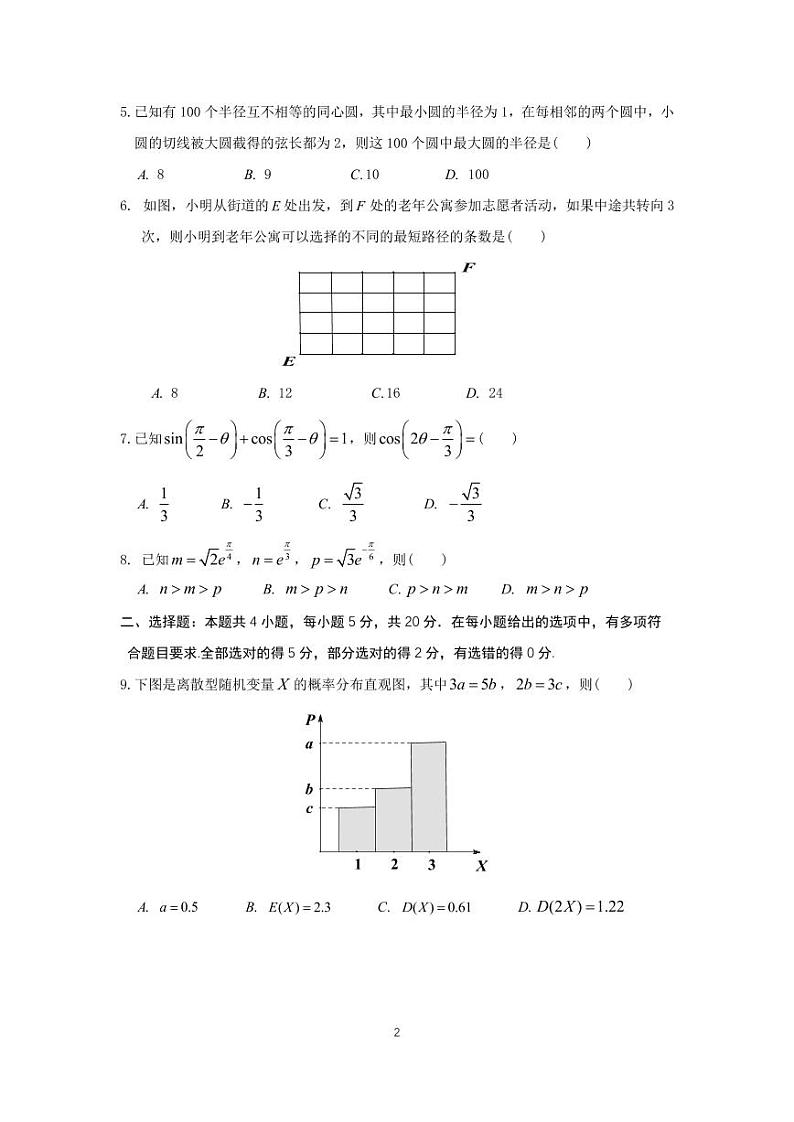
5.已知有100个半径互不相等的同心圆,其中最小圆的半径为1,在每相邻的两个圆中,小圆的切线被大圆截得的弦长都为2,则这100个圆中最大圆的半径是( )
8 9 10 100
6. 如图,小明从街道的处出发,到处的老年公寓参加志愿者活动,如果中途共转向3次,则小明到老年公寓可以选择的不同的最短路径的条数是( )
8 12 16 24
7.已知,则( )
8. 已知,,,则( )
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下图是离散型随机变量的概率分布直观图,其中,,则( )
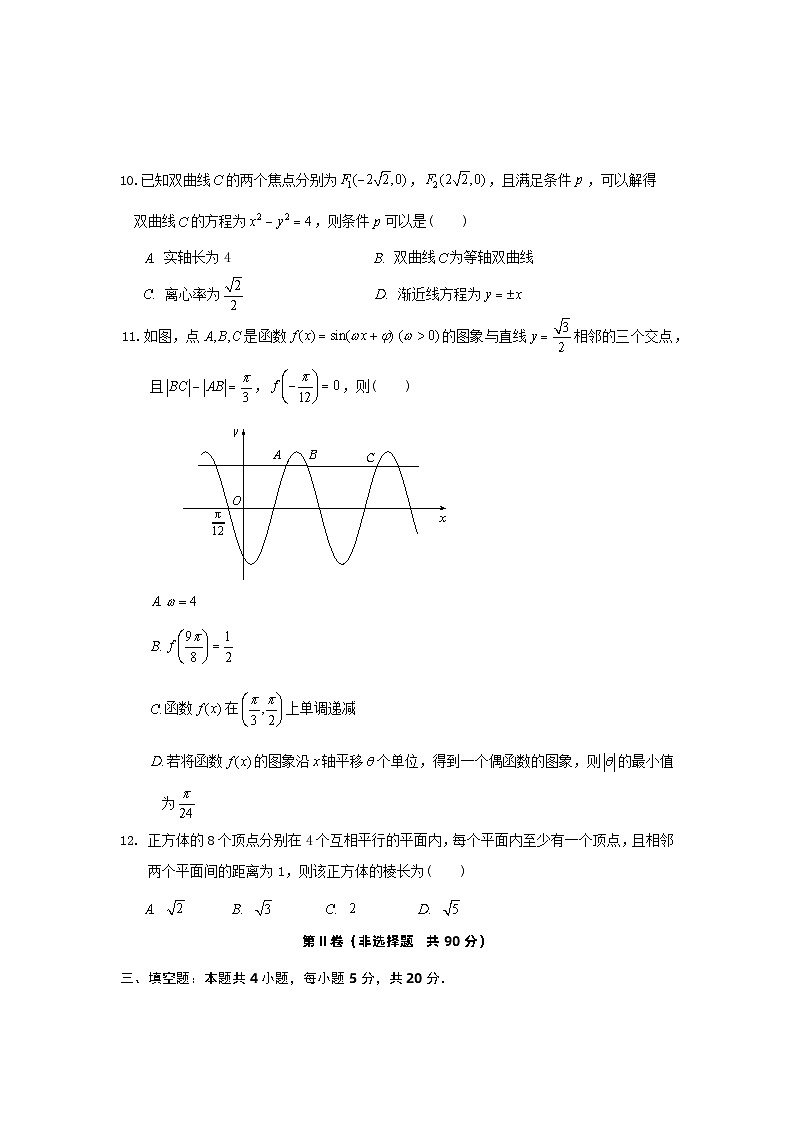
10.已知双曲线的两个焦点分别为,,且满足条件,可以解得
双曲线的方程为,则条件可以是( )
实轴长为4 双曲线为等轴双曲线
离心率为 渐近线方程为
11.如图,点是函数的图象与直线相邻的三个交点,且,,则( )
函数在上单调递减
若将函数的图象沿轴平移个单位,得到一个偶函数的图象,则的最小值为
12. 正方体的8个顶点分别在4个互相平行的平面内,每个平面内至少有一个顶点,且相邻两个平面间的距离为1,则该正方体的棱长为( )
第Ⅱ卷(非选择题 共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13. 的展开式中常数项的二项式系数为 .
14.已知抛物线的焦点为,若点是抛物线上到点距离最近的点,则
.
15.的一个充分不必要条件是 .
16. 已知是半径为1的球面上不同的三点,则的最小值为 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知等比数列的各项均为正数,且,.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求证:.
18. (12分)
在中,角所对的边分别为,且.
(Ⅰ)求证:;
(Ⅱ)当取最小值时,求的值.
19. (12分)
如图,在三棱锥中,平面平面,且,
,点在线段上,点在线段上.
(Ⅰ)求证:;
(Ⅱ)若平面,求的值;
(Ⅲ)在(Ⅱ)的条件下,求平面与平面所成角的余弦值.
20. (12分)
某城市有甲,乙两个网约车公司,相关部门为了更好地监管和服务,通过问卷调查的方式,统计当地网约车用户(后面简称用户,并假设每位用户只选择其中一家公司的网约车出行)对甲,乙两个公司的乘车费用,等待时间,乘车舒适度等因素的评价,得到如下统计结果:
= 1 \* GB3 ①用户选择甲公司的频率为0.32,选择乙公司的频率为0.68;
= 2 \* GB3 ②选择甲公司的用户对等待时间满意的频率为0.62,选择乙公司的用户对等待时间满意的
频率为0.78;
= 3 \* GB3 ③选择甲公司的用户对乘车舒适度满意的频率为0.68,选择乙公司的用户对乘车舒适度满
意的频率为0.61;
= 4 \* GB3 ④选择甲公司的用户对乘车费用满意的频率为0.21,选择乙公司的用户对乘车费用满意的频率为0.32.
将上述随机事件发生的频率视为其发生的概率.
(Ⅰ)分别求出网约车用户对等待时间满意,乘车舒适度满意,乘车费用满意的概率,并比较用户对哪个因素满意的概率最大,对哪个因素满意的概率最小.
(Ⅱ)若已知某位用户对乘车舒适度满意,则该用户更可能选择哪个公司的网约车出行?并说明理由.
21. (12分)
已知如图,点为椭圆的短轴的两个端点,且的坐标为,椭圆的离心率
为.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线不经过椭圆的中心,且分别交椭圆与直线于不同的三点, ,(点在线段上),直线分别交直线,于点,.
求证:四边形为平行四边形.
22. (12分)
已知函数,其中为实数.
(Ⅰ)若函数是定义域上的单调函数,求的取值范围;
(Ⅱ)若与为方程的两个不等实根,恒成立,求实数的取值范围.
相关试卷
这是一份2024 年沈阳市高中三年级教学质量监测(一)数学试卷及参考答案,文件包含2024年沈阳市高中三年级教学质量监测一数学参考答案pdf、2024年沈阳市高中三年级教学质量监测一数学试卷pdf等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
这是一份2024 年沈阳市高中三年级教学质量监测(一)数学试卷及参考答案,文件包含2024年沈阳市高中三年级教学质量监测一数学试卷pdf、2024年沈阳市高中三年级教学质量监测一数学参考答案pdf等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
这是一份2024 年沈阳市高中三年级教学质量监测(一)数学试题含参考答案,共27页。









