人教B版 (2019)选择性必修 第一册1.1.3 空间向量的坐标与空间直角坐标系习题

这是一份人教B版 (2019)选择性必修 第一册1.1.3 空间向量的坐标与空间直角坐标系习题，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．已知a＝(1，1，0)，b＝(0，1，1)，c＝(1，0，1)，p＝a－b，q＝a＋2b－c，则p·q＝( )
A．－1B．1
C．0D．－2
2．已知a＝(1，5，－2)，b＝(m，2，m＋2)，若a⊥b，则m的值为( )
A．－6B．2
C．6D．8
3．若向量a＝(1，λ，2)，b＝(2，－1，2)，且a与b的夹角的余弦值为，则λ＝( )
A．2B．－2
C．－2或D．2或－
4．已知a＝(－2，－3，1)，b＝(2，0，4)，c＝(－4，－6，2)，则下列结论正确的是( )
A．a∥c，b∥cB．a∥b，a⊥c
C．a∥c，a⊥bD．以上都不对
二、填空题
5．与a＝(2，－1，2)共线且满足a·z＝－18的向量z＝________．
6．已知a＝(2，4，x)，b＝(1，y，2)，
(1)若a∥b，则y＝________；
(2)若|a|＝6，且a⊥b，则y＝________．
7．已知点A(－1，3，1)，B(－1，3，4)，D(1，1，1)，若＝2，则||的值是________．
三、解答题
8．已知点A，B，C的坐标分别(0，1，0)，(－1，0，－1)，(2，1，1)，点P的坐标为(x，0，z)，若PA⊥AB，PA⊥AC，求点P的坐标．
9.棱长为1的正方体ABCD­A1B1C1D1中，E，F，G分别是DD1，BD，BB1的中点．
(1)求证：EF⊥CF；
(2)求与所成角的余弦值；
(3)求||的长．
[尖子生题库]
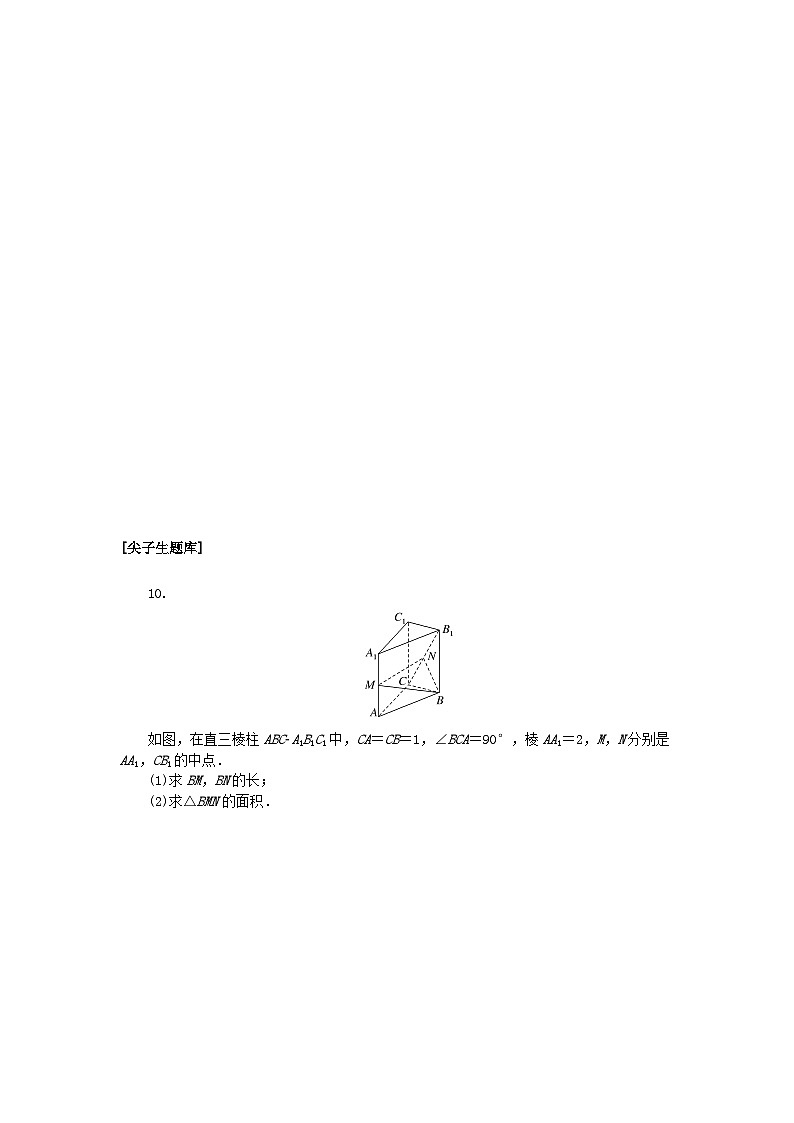
10.
如图，在直三棱柱ABC­A1B1C1中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别是AA1，CB1的中点．
(1)求BM，BN的长；
(2)求△BMN的面积．
课时作业(三) 空间向量的坐标与空间直角坐标系
1．解析：∵p＝a－b＝(1，0，－1)，q＝a＋2b－c＝(0，3，1)，
∴p·q＝1×0＋0×3＋1×(－1)＝－1.
答案：A
2．解析：a⊥b⇒(1，5，－2)·(m，2，m＋2)＝0⇒m＋10－2m－4＝0⇒m＝6.
答案：C
3．解析：由cs〈a，b〉＝＝＝，
解得λ＝－2或λ＝.
答案：C
4．解析：因为c＝(－4，－6，2)＝2a，所以a∥c.又a·b＝0，故a⊥b.
答案：C
5．解析：∵z与a共线，设z＝(2λ，－λ，2λ)．
又a·z＝4λ＋λ＋4λ＝－18，
∴λ＝－2.∴z＝(－4，2，－4)．
答案：(－4，2，－4)
6．解析：(1)由题意得向量a，b的每一个坐标分量均不为零，
所以a∥b⇔＝＝⇔x＝4，y＝2.
(2)依题意得
解得或
答案：(1)2 (2)或－
7．解析：设点P(x，y，z)，则由＝2，
得(x＋1，y－3，z－1)＝2(－1－x，3－y，4－z)，
则
解得即P(－1，3，3)，
则||＝＝＝2.
答案：2
8．解析：由已知得＝(－1，－1，－1)，＝(2，0，1)，＝(－x，1，－z)，由题意得即，解得，∴P(－1，0，2)．
9．解析：
建立如图所示的空间直角坐标系Dxyz，则D(0，0，0)，E(0，0，)，C(0，1，0)，F(，0)，G(1，1，)，
∴＝(，－)，＝(，－，0)，＝(1，0，)，＝(0，－1，)．
(1)证明：∵·＝×(－)＋(－)×0＝0，∴⊥，即EF⊥CF.
(2)∵·＝×1＋×0＋(－)×＝，
||＝＝
||＝＝，
∴cs〈〉＝＝＝.
(3)||＝＝.
10.
解析：以C为原点，以CA，CB，CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系(如图)．
则B(0，1，0)，M(1，0，1)，N.
(1)∵＝(1，－1，1)，
＝
∴||＝＝，
||＝＝.
故BM的长为，BN的长为.
(2)∵cs∠MBN＝cs〈〉＝＝＝，
∴sin∠MBN＝＝，
故S△BMN＝||·||·sin∠MBN＝＝.
即△BMN的面积为.