
还剩32页未读,
继续阅读
成套系列资料,整套一键下载
苏科版数学七年级上册同步专题热点难点练习 专题5.4 走进图形世界(章节复习+能力强化卷)学生版+教师版
展开
这是一份苏科版数学七年级上册同步专题热点难点练习 专题5.4 走进图形世界(章节复习+能力强化卷)学生版+教师版,共35页。
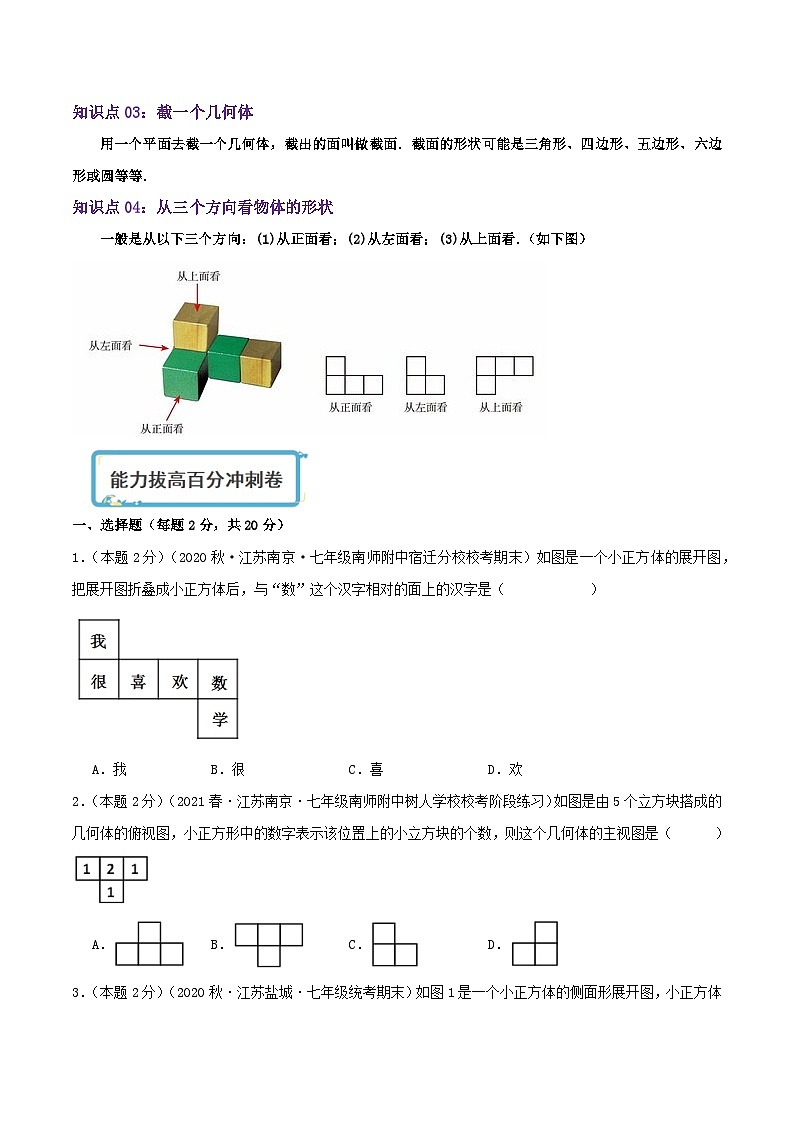
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题5.4 走进图形世界(章节复习+能力强化卷)知识点01:立体图形定义:图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体、圆柱、圆锥、球等.棱柱、棱锥也是常见的立体图形. 知识要点:常见的立体图形有两种分类方法:棱柱的相关概念:在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱. 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……(如下图)知识要点:(1)棱柱所有侧棱长都相等.棱柱的上、下底面的形状相同,侧面的形状都是平行四边形. (2)长方体、正方体都是四棱柱. (3)棱柱可分为直棱柱和斜棱柱.直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形.3.点、线、面、体:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体.知识点02:展开与折叠有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.知识要点:(1)不是所有的立体图形都可以展成平面图形.例如,球便不能展成平面图形.(2)不同的立体图形可展成不同的平面图形;同一个立体图形,沿不同的棱剪开,也可得到不同的平面图.知识点03:截一个几何体用一个平面去截一个几何体,截出的面叫做截面.截面的形状可能是三角形、四边形、五边形、六边形或圆等等.知识点04:从三个方向看物体的形状一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.(如下图)一、选择题(每题2分,共20分)1.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个小正方体的展开图,把展开图折叠成小正方体后,与“数”这个汉字相对的面上的汉字是( )A.我 B.很 C.喜 D.欢2.(本题2分)(2021春·江苏南京·七年级南师附中树人学校校考阶段练习)如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.3.(本题2分)(2020秋·江苏盐城·七年级统考期末)如图1是一个小正方体的侧面形展开图,小正方体从图2中右边所示的位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )A.中 B.国 C.江 D.苏4.(本题2分)(2020秋·江苏南京·七年级统考期末)如图所示,在一个正方形盒子的六面上写有“祝”、“母”、“校”、“更”、“美”、“丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向) 不可能的是( )A. B. C. D.5.(本题2分)(2020秋·江苏徐州·七年级校考阶段练习)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则的值为( )A.-2 B.-3 C.2 D.16.(本题2分)(2019春·江苏无锡·七年级无锡市江南中学校考开学考试)如图是一个正四面体,现沿它的棱AB、AC、AD剪开展成平面图形,则所得的展开图是( )A. B.C. D.7.(本题2分)(2019秋·江苏苏州·七年级统考期末)由个相同的小正方体搭成的几何体,其主视图和俯视图如图所示,则的最小值为( )A.10 B.11 C.12 D.138.(本题2分)(2022秋·江苏宿迁·七年级泗阳致远中学校考期末)在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点。该几何体模型可能是( )A.球 B.三棱锥 C.圆锥 D.圆柱9.(本题2分)(2019秋·江苏连云港·七年级统考阶段练习)下列几何中,属于棱柱的是( )① ② ③ ④ ⑤ ⑥A.①③ B.① C.①③⑥ D.①⑥10.(本题2分)(2019秋·江苏盐城·七年级校联考阶段练习)一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同的方向看形如图所示,则字母D的对面是( ) A.字母A B.字母F C.字母E D.字母B二、填空题(每题2分,共20分)11.(本题2分)(2022秋·江苏无锡·七年级江苏省天一中学校考阶段练习)已知图1的小正方形和图2中所有小正方形都完全一样,将图1的小正方形放在图2中的①、②、③、④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .12.(本题2分)(2022秋·江苏苏州·七年级太仓市第一中学校考阶段练习)一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于5,则a+b+c= .13.(本题2分)(2022秋·七年级单元测试)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有 种.14.(本题2分)(2022秋·江苏·七年级期末)如图,是一个由若干个小正方体搭成的几何体的主视图与视图,设搭这样的几何体最多需要m块小立方块,最少需要n块小立方块,则m+n= .15.(本题2分)(2022秋·江苏·七年级专题练习)一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为 cm3.16.(本题2分)(2022秋·江苏·七年级专题练习)两个同样大小的正方体积木,每个正方体上相对两个面上写的数之和都等于2,现将两个这样的正方体重叠放置(如图),且看得见的五个面上的数如图所示,问看不见的七个面上所写的数之和是 .17.(本题2分)(2021秋·江苏·七年级专题练习)一个长方形的长AB为5cm,宽CD为3cm,则绕某一边旋转一周,得到一个圆柱体,则该圆柱体的体积是 cm3.(保留π)18.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个几何体的展开图,则这个几何体有 条棱.19.(本题2分)(2019秋·江苏苏州·七年级统考期中)如图,墙角处有6个棱长为1分米的正方体纸盒,露在外面的面积之和是 平方分米.20.(本题2分)(2018秋·江苏南通·七年级校考期中)如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是 .三、解答题(共60分)21.(本题6分)(2023秋·江苏镇江·七年级统考期末)一个几何体由大小相同的小立方块搭成,这个几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小方块的个数,请画出这个几何体的主视图和左视图.(为便于观察,把需要的小方格涂上阴影,示例:). 22.(本题6分)(2023秋·江苏镇江·七年级统考期末)如图,在桌面上,有一个由7个完全相同的小正方体搭成的几何体.(1)请画出这个几何体的左视图和俯视图;(2)若现在你的手头还有一些完全相同的小正方体可添放在几何体上,要保持左视图和俯视图不变,则最多可以添加________个小正方体.23.(本题8分)(2022秋·江苏·七年级专题练习)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.(1)若,,则这个无盖长方体盒子的底面面积为______;(2)用含a和h的代数式表示这个无盖长方体盒子的容积______;(3)若,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明:当h是正整数时,这个无盖长方体盒子的最大容积是______.24.(本题8分)(2022秋·七年级单元测试)如图是由棱长都为lcm的6块小正方体组成的简单几何体.(1)请在方格中画出该几何体的三个视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加______块小正方体,(3)直接写出添加最多的小正方体后该几何体的表面积(包含底面).25.(本题8分)(2022秋·七年级单元测试)如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图拼完后,小华看来看去总觉得所拼图形似乎存在问题,(1)请你帮小华分析一下拼图是否存在问题,若有多余块,则把图中多余部分涂黑;若还缺少则直接在原图中补全;(2)若图中的正方形边长为,长方形的长为,宽为,求出修正后所折叠而成的长方体的体积.26.(本题8分)(2022秋·七年级单元测试)如图所示,图1为一个棱长为6的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:(1)如果正方体相对面上的两个数字之和相等,则x=___________,y=___________;(2)如果面“2”是左面,面“4”在后面,则上面是___________(填6或10或x或y);(3)图1中,点M为所在棱的中点,在图2中找到点M的位置,直接写出图2中的面积___________.27.(本题8分)(2018秋·江苏无锡·七年级阶段练习)在桌面上,有6个完全相同的小正方体对成的一个几何体,如图所示.(1)请画出这个几何体的三视图.(2)若将此几何A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有____个.(3)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,则共有______种添法. 请在图2中画出几何体B的俯视图可能的两种不同情形.(4)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添___________个.28.(本题8分)(2022秋·江苏扬州·七年级校考阶段练习)用小立方块搭一个几何体,使它从正面和上面看到的形状如下图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:(1)俯视图中b=__________,a=__________.(2)这个几何体最少由__________个小立方块搭成.(3)能搭出满足条件的几何体共__________种情况,请在所给网格图中画出小立方块最多时几何体的左视图.(为便于观察,请将视图中的小方格用斜线阴影标注,示例:). 2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题5.4 走进图形世界(章节复习+能力强化卷)知识点01:立体图形定义:图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体、圆柱、圆锥、球等.棱柱、棱锥也是常见的立体图形. 知识要点:常见的立体图形有两种分类方法:棱柱的相关概念:在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱. 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……(如下图)知识要点:(1)棱柱所有侧棱长都相等.棱柱的上、下底面的形状相同,侧面的形状都是平行四边形. (2)长方体、正方体都是四棱柱. (3)棱柱可分为直棱柱和斜棱柱.直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形.3.点、线、面、体:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体.知识点02:展开与折叠有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.知识要点:(1)不是所有的立体图形都可以展成平面图形.例如,球便不能展成平面图形.(2)不同的立体图形可展成不同的平面图形;同一个立体图形,沿不同的棱剪开,也可得到不同的平面图.知识点03:截一个几何体用一个平面去截一个几何体,截出的面叫做截面.截面的形状可能是三角形、四边形、五边形、六边形或圆等等.知识点04:从三个方向看物体的形状一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.(如下图)一、选择题(每题2分,共20分)1.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个小正方体的展开图,把展开图折叠成小正方体后,与“数”这个汉字相对的面上的汉字是( )A.我 B.很 C.喜 D.欢【答案】C【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】正方体的表面展开图,与“很”字相对的面上的汉字是“欢”,与“喜”字相对的面上的汉字是“数”,与“学”字相对的面上的汉字是“我”,故选:C.【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.2.(本题2分)(2021春·江苏南京·七年级南师附中树人学校校考阶段练习)如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.【答案】A【分析】先细心观察原立体图形中正方体的位置关系,从正面看去,一共三列,左边有1竖列,有1个立方块;中间有2竖列,其中1列有2个立方块;右边是1竖列,有1个立方块;结合四个选项选出答案.【详解】解:从正面看去,一共三列,左边有1竖列,中间有2竖列,其中1列有2个立方块,右边是1竖列.故选:A.【点睛】本题考查了由三视图判断几何体及简单组合体的三视图,重点考查几何体的三视图及空间想象能力.3.(本题2分)(2020秋·江苏盐城·七年级统考期末)如图1是一个小正方体的侧面形展开图,小正方体从图2中右边所示的位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )A.中 B.国 C.江 D.苏【答案】B【分析】先根据翻转的方向确定底面上的字,再由平面图形的折叠及立体图形的表面展开图的特点得出朝上一面的字即可得答案.【详解】由题意可知正方体翻转到3时,“盐”字在底面,∵正方体表面展开图相对面之间一定相隔一个正方形,∴“盐”字的对面是“国”字,∴小正方体朝上一面的字是“国”,故选:B.【点睛】本题考查正方体相对两个面上的文字,熟练掌握正方体的表面展开图相对面之间一定相隔一个正方形的特点并解结合实际操作是解题关键.4.(本题2分)(2020秋·江苏南京·七年级统考期末)如图所示,在一个正方形盒子的六面上写有“祝”、“母”、“校”、“更”、“美”、“丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向) 不可能的是( )A. B. C. D.【答案】D【分析】根据立方体的平面展开图规律解决问题即可.【详解】由图可得,A,B,C、D选项“祝”与“更”,“母”与“美”都在相对的面上,但D选项中,围成小正方体后,当“祝”与“母”的位置与已知正方形盒子的位置相同时, “校”在左边,不在图上的位置,故这个盒子的展开图不可能是D.故选:D.【点睛】本题主要考查了正方体的展开图,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.5.(本题2分)(2020秋·江苏徐州·七年级校考阶段练习)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则的值为( )A.-2 B.-3 C.2 D.1【答案】C【分析】利用正方体及其表面展开图的特点,根据相对面上的两个数互为相反数,列出方程求出x、y的值,从而得到x+y的值.【详解】这是一个正方体的平面展开图,共有六个面,其中面“1”与面“x”相对,面“-3”与面“y”相对.因为相对面上的两个数互为相反数,所以 解得:则x+y=2故选:C【点睛】本题考查了正方体的平面展开图,注意从相对面入手,分析及解答问题.6.(本题2分)(2019春·江苏无锡·七年级无锡市江南中学校考开学考试)如图是一个正四面体,现沿它的棱AB、AC、AD剪开展成平面图形,则所得的展开图是( )A. B.C. D.【答案】B【分析】亲自动手具体操作,或根据三棱锥的图形特点作答.【详解】沿它的棱AB、AC、AD剪开展开后会以BC、CD、BD向外展开形成如图B样的图形,故选:B.【点睛】本题考查了几何体的展开图的知识,动手具体操作的同时,注意培养空间想象能力.7.(本题2分)(2019秋·江苏苏州·七年级统考期末)由个相同的小正方体搭成的几何体,其主视图和俯视图如图所示,则的最小值为( )A.10 B.11 C.12 D.13【答案】C【分析】根据主视图、俯视图是分别从物体正面和上面看,所得到的图形即可求出答案.【详解】由俯视图知,最少有7个立方块,∵由正视图知在最左边前后两层每层3个立方体,中间3个每层2个立方体和最右边前两排每层3个立方体,∴n的最小值是:7+5=12,故选C.【点睛】此题主要考查了由三视图判断几何体,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.8.(本题2分)(2022秋·江苏宿迁·七年级泗阳致远中学校考期末)在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点。该几何体模型可能是( )A.球 B.三棱锥 C.圆锥 D.圆柱【答案】C【分析】根据每个几何体的特点可得答案.【详解】解:A. 球,只有曲面,不符合题意;B. 三棱锥,面是4个平面,还有4个顶点,不符合题意; C. 圆锥,是一个曲面,一个顶点,符合题意; D. 圆柱,是一个曲面,两个平面,没有顶点,不符合题意.故选:C.【点睛】本题考查认识立体图形,解题关键是熟记常见几何体的特征.9.(本题2分)(2019秋·江苏连云港·七年级统考阶段练习)下列几何中,属于棱柱的是( )① ② ③ ④ ⑤ ⑥A.①③ B.① C.①③⑥ D.①⑥【答案】C【分析】根据棱柱的定义解答即可.【详解】解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.故选:C.【点睛】本题主要考查的是认识立体图形,掌握棱柱的定义是解题的关键.10.(本题2分)(2019秋·江苏盐城·七年级校联考阶段练习)一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同的方向看形如图所示,则字母D的对面是( ) A.字母A B.字母F C.字母E D.字母B【答案】D【分析】根据与A相邻的四个面上的数字确定即可.【详解】由图可知,A相邻的四个面上的字母是B、D、E、F,所以,字母D的对面是字母B.故选:D.【点睛】本题考查了正方体相对两个面上的文字,仔细观察图形从相邻面考虑求解是解题的关键.二、填空题(每题2分,共20分)11.(本题2分)(2022秋·江苏无锡·七年级江苏省天一中学校考阶段练习)已知图1的小正方形和图2中所有小正方形都完全一样,将图1的小正方形放在图2中的①、②、③、④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .【答案】①【分析】根据正方体展开图判断即可.【详解】根据正方体展开图,可知道:②、③、④位置都是可以的,只有①不行,故答案为:①.【点睛】本题考查了正方体的展开图,熟练掌握展开图的方式是解题的关键.12.(本题2分)(2022秋·江苏苏州·七年级太仓市第一中学校考阶段练习)一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于5,则a+b+c= .【答案】11【分析】长方体的表面展开图,相对的面之间一定相隔一个长方形,根据这一特点作答即可.【详解】解:∵长方体的表面展开图,相对的面之间一定相隔一个长方形,∴“-1”与“a”是相对面,“3”与“c”是相对面,“2”与“b”是相对面,又∵相对的两个面上的数字之和等于5,∴a=6,b=3,c=2,∴a+b+c=6+3+2=11,故答案为:11.【点睛】本题主要考查了正方体相对两个面上的文字,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.13.(本题2分)(2022秋·七年级单元测试)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有 种.【答案】3【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.【详解】解:根据正方体的表面展开图可得共有3种,如图:【点睛】此题主要考查了正方体的平面展开图,应灵活掌握,不能死记硬背.14.(本题2分)(2022秋·江苏·七年级期末)如图,是一个由若干个小正方体搭成的几何体的主视图与视图,设搭这样的几何体最多需要m块小立方块,最少需要n块小立方块,则m+n= .【答案】15【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,相加即可.【详解】解:有两种可能;有主视图可得:这个几何体共有3层,由俯视图可得:第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,故:最多m为3+4+1=8个小立方块,最少n为个2+4+1=7小立方块.m+n=15,故答案为:15【点睛】此题主要考查了由三视图判断几何体,关键是掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就很容易得到答案.15.(本题2分)(2022秋·江苏·七年级专题练习)一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为 cm3.【答案】6552【分析】根据题意,从这张纸板上在它的四个角上剪去大小相等的四个正方形,然后做成一个无盖的纸盒.也就是纸板的长和宽分别减去所剪正方形的两个边长,是纸盒的长和宽,纸盒的高就等于所剪去的正方形的边长;当纸盒的长、宽、高三个值最接近时,它们的容积最大;因此可以设减去的正方形的边长为x厘米,列方程解答.【详解】解:设减去的正方形的边长为x厘米,则体积V=x(50-2x)(40-2x)=2×2x(25-x)(20-x);因为2x+(25-x)+(20-x)=45,当2x、(25-x)、(20-x)三个值最接近时,积最大,而每一项=45÷3=15时,积最大,而取整数厘米,所以2x=14,即x=7时;这时纸盒的容积v=(50-7×2)×(40-7×2)×7,=36×26×7,=6552cm3;故答案为:6552【点睛】此题解答关键是理解当折成的纸盒的长、宽、高三个值最接近时,它们的积最大;列方程求出减求的正方形的边长,再根据长方体的体积(容积)公式解答即可.16.(本题2分)(2022秋·江苏·七年级专题练习)两个同样大小的正方体积木,每个正方体上相对两个面上写的数之和都等于2,现将两个这样的正方体重叠放置(如图),且看得见的五个面上的数如图所示,问看不见的七个面上所写的数之和是 .【答案】【分析】先根据“相对两个面上写的数之和都等于2”求出看不见的七个面上的数(或两个相对面上的数之和),再相加即可得.【详解】每个正方体上相对两个面上写的数之和都等于2,左边正方体:下底面上的数是,后面上的数是,左右两相对面上的数之和是2,右边正方体:下底面上的数是,后面上的数是,左面上的数是,则看不见的七个面上所写的数之和是,故答案为:.【点睛】本题考查了正方体相对面上的数、有理数加减法的实际应用,熟练掌握正方体的特征是解题关键.17.(本题2分)(2021秋·江苏·七年级专题练习)一个长方形的长AB为5cm,宽CD为3cm,则绕某一边旋转一周,得到一个圆柱体,则该圆柱体的体积是 cm3.(保留π)【答案】45π或75π【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.【详解】解:分两种情况:①绕长AB所在的直线旋转一周得到圆柱体积为:π×32×5=45π(cm3);②绕宽CD所在的直线旋转一周得到圆柱体积为:π×52×3=75π(cm3).故它们的体积分别为45πcm3或75πcm3.故答案为:45π或75π.【点睛】本题考查了点线面体,利用圆柱的体积公式是解题关键,要分类讨论,以防遗漏.18.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个几何体的展开图,则这个几何体有 条棱.【答案】9【分析】根据侧面为n个长方形,底面为n边形,原几何体为n棱柱,依此即可求解.【详解】解:因为侧面为3个长方形,底面为三角形,故原几何体为3棱柱,故这个几何体有9条棱;故答案为:9.【点睛】本题考查了几何体的展开图,n棱柱的展开图侧面为n个长方形,底面为n边形.19.(本题2分)(2019秋·江苏苏州·七年级统考期中)如图,墙角处有6个棱长为1分米的正方体纸盒,露在外面的面积之和是 平方分米.【答案】12【分析】观察图形知道,露在外面的面:上面一层是3个,下面一层是9个,所以一共是3+9=12个,由此根据正方形的面积公式S=a×a,求出一个正方形的面积,再乘12即可.【详解】解:1×1×(3+9)=1×12=12(平方分米);∴露在外面的面积是:12平方分米.故答案为12.【点睛】本题考查了求表面积,此题关键是正确数出露在外面的面有几个,再根据正方形的面积公式解决问题.20.(本题2分)(2018秋·江苏南通·七年级校考期中)如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是 .【答案】54a2【分析】求这个几何体的表面积,就要数出这个几何体中小正方体漏在外面的面的个数,从前、后、左、右、上、下方向上来数,然后用一个面的面积乘面的个数即可.【详解】解:从前、后、左、右、上、下方向看到的面数分别为:10,10,8,8,9,9所以表面积为(10+10+8+8+9+9 )a2=54a2,故答案为54a2.【点睛】本题主要考查组合体的表面积,分析图形,掌握表面积的计算公式是解题的关键.三、解答题(共60分)21.(本题6分)(2023秋·江苏镇江·七年级统考期末)一个几何体由大小相同的小立方块搭成,这个几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小方块的个数,请画出这个几何体的主视图和左视图.(为便于观察,把需要的小方格涂上阴影,示例:). 【答案】见解析【分析】主视图有3列,每列小正方形数目分别为3,4,2,左视图有2列,每列小正方数形数目分别为4,2,据此可画出图形.【详解】解:如图所示: .【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.22.(本题6分)(2023秋·江苏镇江·七年级统考期末)如图,在桌面上,有一个由7个完全相同的小正方体搭成的几何体.(1)请画出这个几何体的左视图和俯视图;(2)若现在你的手头还有一些完全相同的小正方体可添放在几何体上,要保持左视图和俯视图不变,则最多可以添加________个小正方体.【答案】(1)见解析;(2)3.【分析】(1)根据三视图的画法,画出图形即可求解;(2)从俯视图的角度出发,同时考虑左视图的情况,即可求解.【详解】(1)如图所示:(2)如图所示:保持左视图和俯视图不变,则最多可以添加3个小正方体.【点睛】本题考查三视图的画法,解题的关键是掌握画三视图的方法.23.(本题8分)(2022秋·江苏·七年级专题练习)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.(1)若,,则这个无盖长方体盒子的底面面积为______;(2)用含a和h的代数式表示这个无盖长方体盒子的容积______;(3)若,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明:当h是正整数时,这个无盖长方体盒子的最大容积是______.【答案】(1)(2)(3)【分析】(1)根据已知得出长方体底面的边长进而求出即可;(2)由于原来正方形的边长为a,如果四个角上各剪去一个同样大小的正方形,那么无盖长方体的底面的长宽分别都是,高是h,由此即可表示这个无盖长方体的容积;(3)根据材料一定,长方体中体积最大与底面各积和高都有关进行解答即可.【详解】(1)∵,,∴这个无盖长方体盒子的底面面积为:,故答案为;(2)这个无盖长方体盒子的容积,故答案为;(3)若,当h越大,无盖长方体盒子的容积V不一定就越大,如时,体积,时,体积;∵,∴当时,体积最大,即时,此时体积最大,∴这个无盖长方体盒子的最大容积是:,故答案为.【点睛】本题考查了几何体的体积求法以及展开图面积问题,根据题意表示出长方体体积是解题关键.24.(本题8分)(2022秋·七年级单元测试)如图是由棱长都为lcm的6块小正方体组成的简单几何体.(1)请在方格中画出该几何体的三个视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加______块小正方体,(3)直接写出添加最多的小正方体后该几何体的表面积(包含底面).【答案】(1)见解析(2)2(3)【分析】(1)根据三视图的定义画出图形即可;(2)根据题目条件解决问题即可;(3)求出各个面上的小正方形个数,即可得出答案.【详解】(1)解:该几何体的主视图、左视图和俯视图如下:(2)解:在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加2个小正方体,故答案为:2.(3)解:,答:添加最多的小正方体后该几何体的表面积为.【点睛】本题考查作图-三视图,熟练掌握基本知识,正确掌握不同视图的观察角度是解题关键.25.(本题8分)(2022秋·七年级单元测试)如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图拼完后,小华看来看去总觉得所拼图形似乎存在问题,(1)请你帮小华分析一下拼图是否存在问题,若有多余块,则把图中多余部分涂黑;若还缺少则直接在原图中补全;(2)若图中的正方形边长为,长方形的长为,宽为,求出修正后所折叠而成的长方体的体积.【答案】(1)有多余块,图见解析(2)【分析】(1)长方体有6个面,依据长方体的特征进行判断即可;(2)依据长方体的棱长,运用公式即可得到表面积以及体积.【详解】(1)解:根据长方体有6个面,可得拼图中有多余块,多余部分如图所示:(2)解:体积=.【点睛】本题考查了展开图折叠成几何题,利用长方体展开图中每个面都有一个全等的对面是解题关键.26.(本题8分)(2022秋·七年级单元测试)如图所示,图1为一个棱长为6的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:(1)如果正方体相对面上的两个数字之和相等,则x=___________,y=___________;(2)如果面“2”是左面,面“4”在后面,则上面是___________(填6或10或x或y);(3)图1中,点M为所在棱的中点,在图2中找到点M的位置,直接写出图2中的面积___________.【答案】(1)12,8(2)y(3)9或45【分析】(1)根据两个面相隔一个面是对面,对面的和是14,列式可得答案;(2)根据临面,对面的关系,可得答案;(3)根据展开图面与面的关系,可得M的位置,根据三角形的面积公式,可得答案.【详解】(1)解:如果长方体相对面上的两个数字之和相等,则x+2=y+6=10+4,解得:x=12,y=8;故答案为:12,8;(2)解:如果面“2”是左面,面“4”在后面,则上面是y.故答案为:y;(3)解:如图:,或,故的面积为9或45,故答案为:9或45.【点睛】本题主要考查了正方体展开图面与面之间的关系,熟悉并熟练掌握展开图面与面之间的关系是解决问题的关键.27.(本题8分)(2018秋·江苏无锡·七年级阶段练习)在桌面上,有6个完全相同的小正方体对成的一个几何体,如图所示.(1)请画出这个几何体的三视图.(2)若将此几何A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有____个.(3)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,则共有______种添法. 请在图2中画出几何体B的俯视图可能的两种不同情形.(4)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添___________个.【答案】(1)详见解析;(2)2个;(3)4种;(4)4个.【分析】见详解.【详解】(1)如下图(2)三个面是红色的有2个,为从上往下数第二行第一列的那两个.(3)4种添发;见下图,答案不唯一.(4)由图可知该几何体最多有10个正方体,几何体A只有6个小正方体,10-6=4,所以最多可以添加4个正方体.【点睛】本题考查了物体的三视图,中等难度,培养看图能力、空间感是解题关键.28.(本题8分)(2022秋·江苏扬州·七年级校考阶段练习)用小立方块搭一个几何体,使它从正面和上面看到的形状如下图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:(1)俯视图中b=__________,a=__________.(2)这个几何体最少由__________个小立方块搭成.(3)能搭出满足条件的几何体共__________种情况,请在所给网格图中画出小立方块最多时几何体的左视图.(为便于观察,请将视图中的小方格用斜线阴影标注,示例:).【答案】(1)1;3(2)9(3)7【详解】试题分析:(1)由主视图可知,第2列小正方体个数都为1,所以b=1,,第三列小正方体个数为3,所以a=3;(2)正方体个数最少时,第一列正方体个数为:1+1+2=4个,第2列正方体个数为:1+1=2个,第3列正方体个数为:3个,一共有:4+2+3=9个;(3)第2列正方体个数确定为:1+1=2个,第3列正方体个数确定为:3个,第1列正方体情况可能为:①d=1,e=1,f=2;②d=1,e=2,f=1;③d=2,e=1,f=1;④d=2,e=2,f=1;⑤d=2,e=1,f=2;⑥d=1,e=2,f=2;⑦d=2,e=2,f=2,共7种情况,当d=2,e=2,f=2时小立方块最多,左视图如图所示.试题解析:(1)b=1,a=3;(2)1+1+2+1+1+3=9个;(3)共7种情况,当d=2,e=2,f=2时小立方块最多.此时,左视图为:点睛:掌握三视图的画法,并会根据三视图判断对应的正方体的个数.
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题5.4 走进图形世界(章节复习+能力强化卷)知识点01:立体图形定义:图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体、圆柱、圆锥、球等.棱柱、棱锥也是常见的立体图形. 知识要点:常见的立体图形有两种分类方法:棱柱的相关概念:在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱. 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……(如下图)知识要点:(1)棱柱所有侧棱长都相等.棱柱的上、下底面的形状相同,侧面的形状都是平行四边形. (2)长方体、正方体都是四棱柱. (3)棱柱可分为直棱柱和斜棱柱.直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形.3.点、线、面、体:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体.知识点02:展开与折叠有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.知识要点:(1)不是所有的立体图形都可以展成平面图形.例如,球便不能展成平面图形.(2)不同的立体图形可展成不同的平面图形;同一个立体图形,沿不同的棱剪开,也可得到不同的平面图.知识点03:截一个几何体用一个平面去截一个几何体,截出的面叫做截面.截面的形状可能是三角形、四边形、五边形、六边形或圆等等.知识点04:从三个方向看物体的形状一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.(如下图)一、选择题(每题2分,共20分)1.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个小正方体的展开图,把展开图折叠成小正方体后,与“数”这个汉字相对的面上的汉字是( )A.我 B.很 C.喜 D.欢2.(本题2分)(2021春·江苏南京·七年级南师附中树人学校校考阶段练习)如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.3.(本题2分)(2020秋·江苏盐城·七年级统考期末)如图1是一个小正方体的侧面形展开图,小正方体从图2中右边所示的位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )A.中 B.国 C.江 D.苏4.(本题2分)(2020秋·江苏南京·七年级统考期末)如图所示,在一个正方形盒子的六面上写有“祝”、“母”、“校”、“更”、“美”、“丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向) 不可能的是( )A. B. C. D.5.(本题2分)(2020秋·江苏徐州·七年级校考阶段练习)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则的值为( )A.-2 B.-3 C.2 D.16.(本题2分)(2019春·江苏无锡·七年级无锡市江南中学校考开学考试)如图是一个正四面体,现沿它的棱AB、AC、AD剪开展成平面图形,则所得的展开图是( )A. B.C. D.7.(本题2分)(2019秋·江苏苏州·七年级统考期末)由个相同的小正方体搭成的几何体,其主视图和俯视图如图所示,则的最小值为( )A.10 B.11 C.12 D.138.(本题2分)(2022秋·江苏宿迁·七年级泗阳致远中学校考期末)在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点。该几何体模型可能是( )A.球 B.三棱锥 C.圆锥 D.圆柱9.(本题2分)(2019秋·江苏连云港·七年级统考阶段练习)下列几何中,属于棱柱的是( )① ② ③ ④ ⑤ ⑥A.①③ B.① C.①③⑥ D.①⑥10.(本题2分)(2019秋·江苏盐城·七年级校联考阶段练习)一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同的方向看形如图所示,则字母D的对面是( ) A.字母A B.字母F C.字母E D.字母B二、填空题(每题2分,共20分)11.(本题2分)(2022秋·江苏无锡·七年级江苏省天一中学校考阶段练习)已知图1的小正方形和图2中所有小正方形都完全一样,将图1的小正方形放在图2中的①、②、③、④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .12.(本题2分)(2022秋·江苏苏州·七年级太仓市第一中学校考阶段练习)一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于5,则a+b+c= .13.(本题2分)(2022秋·七年级单元测试)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有 种.14.(本题2分)(2022秋·江苏·七年级期末)如图,是一个由若干个小正方体搭成的几何体的主视图与视图,设搭这样的几何体最多需要m块小立方块,最少需要n块小立方块,则m+n= .15.(本题2分)(2022秋·江苏·七年级专题练习)一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为 cm3.16.(本题2分)(2022秋·江苏·七年级专题练习)两个同样大小的正方体积木,每个正方体上相对两个面上写的数之和都等于2,现将两个这样的正方体重叠放置(如图),且看得见的五个面上的数如图所示,问看不见的七个面上所写的数之和是 .17.(本题2分)(2021秋·江苏·七年级专题练习)一个长方形的长AB为5cm,宽CD为3cm,则绕某一边旋转一周,得到一个圆柱体,则该圆柱体的体积是 cm3.(保留π)18.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个几何体的展开图,则这个几何体有 条棱.19.(本题2分)(2019秋·江苏苏州·七年级统考期中)如图,墙角处有6个棱长为1分米的正方体纸盒,露在外面的面积之和是 平方分米.20.(本题2分)(2018秋·江苏南通·七年级校考期中)如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是 .三、解答题(共60分)21.(本题6分)(2023秋·江苏镇江·七年级统考期末)一个几何体由大小相同的小立方块搭成,这个几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小方块的个数,请画出这个几何体的主视图和左视图.(为便于观察,把需要的小方格涂上阴影,示例:). 22.(本题6分)(2023秋·江苏镇江·七年级统考期末)如图,在桌面上,有一个由7个完全相同的小正方体搭成的几何体.(1)请画出这个几何体的左视图和俯视图;(2)若现在你的手头还有一些完全相同的小正方体可添放在几何体上,要保持左视图和俯视图不变,则最多可以添加________个小正方体.23.(本题8分)(2022秋·江苏·七年级专题练习)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.(1)若,,则这个无盖长方体盒子的底面面积为______;(2)用含a和h的代数式表示这个无盖长方体盒子的容积______;(3)若,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明:当h是正整数时,这个无盖长方体盒子的最大容积是______.24.(本题8分)(2022秋·七年级单元测试)如图是由棱长都为lcm的6块小正方体组成的简单几何体.(1)请在方格中画出该几何体的三个视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加______块小正方体,(3)直接写出添加最多的小正方体后该几何体的表面积(包含底面).25.(本题8分)(2022秋·七年级单元测试)如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图拼完后,小华看来看去总觉得所拼图形似乎存在问题,(1)请你帮小华分析一下拼图是否存在问题,若有多余块,则把图中多余部分涂黑;若还缺少则直接在原图中补全;(2)若图中的正方形边长为,长方形的长为,宽为,求出修正后所折叠而成的长方体的体积.26.(本题8分)(2022秋·七年级单元测试)如图所示,图1为一个棱长为6的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:(1)如果正方体相对面上的两个数字之和相等,则x=___________,y=___________;(2)如果面“2”是左面,面“4”在后面,则上面是___________(填6或10或x或y);(3)图1中,点M为所在棱的中点,在图2中找到点M的位置,直接写出图2中的面积___________.27.(本题8分)(2018秋·江苏无锡·七年级阶段练习)在桌面上,有6个完全相同的小正方体对成的一个几何体,如图所示.(1)请画出这个几何体的三视图.(2)若将此几何A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有____个.(3)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,则共有______种添法. 请在图2中画出几何体B的俯视图可能的两种不同情形.(4)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添___________个.28.(本题8分)(2022秋·江苏扬州·七年级校考阶段练习)用小立方块搭一个几何体,使它从正面和上面看到的形状如下图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:(1)俯视图中b=__________,a=__________.(2)这个几何体最少由__________个小立方块搭成.(3)能搭出满足条件的几何体共__________种情况,请在所给网格图中画出小立方块最多时几何体的左视图.(为便于观察,请将视图中的小方格用斜线阴影标注,示例:). 2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习专题5.4 走进图形世界(章节复习+能力强化卷)知识点01:立体图形定义:图形的各部分不都在同一平面内,这样的图形就是立体图形,如长方体、圆柱、圆锥、球等.棱柱、棱锥也是常见的立体图形. 知识要点:常见的立体图形有两种分类方法:棱柱的相关概念:在棱柱中,相邻两个面的交线叫做棱,相邻两个侧面的交线叫做侧棱. 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……(如下图)知识要点:(1)棱柱所有侧棱长都相等.棱柱的上、下底面的形状相同,侧面的形状都是平行四边形. (2)长方体、正方体都是四棱柱. (3)棱柱可分为直棱柱和斜棱柱.直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形.3.点、线、面、体:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体;包围着体的是面,面有平的面和曲的面两种;面和面相交的地方形成线,线也分为直线和曲线两种;线和线相交的地方形成点.从上面的描述中我们可以看出点、线、面、体之间的关系. 此外,从运动的观点看:点动成线,线动成面,面动成体.知识点02:展开与折叠有些立体图形是由一些平面图形围成,将它们的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图.知识要点:(1)不是所有的立体图形都可以展成平面图形.例如,球便不能展成平面图形.(2)不同的立体图形可展成不同的平面图形;同一个立体图形,沿不同的棱剪开,也可得到不同的平面图.知识点03:截一个几何体用一个平面去截一个几何体,截出的面叫做截面.截面的形状可能是三角形、四边形、五边形、六边形或圆等等.知识点04:从三个方向看物体的形状一般是从以下三个方向:(1)从正面看;(2)从左面看;(3)从上面看.(如下图)一、选择题(每题2分,共20分)1.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个小正方体的展开图,把展开图折叠成小正方体后,与“数”这个汉字相对的面上的汉字是( )A.我 B.很 C.喜 D.欢【答案】C【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】正方体的表面展开图,与“很”字相对的面上的汉字是“欢”,与“喜”字相对的面上的汉字是“数”,与“学”字相对的面上的汉字是“我”,故选:C.【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.2.(本题2分)(2021春·江苏南京·七年级南师附中树人学校校考阶段练习)如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )A. B. C. D.【答案】A【分析】先细心观察原立体图形中正方体的位置关系,从正面看去,一共三列,左边有1竖列,有1个立方块;中间有2竖列,其中1列有2个立方块;右边是1竖列,有1个立方块;结合四个选项选出答案.【详解】解:从正面看去,一共三列,左边有1竖列,中间有2竖列,其中1列有2个立方块,右边是1竖列.故选:A.【点睛】本题考查了由三视图判断几何体及简单组合体的三视图,重点考查几何体的三视图及空间想象能力.3.(本题2分)(2020秋·江苏盐城·七年级统考期末)如图1是一个小正方体的侧面形展开图,小正方体从图2中右边所示的位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )A.中 B.国 C.江 D.苏【答案】B【分析】先根据翻转的方向确定底面上的字,再由平面图形的折叠及立体图形的表面展开图的特点得出朝上一面的字即可得答案.【详解】由题意可知正方体翻转到3时,“盐”字在底面,∵正方体表面展开图相对面之间一定相隔一个正方形,∴“盐”字的对面是“国”字,∴小正方体朝上一面的字是“国”,故选:B.【点睛】本题考查正方体相对两个面上的文字,熟练掌握正方体的表面展开图相对面之间一定相隔一个正方形的特点并解结合实际操作是解题关键.4.(本题2分)(2020秋·江苏南京·七年级统考期末)如图所示,在一个正方形盒子的六面上写有“祝”、“母”、“校”、“更”、“美”、“丽”六个汉字,其中“祝”与“更”,“母”与“美”在相对的面上,则这个盒子的展开图(不考虑文字方向) 不可能的是( )A. B. C. D.【答案】D【分析】根据立方体的平面展开图规律解决问题即可.【详解】由图可得,A,B,C、D选项“祝”与“更”,“母”与“美”都在相对的面上,但D选项中,围成小正方体后,当“祝”与“母”的位置与已知正方形盒子的位置相同时, “校”在左边,不在图上的位置,故这个盒子的展开图不可能是D.故选:D.【点睛】本题主要考查了正方体的展开图,对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.5.(本题2分)(2020秋·江苏徐州·七年级校考阶段练习)如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则的值为( )A.-2 B.-3 C.2 D.1【答案】C【分析】利用正方体及其表面展开图的特点,根据相对面上的两个数互为相反数,列出方程求出x、y的值,从而得到x+y的值.【详解】这是一个正方体的平面展开图,共有六个面,其中面“1”与面“x”相对,面“-3”与面“y”相对.因为相对面上的两个数互为相反数,所以 解得:则x+y=2故选:C【点睛】本题考查了正方体的平面展开图,注意从相对面入手,分析及解答问题.6.(本题2分)(2019春·江苏无锡·七年级无锡市江南中学校考开学考试)如图是一个正四面体,现沿它的棱AB、AC、AD剪开展成平面图形,则所得的展开图是( )A. B.C. D.【答案】B【分析】亲自动手具体操作,或根据三棱锥的图形特点作答.【详解】沿它的棱AB、AC、AD剪开展开后会以BC、CD、BD向外展开形成如图B样的图形,故选:B.【点睛】本题考查了几何体的展开图的知识,动手具体操作的同时,注意培养空间想象能力.7.(本题2分)(2019秋·江苏苏州·七年级统考期末)由个相同的小正方体搭成的几何体,其主视图和俯视图如图所示,则的最小值为( )A.10 B.11 C.12 D.13【答案】C【分析】根据主视图、俯视图是分别从物体正面和上面看,所得到的图形即可求出答案.【详解】由俯视图知,最少有7个立方块,∵由正视图知在最左边前后两层每层3个立方体,中间3个每层2个立方体和最右边前两排每层3个立方体,∴n的最小值是:7+5=12,故选C.【点睛】此题主要考查了由三视图判断几何体,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.8.(本题2分)(2022秋·江苏宿迁·七年级泗阳致远中学校考期末)在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点。该几何体模型可能是( )A.球 B.三棱锥 C.圆锥 D.圆柱【答案】C【分析】根据每个几何体的特点可得答案.【详解】解:A. 球,只有曲面,不符合题意;B. 三棱锥,面是4个平面,还有4个顶点,不符合题意; C. 圆锥,是一个曲面,一个顶点,符合题意; D. 圆柱,是一个曲面,两个平面,没有顶点,不符合题意.故选:C.【点睛】本题考查认识立体图形,解题关键是熟记常见几何体的特征.9.(本题2分)(2019秋·江苏连云港·七年级统考阶段练习)下列几何中,属于棱柱的是( )① ② ③ ④ ⑤ ⑥A.①③ B.① C.①③⑥ D.①⑥【答案】C【分析】根据棱柱的定义解答即可.【详解】解:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱.故选:C.【点睛】本题主要考查的是认识立体图形,掌握棱柱的定义是解题的关键.10.(本题2分)(2019秋·江苏盐城·七年级校联考阶段练习)一个小立方块的六个面分别标有字母A,B,C,D,E,F,从三个不同的方向看形如图所示,则字母D的对面是( ) A.字母A B.字母F C.字母E D.字母B【答案】D【分析】根据与A相邻的四个面上的数字确定即可.【详解】由图可知,A相邻的四个面上的字母是B、D、E、F,所以,字母D的对面是字母B.故选:D.【点睛】本题考查了正方体相对两个面上的文字,仔细观察图形从相邻面考虑求解是解题的关键.二、填空题(每题2分,共20分)11.(本题2分)(2022秋·江苏无锡·七年级江苏省天一中学校考阶段练习)已知图1的小正方形和图2中所有小正方形都完全一样,将图1的小正方形放在图2中的①、②、③、④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .【答案】①【分析】根据正方体展开图判断即可.【详解】根据正方体展开图,可知道:②、③、④位置都是可以的,只有①不行,故答案为:①.【点睛】本题考查了正方体的展开图,熟练掌握展开图的方式是解题的关键.12.(本题2分)(2022秋·江苏苏州·七年级太仓市第一中学校考阶段练习)一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于5,则a+b+c= .【答案】11【分析】长方体的表面展开图,相对的面之间一定相隔一个长方形,根据这一特点作答即可.【详解】解:∵长方体的表面展开图,相对的面之间一定相隔一个长方形,∴“-1”与“a”是相对面,“3”与“c”是相对面,“2”与“b”是相对面,又∵相对的两个面上的数字之和等于5,∴a=6,b=3,c=2,∴a+b+c=6+3+2=11,故答案为:11.【点睛】本题主要考查了正方体相对两个面上的文字,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.13.(本题2分)(2022秋·七年级单元测试)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有 种.【答案】3【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.【详解】解:根据正方体的表面展开图可得共有3种,如图:【点睛】此题主要考查了正方体的平面展开图,应灵活掌握,不能死记硬背.14.(本题2分)(2022秋·江苏·七年级期末)如图,是一个由若干个小正方体搭成的几何体的主视图与视图,设搭这样的几何体最多需要m块小立方块,最少需要n块小立方块,则m+n= .【答案】15【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,相加即可.【详解】解:有两种可能;有主视图可得:这个几何体共有3层,由俯视图可得:第一层正方体的个数为4,由主视图可得第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,故:最多m为3+4+1=8个小立方块,最少n为个2+4+1=7小立方块.m+n=15,故答案为:15【点睛】此题主要考查了由三视图判断几何体,关键是掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就很容易得到答案.15.(本题2分)(2022秋·江苏·七年级专题练习)一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为 cm3.【答案】6552【分析】根据题意,从这张纸板上在它的四个角上剪去大小相等的四个正方形,然后做成一个无盖的纸盒.也就是纸板的长和宽分别减去所剪正方形的两个边长,是纸盒的长和宽,纸盒的高就等于所剪去的正方形的边长;当纸盒的长、宽、高三个值最接近时,它们的容积最大;因此可以设减去的正方形的边长为x厘米,列方程解答.【详解】解:设减去的正方形的边长为x厘米,则体积V=x(50-2x)(40-2x)=2×2x(25-x)(20-x);因为2x+(25-x)+(20-x)=45,当2x、(25-x)、(20-x)三个值最接近时,积最大,而每一项=45÷3=15时,积最大,而取整数厘米,所以2x=14,即x=7时;这时纸盒的容积v=(50-7×2)×(40-7×2)×7,=36×26×7,=6552cm3;故答案为:6552【点睛】此题解答关键是理解当折成的纸盒的长、宽、高三个值最接近时,它们的积最大;列方程求出减求的正方形的边长,再根据长方体的体积(容积)公式解答即可.16.(本题2分)(2022秋·江苏·七年级专题练习)两个同样大小的正方体积木,每个正方体上相对两个面上写的数之和都等于2,现将两个这样的正方体重叠放置(如图),且看得见的五个面上的数如图所示,问看不见的七个面上所写的数之和是 .【答案】【分析】先根据“相对两个面上写的数之和都等于2”求出看不见的七个面上的数(或两个相对面上的数之和),再相加即可得.【详解】每个正方体上相对两个面上写的数之和都等于2,左边正方体:下底面上的数是,后面上的数是,左右两相对面上的数之和是2,右边正方体:下底面上的数是,后面上的数是,左面上的数是,则看不见的七个面上所写的数之和是,故答案为:.【点睛】本题考查了正方体相对面上的数、有理数加减法的实际应用,熟练掌握正方体的特征是解题关键.17.(本题2分)(2021秋·江苏·七年级专题练习)一个长方形的长AB为5cm,宽CD为3cm,则绕某一边旋转一周,得到一个圆柱体,则该圆柱体的体积是 cm3.(保留π)【答案】45π或75π【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.【详解】解:分两种情况:①绕长AB所在的直线旋转一周得到圆柱体积为:π×32×5=45π(cm3);②绕宽CD所在的直线旋转一周得到圆柱体积为:π×52×3=75π(cm3).故它们的体积分别为45πcm3或75πcm3.故答案为:45π或75π.【点睛】本题考查了点线面体,利用圆柱的体积公式是解题关键,要分类讨论,以防遗漏.18.(本题2分)(2020秋·江苏南京·七年级南师附中宿迁分校校考期末)如图是一个几何体的展开图,则这个几何体有 条棱.【答案】9【分析】根据侧面为n个长方形,底面为n边形,原几何体为n棱柱,依此即可求解.【详解】解:因为侧面为3个长方形,底面为三角形,故原几何体为3棱柱,故这个几何体有9条棱;故答案为:9.【点睛】本题考查了几何体的展开图,n棱柱的展开图侧面为n个长方形,底面为n边形.19.(本题2分)(2019秋·江苏苏州·七年级统考期中)如图,墙角处有6个棱长为1分米的正方体纸盒,露在外面的面积之和是 平方分米.【答案】12【分析】观察图形知道,露在外面的面:上面一层是3个,下面一层是9个,所以一共是3+9=12个,由此根据正方形的面积公式S=a×a,求出一个正方形的面积,再乘12即可.【详解】解:1×1×(3+9)=1×12=12(平方分米);∴露在外面的面积是:12平方分米.故答案为12.【点睛】本题考查了求表面积,此题关键是正确数出露在外面的面有几个,再根据正方形的面积公式解决问题.20.(本题2分)(2018秋·江苏南通·七年级校考期中)如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是 .【答案】54a2【分析】求这个几何体的表面积,就要数出这个几何体中小正方体漏在外面的面的个数,从前、后、左、右、上、下方向上来数,然后用一个面的面积乘面的个数即可.【详解】解:从前、后、左、右、上、下方向看到的面数分别为:10,10,8,8,9,9所以表面积为(10+10+8+8+9+9 )a2=54a2,故答案为54a2.【点睛】本题主要考查组合体的表面积,分析图形,掌握表面积的计算公式是解题的关键.三、解答题(共60分)21.(本题6分)(2023秋·江苏镇江·七年级统考期末)一个几何体由大小相同的小立方块搭成,这个几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小方块的个数,请画出这个几何体的主视图和左视图.(为便于观察,把需要的小方格涂上阴影,示例:). 【答案】见解析【分析】主视图有3列,每列小正方形数目分别为3,4,2,左视图有2列,每列小正方数形数目分别为4,2,据此可画出图形.【详解】解:如图所示: .【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.22.(本题6分)(2023秋·江苏镇江·七年级统考期末)如图,在桌面上,有一个由7个完全相同的小正方体搭成的几何体.(1)请画出这个几何体的左视图和俯视图;(2)若现在你的手头还有一些完全相同的小正方体可添放在几何体上,要保持左视图和俯视图不变,则最多可以添加________个小正方体.【答案】(1)见解析;(2)3.【分析】(1)根据三视图的画法,画出图形即可求解;(2)从俯视图的角度出发,同时考虑左视图的情况,即可求解.【详解】(1)如图所示:(2)如图所示:保持左视图和俯视图不变,则最多可以添加3个小正方体.【点睛】本题考查三视图的画法,解题的关键是掌握画三视图的方法.23.(本题8分)(2022秋·江苏·七年级专题练习)如图,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.(1)若,,则这个无盖长方体盒子的底面面积为______;(2)用含a和h的代数式表示这个无盖长方体盒子的容积______;(3)若,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明:当h是正整数时,这个无盖长方体盒子的最大容积是______.【答案】(1)(2)(3)【分析】(1)根据已知得出长方体底面的边长进而求出即可;(2)由于原来正方形的边长为a,如果四个角上各剪去一个同样大小的正方形,那么无盖长方体的底面的长宽分别都是,高是h,由此即可表示这个无盖长方体的容积;(3)根据材料一定,长方体中体积最大与底面各积和高都有关进行解答即可.【详解】(1)∵,,∴这个无盖长方体盒子的底面面积为:,故答案为;(2)这个无盖长方体盒子的容积,故答案为;(3)若,当h越大,无盖长方体盒子的容积V不一定就越大,如时,体积,时,体积;∵,∴当时,体积最大,即时,此时体积最大,∴这个无盖长方体盒子的最大容积是:,故答案为.【点睛】本题考查了几何体的体积求法以及展开图面积问题,根据题意表示出长方体体积是解题关键.24.(本题8分)(2022秋·七年级单元测试)如图是由棱长都为lcm的6块小正方体组成的简单几何体.(1)请在方格中画出该几何体的三个视图.(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加______块小正方体,(3)直接写出添加最多的小正方体后该几何体的表面积(包含底面).【答案】(1)见解析(2)2(3)【分析】(1)根据三视图的定义画出图形即可;(2)根据题目条件解决问题即可;(3)求出各个面上的小正方形个数,即可得出答案.【详解】(1)解:该几何体的主视图、左视图和俯视图如下:(2)解:在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加2个小正方体,故答案为:2.(3)解:,答:添加最多的小正方体后该几何体的表面积为.【点睛】本题考查作图-三视图,熟练掌握基本知识,正确掌握不同视图的观察角度是解题关键.25.(本题8分)(2022秋·七年级单元测试)如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图拼完后,小华看来看去总觉得所拼图形似乎存在问题,(1)请你帮小华分析一下拼图是否存在问题,若有多余块,则把图中多余部分涂黑;若还缺少则直接在原图中补全;(2)若图中的正方形边长为,长方形的长为,宽为,求出修正后所折叠而成的长方体的体积.【答案】(1)有多余块,图见解析(2)【分析】(1)长方体有6个面,依据长方体的特征进行判断即可;(2)依据长方体的棱长,运用公式即可得到表面积以及体积.【详解】(1)解:根据长方体有6个面,可得拼图中有多余块,多余部分如图所示:(2)解:体积=.【点睛】本题考查了展开图折叠成几何题,利用长方体展开图中每个面都有一个全等的对面是解题关键.26.(本题8分)(2022秋·七年级单元测试)如图所示,图1为一个棱长为6的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:(1)如果正方体相对面上的两个数字之和相等,则x=___________,y=___________;(2)如果面“2”是左面,面“4”在后面,则上面是___________(填6或10或x或y);(3)图1中,点M为所在棱的中点,在图2中找到点M的位置,直接写出图2中的面积___________.【答案】(1)12,8(2)y(3)9或45【分析】(1)根据两个面相隔一个面是对面,对面的和是14,列式可得答案;(2)根据临面,对面的关系,可得答案;(3)根据展开图面与面的关系,可得M的位置,根据三角形的面积公式,可得答案.【详解】(1)解:如果长方体相对面上的两个数字之和相等,则x+2=y+6=10+4,解得:x=12,y=8;故答案为:12,8;(2)解:如果面“2”是左面,面“4”在后面,则上面是y.故答案为:y;(3)解:如图:,或,故的面积为9或45,故答案为:9或45.【点睛】本题主要考查了正方体展开图面与面之间的关系,熟悉并熟练掌握展开图面与面之间的关系是解决问题的关键.27.(本题8分)(2018秋·江苏无锡·七年级阶段练习)在桌面上,有6个完全相同的小正方体对成的一个几何体,如图所示.(1)请画出这个几何体的三视图.(2)若将此几何A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有____个.(3)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,则共有______种添法. 请在图2中画出几何体B的俯视图可能的两种不同情形.(4)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添___________个.【答案】(1)详见解析;(2)2个;(3)4种;(4)4个.【分析】见详解.【详解】(1)如下图(2)三个面是红色的有2个,为从上往下数第二行第一列的那两个.(3)4种添发;见下图,答案不唯一.(4)由图可知该几何体最多有10个正方体,几何体A只有6个小正方体,10-6=4,所以最多可以添加4个正方体.【点睛】本题考查了物体的三视图,中等难度,培养看图能力、空间感是解题关键.28.(本题8分)(2022秋·江苏扬州·七年级校考阶段练习)用小立方块搭一个几何体,使它从正面和上面看到的形状如下图所示,从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数,请问:(1)俯视图中b=__________,a=__________.(2)这个几何体最少由__________个小立方块搭成.(3)能搭出满足条件的几何体共__________种情况,请在所给网格图中画出小立方块最多时几何体的左视图.(为便于观察,请将视图中的小方格用斜线阴影标注,示例:).【答案】(1)1;3(2)9(3)7【详解】试题分析:(1)由主视图可知,第2列小正方体个数都为1,所以b=1,,第三列小正方体个数为3,所以a=3;(2)正方体个数最少时,第一列正方体个数为:1+1+2=4个,第2列正方体个数为:1+1=2个,第3列正方体个数为:3个,一共有:4+2+3=9个;(3)第2列正方体个数确定为:1+1=2个,第3列正方体个数确定为:3个,第1列正方体情况可能为:①d=1,e=1,f=2;②d=1,e=2,f=1;③d=2,e=1,f=1;④d=2,e=2,f=1;⑤d=2,e=1,f=2;⑥d=1,e=2,f=2;⑦d=2,e=2,f=2,共7种情况,当d=2,e=2,f=2时小立方块最多,左视图如图所示.试题解析:(1)b=1,a=3;(2)1+1+2+1+1+3=9个;(3)共7种情况,当d=2,e=2,f=2时小立方块最多.此时,左视图为:点睛:掌握三视图的画法,并会根据三视图判断对应的正方体的个数.
相关资料
更多









