山西省运城市运康中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案

这是一份山西省运城市运康中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，某次知识竞赛共有20道题，规定，下列说法正确的是，牛顿曾说过，若分式有意义，的值可以是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．以下列各组线段为边作三角形，不能构成直角三角形的是（ ）
A．3，5，6B．3，4，5C．5，12，13D．9，40，41
2．已知：点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，则（m+n）2019的值为（ ）
A．0B．1C．﹣1D．32019
3．点P（1，﹣2）关于y轴对称的点的坐标是（ ）
A．（1，2）B．（﹣1，2）C．（﹣1，﹣2）D．（﹣2，1）
4．若a－2b=1，则代数式a2－2ab－2b的值为（ ）
A．－1B．0C．1D．2
5．某次知识竞赛共有20道题，规定：每答对一道题得＋5分，每答错一道题得－2分，不答的题得0分．已知圆圆这次竞赛得了60分，设圆圆答对了x道题，答错了y道题，则( )
A．x－y＝20B．x＋y＝20
C．5x－2y＝60D．5x＋2y＝60
6．下列说法正确的是（ ）
A．对角线互相垂直且相等的四边形是菱形B．对角线相等的四边形是矩形
C．对角线互相垂直的四边形是平行四边形D．对角线相等且互相平分的四边形是矩形
7．语句“的与的和不超过”可以表示为（ ）
A．B．C．D．
8．牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于60°”时，第一步先假设（ ）
A．三角形中有一个内角小于60°
B．三角形中有一个内角大于60°
C．三角形中每个内角都大于60°
D．三角形中没有一个内角小于60°
9．若分式有意义，的值可以是（ ）
A．1B．0C．2D．－2
10．如图，已知，那么添加下列一个条件后，仍无法判定的是（ ）
A．B．C．D．
11．在平面直角坐标系中，点A（﹣1，2）关于x轴对称的点B的坐标为（ ）
A．（﹣1，2）B．（1，2）C．（1，﹣2）D．（﹣1，﹣2）
12．已知实数x，y，z满足++＝，且＝11，则x+y+z的值为（ ）
A．12B．14C．D．9
二、填空题（每题4分，共24分）
13．若解分式方程产生增根，则__________．
14．三角形两边的中垂线的交点到三个顶点的距离的大小关系是_____．
15．若式子在实数范围内有意义，则的取值范围是__________．
16．已知一次函数y＝kx+b（k≠0）的图象与x轴交于（﹣5，0），则关于x的一元一次方程kx+b＝0的解为_____．
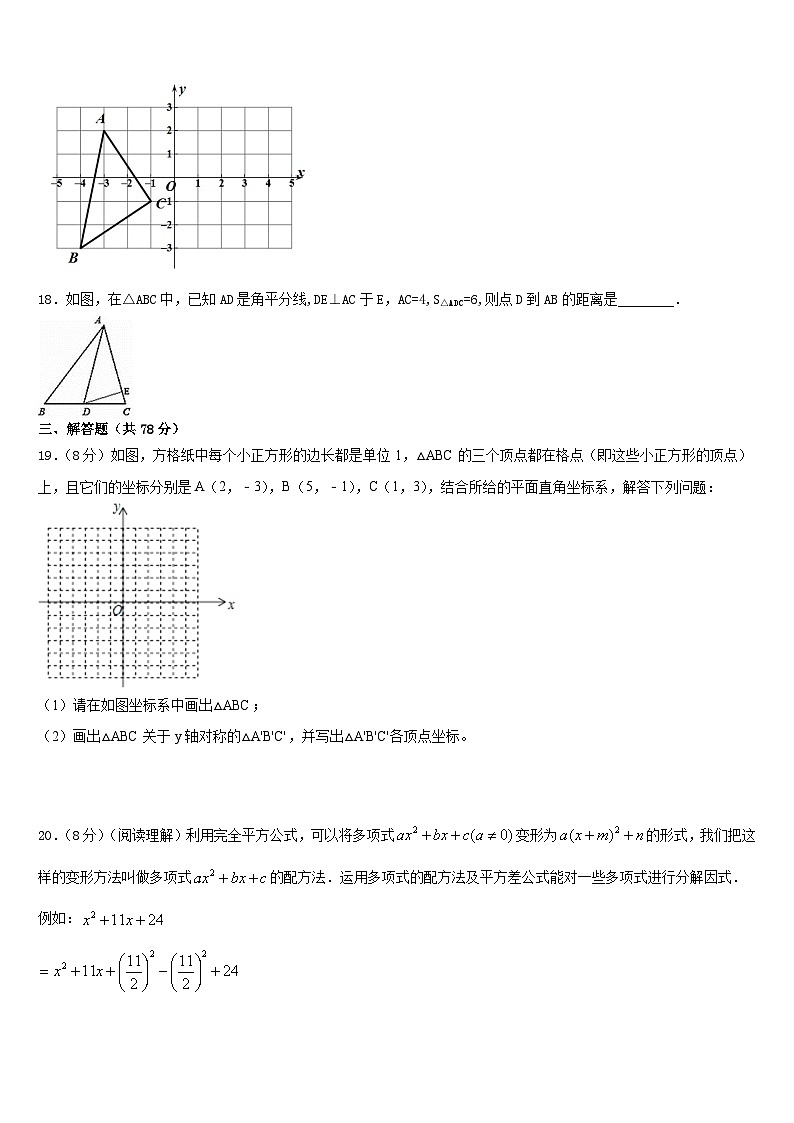
17．，，点在格点上，作出关于轴对称的，并写出点的坐标为________．
18．如图，在△ABC中，已知AD是角平分线,DE⊥AC于E，AC=4,S△ADC=6,则点D到AB的距离是________．
三、解答题（共78分）
19．（8分）如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点（即这些小正方形的顶点）上，且它们的坐标分别是A（2，﹣3），B（5，﹣1），C（1，3），结合所给的平面直角坐标系，解答下列问题：
（1）请在如图坐标系中画出△ABC；
（2）画出△ABC关于y轴对称的△A'B'C'，并写出△A'B'C'各顶点坐标。
20．（8分）（阅读理解）利用完全平方公式，可以将多项式变形为的形式，我们把这样的变形方法叫做多项式的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．
例如：
（问题解决）根据以上材料，解答下列问题：
（1）用多项式的配方法将多项式化成的形式；
（2）用多项式的配方法及平方差公式对多项式进行分解因式；
（3）求证：不论，取任何实数，多项式的值总为正数．
21．（8分）如图，四边形ABCD的顶点坐标为A（—5，1），B（—1，1）， C（—1，6），D（—5，4），请作出四边形ABCD关于x轴及y轴的对称图形，并写出坐标．
22．（10分）如图，已知四边形各顶点的坐标分别为．
（1）请你在坐标系中画出四边形，并画出其关于轴对称的四边形；
（2）尺规作图：求作一点，使得，且为等腰三角形．
（要求：仅找一个点即可，保留作图痕迹，不写作法）
23．（10分）化简求值：，其中，
24．（10分）如图1，点P、Q分别是边长为4cm的等边三角形ABC的边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s．
（1）连接AQ、CP交于点M，则在P，Q运动的过程中，证明≌；
（2）会发生变化吗？若变化，则说明理由，若不变，则求出它的度数；
（3）P、Q运动几秒时，是直角三角形？
（4）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则变化吗？若变化说明理由，若不变，则求出它的度数。
25．（12分）某中学有库存1800套旧桌凳，修理后捐助贫困山区学校．现有甲，乙两个木工组都想承揽这项业务．经协商后得知：甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的，甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天，甲木工组每天的修理费用是600元，乙木工组每天的修理费用是800元．
（1）求甲，乙两木工组单独修理这批桌凳的天数；
（2）现有三种修理方案供选择：方案一，由甲木工组单独修理这批桌凳；方案二，由乙木工组单独修理这批桌凳；方案三，由甲，乙两个木工组共同合作修理这批桌凳．请计算说明哪种方案学校付的修理费最少．
26．（12分）周末了，李芳的妈妈从菜市场买回来千克萝卜和千克排骨．
请你通过列方程组求出这天萝卜、排骨的售价分别是多少（单位：元千克）？
参考答案
一、选择题（每题4分，共48分）
1、A
2、B
3、C
4、C
5、C
6、D
7、A
8、C
9、C
10、C
11、D
12、A
二、填空题（每题4分，共24分）
13、-5.
14、相等
15、a＞﹣1
16、x＝﹣1．
17、(4，-3)．
18、3
三、解答题（共78分）
19、（1）图见解析；（2）图见解析；A′(-2，-3)，B′(-5，-1)，C′(-1，3)
20、（1），见解析；（2），见解析；（3）见解析
21、详见解析
22、见解析
23、-，-
24、（1）见解析；（2）∠CMQ=60°，不变；（3）当第秒或第2秒时，△PBQ为直角三角形；（4）∠CMQ=120°，不变．
25、（1）30,1；（2）第二种方案学校付的修理费最少．
26、这个月萝卜的售价是元千克，排骨的售价是元千克