广西北流、陆川、容县2023-2024学年八上数学期末教学质量检测模拟试题含答案

这是一份广西北流、陆川、容县2023-2024学年八上数学期末教学质量检测模拟试题含答案，共7页。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题（每题4分，共48分）
1．下列命题属于真命题的是（ ）
A．同旁内角相等，两直线平行B．相等的角是对顶角
C．平行于同一条直线的两条直线平行D．同位角相等
2．若不等式的解集是，则的取值范围是（ ）
A．B．C．D．
3．在和中，①，②，③，④，⑤，⑥，则下列各组条件中使和全等的是（ ）
A．④⑤⑥B．①②⑥C．①③⑤D．②⑤⑥
4．若是完全平方式，则实数的值为（ ）
A．B．C．D．
5．如图，在△PAB中，∠A=∠B，D、E、F分别是边PA、PB、AB上的点，且AD=BF，BE=AF．若∠DFE=34°，则∠P的度数为（ ）
A．112°B．120°C．146°D．150°
6．不等式2x－1≤5的解集在数轴上表示为（ ）
A．B．C．D．
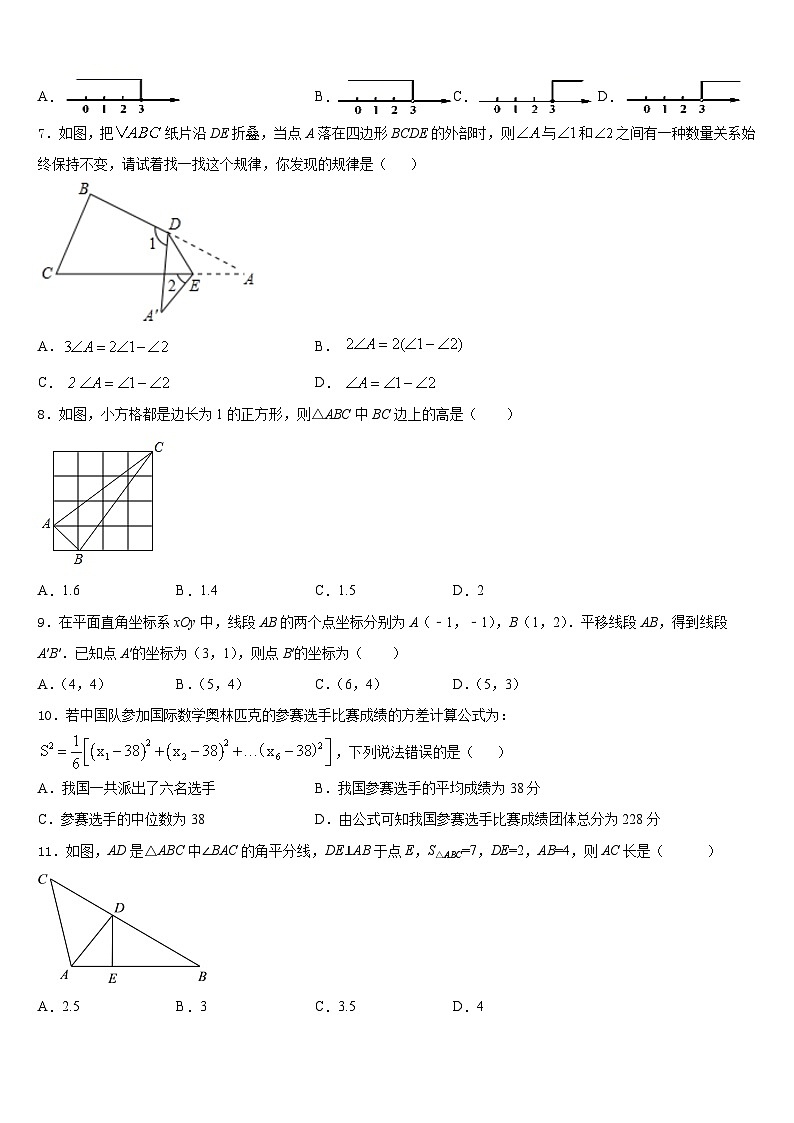
7．如图，把纸片沿DE折叠，当点A落在四边形BCDE的外部时，则与和之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）
A．B．
C．D．
8．如图，小方格都是边长为1的正方形，则△ABC中BC边上的高是（ ）
A．1.6B．1.4C．1.5D．2
9．在平面直角坐标系xOy中，线段AB的两个点坐标分别为A（﹣1，﹣1），B（1，2）．平移线段AB，得到线段A′B′．已知点A′的坐标为（3，1），则点B′的坐标为（ ）
A．（4，4）B．（5，4）C．（6，4）D．（5，3）
10．若中国队参加国际数学奥林匹克的参赛选手比赛成绩的方差计算公式为：，下列说法错误的是（ ）
A．我国一共派出了六名选手B．我国参赛选手的平均成绩为38分
C．参赛选手的中位数为38D．由公式可知我国参赛选手比赛成绩团体总分为228分
11．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（ ）
A．2.5B．3C．3.5D．4
12．已知，那么＝（ ）
A．6B．7C．9D．10
二、填空题（每题4分，共24分）
13．点和关于轴对称，则_____．
14．使代数式有意义的x的取值范围是_____．
15．分解因式：4mx2﹣my2=_____．
16．如图，在△ABC中，∠ACB=90°，CD是高，∠A=30°，若AB=20，则BD的长是 ．
17．如图，点分别在线段上，与相交于点，已知，若要判断则需添加条件__________．（只要求写出一个）
18．已知a，b互为相反数，并且3a－2b＝5，则a2＋b2＝________．
三、解答题（共78分）
19．（8分）计算
（1）4（a﹣b）2﹣（2a+b）（2a﹣b）．
（2）先化简，再求值（a+2﹣）÷，其中a＝1
20．（8分）（1）先化简，再求值：，其中
（2）解分式方程：
21．（8分）为方便市民出行，减轻城市中心交通压力，青岛市掀起一轮城市基础设施建设高潮，动工修建贯穿东西、南北的地铁1、2、3、11号线．已知修建地铁2号线32千米和3号线66千米共投资581.6亿元，且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元．
（1）求2号线、3号线每千米的平均造价分别是多少亿元？
（2）除地铁1、2、3、11号线外，青岛市政府规划未来五年，还要再建182千米的地铁线网．据预算，这182千米地铁线网每千米的平均选价是2号线每千米的平均造价的1.2倍，则还需投资多少亿元？
22．（10分）如图，△ABC和△ADE分别是以BC，DE为底边且顶角相等的等腰三角形，点D在线段BC上，AF平分DE交BC于点F，连接BE，EF．
（1）CD与BE相等？若相等，请证明；若不相等，请说明理由；
（1）若∠BAC=90°，求证：BF1+CD1=FD1．
23．（10分）在△ABC中，BC=AC，∠C=90°，直角顶点C在x轴上，一锐角顶点B在y轴上．
（1）如图①若AD于垂直x轴，垂足为点D．点C坐标是（-1，0），点A的坐标是（-3，1），求点B的坐标．
（2）如图②，直角边BC在两坐标轴上滑动，若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴于E，请猜想BD与AE有怎样的数量关系，并证明你的猜想．
（3）如图③，直角边BC在两坐标轴上滑动，使点A在第四象限内，过A点作AF⊥y轴于F，在滑动的过程中，请猜想OC，AF，OB之间有怎样的关系?并证明你的猜想．
24．（10分）（1）计算：
（2）分解因式：
25．（12分）如图是10×8的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长都是1个单位，线段的端点均在格点上，且点的坐标为，按下列要求用没有刻度的直尺画出图形．
（1）请在图中找到原点的位置，并建立平面直角坐标系；
（2）将线段平移到的位置，使与重合，画出线段，然后作线段关于直线对称线段，使的对应点为，画出线段；
（3）在图中找到一个各点使，画出并写出点的坐标．
26．（12分）如图1，在正方形ABCD（正方形四边相等，四个角均为直角）中，AB＝8，P为线段BC上一点，连接AP，过点B作BQ⊥AP，交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交AD于点N．
（1）求证：BP＝CQ；
（2）若BP＝PC，求AN的长；
（3）如图2，延长QN交BA的延长线于点M，若BP＝x（0＜x＜8），△BMC'的面积为S，求S与x之间的函数关系式．
参考答案
一、选择题（每题4分，共48分）
1、C
2、C
3、D
4、C
5、A
6、A
7、C
8、B
9、B
10、C
11、B
12、B
二、填空题（每题4分，共24分）
13、
14、x≥0且x≠2
15、m（2x+y）（2x﹣y）
16、1
17、答案不唯一，如
18、2
三、解答题（共78分）
19、（1）﹣8ab+5b2；（2），﹣．
20、（1），8；（2）原方程无解
21、（1）2号线每千米的平均造价为5.8亿元，3号线每千米的平均造价为1亿元；（2）还需投资1211.72亿元
22、（1）CD=BE，理由见解析；（1）证明见解析.
23、（1）点B的坐标是（0，2）；（2）BD=2AE，证明见解析；（3）OC=OB+AF，证明见解析．
24、（1）；（2）
25、（1）见解析；（2）见解析；（3）见解析G（）
26、（1）见解析；（2）1.2；（3）