广西柳州市城中学区2023-2024学年数学八上期末联考模拟试题含答案

这是一份广西柳州市城中学区2023-2024学年数学八上期末联考模拟试题含答案，共8页。试卷主要包含了近似数0.13是精确到，已知二元一次方程组，则的值为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．下列各组数据中的三个数作为三角形的边长，其中不能构成直角三角形的是（ ）
A．3，4，5B．，，C．8，15，17D．5，12，13
2．9的平方根是( )
A．±B．3C．±81D．±3
3．如图，，，与相交于点.则图中的全等三角形共有( )
A．6对B．2对C．3对D．4对
4．如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）
A．甲B．乙C．丙D．丁
5．四边形ABCD中，若∠A+∠C+∠D=280°，则∠B的度数为( )
A．80° B．90° C．170° D．20°
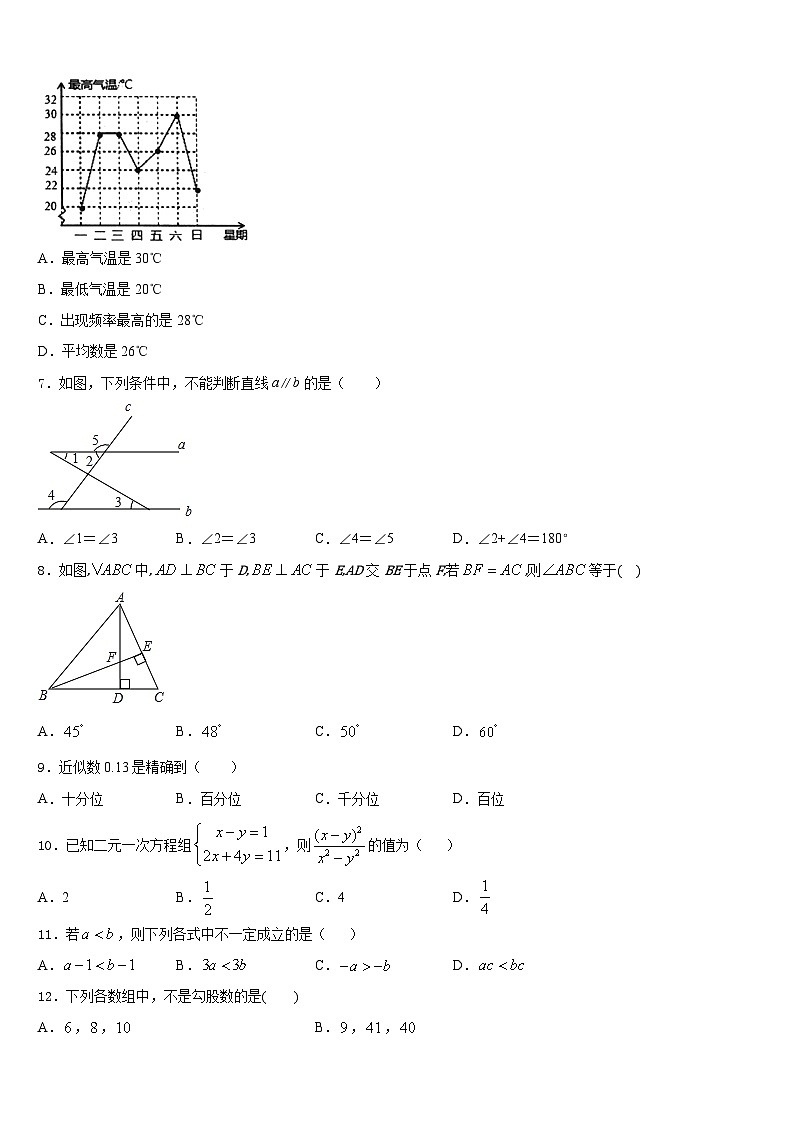
6．如图，是宜宾市某周内最高气温的折线统计图，关于这7天的日气温的说法，错误的是（ ）
A．最高气温是30℃
B．最低气温是20℃
C．出现频率最高的是28℃
D．平均数是26℃
7．如图，下列条件中，不能判断直线a∥b的是（ ）
A．∠1＝∠3B．∠2＝∠3C．∠4＝∠5D．∠2+∠4＝180°
8．如图,中,于D,于E,AD交BE于点F,若,则等于( )
A．B．C．D．
9．近似数0.13是精确到（ ）
A．十分位B．百分位C．千分位D．百位
10．已知二元一次方程组，则的值为（ ）
A．2B．C．4D．
11．若，则下列各式中不一定成立的是（ ）
A．B．C．D．
12．下列各数组中，不是勾股数的是( )
A．，，B．，，
C．，，D．，，（为正整数）
二、填空题（每题4分，共24分）
13．现定义一种新的运算：，例如：，则不等式的解集为 .
14．∠A=65º，∠B=75º，将纸片一角折叠，使点C落在△ABC外，若∠2=20º，则∠1的度数为 _______.
15．如图，在△ABC中，∠ACB=90°，∠BAC=40°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为____________．
16．市运会举行射击比赛，射击队从甲、乙、丙、丁四人中选拔一人参赛．在选拔赛中，每人射击10次，计算他们10次成绩（单位：环）的平均数及方差如下表．根据表中提供的信息，你认为最合适的人选是_____，理由是_________．
17．游泳者在河中逆流而上，于桥A下面将水壶遗失被水冲走，继续前游30分钟后他发现水壶遗失，于是立即返回追寻水壶，在桥A下游距桥1.2公里的桥B下面追到了水壶，那么该河水流的速度是_________．
18．一个多边形的内角和是外角和的倍，那么这个多边形的边数为_______.
三、解答题（共78分）
19．（8分）问题情景：如图1，在同一平面内，点和点分别位于一块直角三角板的两条直角边，上，点与点在直线的同侧，若点在内部，试问，与的大小是否满足某种确定的数量关系？
（1）特殊探究：若，则_________度，________度，_________度；
（2）类比探索：请猜想与的关系，并说明理由；
（3）类比延伸：改变点的位置，使点在外，其它条件都不变，判断（2）中的结论是否仍然成立？若成立，请说明理由；若不成立，请直接写出，与满足的数量关系式．
20．（8分）如图是4×4正方形网格，其中已有3个小方格涂成了黑色．现在要从其余13个白色小方格中选出一个也涂成黑色，使整个涂成黑色的图形成为轴对称图形，这样的白色小方格有多少个?请分别在下图中涂出来，并画出这个轴对称图形的对称轴．
21．（8分）运动会结束后八（1）班班主任准备购买一批明信片奖励积极参与运动会各个比赛项目的学生，计划用班费180元购买A、B两种明信片共20盒，已知A种明信片每盒12元，B种明信片每盒8元．
（1）根据题意，甲同学列出了尚不完整的方程组如下：；请在括号内填上具体的数字并说出a，b分别表示的含义，甲：a表示__________，b表示_______________；
（2）乙同学设了未知数但不会列方程，请你帮他把方程补充完整并求出该方程组的解；
乙：x表示购买了A种明信片的盒数，y表示购买了B种明信片的盒数．
22．（10分）如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长，交y轴于点E．
（1）求证：△OBC≌△ABD；
（2）若以A，E，C为顶点的三角形是等腰三角形，求点C的坐标．
23．（10分）如图，在中，，，平分，，求证：
24．（10分）已知：直线，为图形内一点，连接，．
（1）如图①，写出，，之间的等量关系，并证明你的结论；
（2）如图②，请直接写出，，之间的关系式；
（3）你还能就本题作出什么新的猜想？请画图并写出你的结论（不必证明）．
25．（12分）如图，在中，于D
（1）若，求的度数
（2）若点E在AB上，EF//AC交AD的延长线于点F
求证：AE=FE
26．（12分）如图，已知△ABC三个顶点的坐标分别A（-2,3）、B（-6,0）、C（-1,0）.
（1） 画出△ABC关于y轴对称的图形，并写出点B的对应点B1的坐标；
（2）在y轴上找出点M,使MA+MC最小，请画出点M (写出画图过程，用虚线保留画图痕迹)
参考答案
一、选择题（每题4分，共48分）
1、B
2、D
3、D
4、A
5、A
6、D
7、B
8、A
9、B
10、D
11、D
12、C
二、填空题（每题4分，共24分）
13、
14、100°
15、20°或40°或70°或100°
16、丁； 综合平均数和方差两个方面说明丁成绩既高又稳定
17、0.01km/min
18、1
三、解答题（共78分）
19、（1）125，90，35；（2）∠ABP+∠ACP=90°-∠A，证明见解析；（3）结论不成立．∠ABP-∠ACP=90°-∠A，∠ABP+∠ACP=∠A-90°或∠ACP - ∠ABP =90°-∠A．
20、4个，详见解析
21、（1），a表示A种明信片的总价，b表示B种明信片的总价；
（2）见解析．
22、（1）见解析；（2）以A，E，C为顶点的三角形是等腰三角形时，点C的坐标为（3，0）
23、详见解析
24、（1），见解析；（2）；（3），见解析
25、（1）50°；（2）见解析
26、答案见解析
甲
乙
丙
丁
平均数（cm）
方差
甲
乙
丙
丁
平均数
8.3
8.1
8.0
8.2
方差
2.1
1.8
1.6
1.4