河南省驻马店市西平五中学2023-2024学年八上数学期末联考试题含答案

这是一份河南省驻马店市西平五中学2023-2024学年八上数学期末联考试题含答案，共8页。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
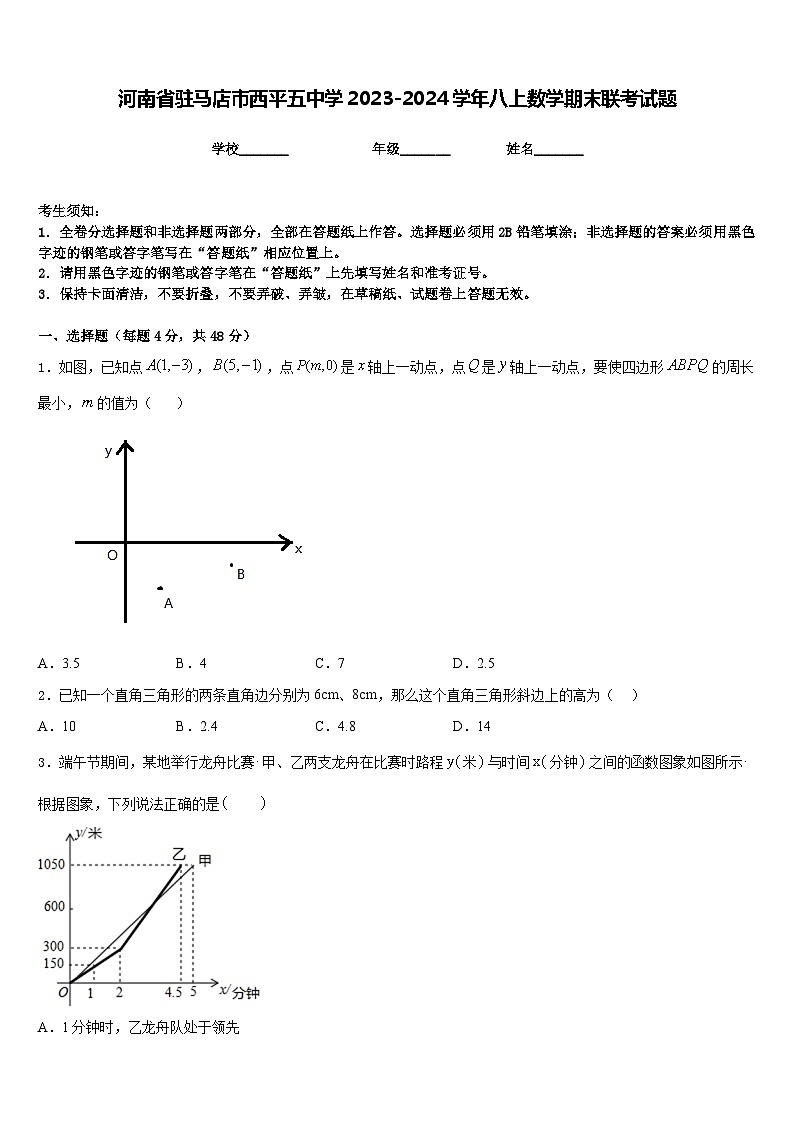
1．如图，已知点，，点是轴上一动点，点是轴上一动点，要使四边形的周长最小，的值为（ ）
A．3.5B．4C．7D．2.5
2．已知一个直角三角形的两条直角边分别为6cm、8cm，那么这个直角三角形斜边上的高为（ ）
A．10B．2.4C．4.8D．14
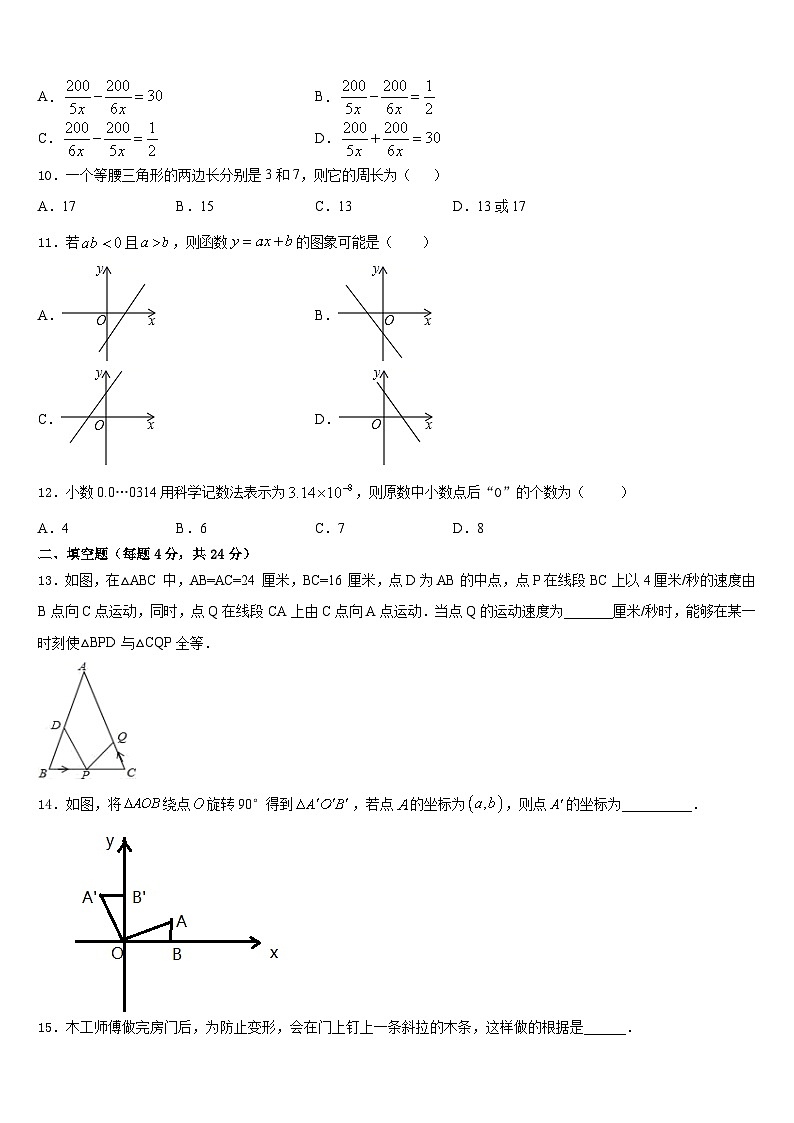
3．端午节期间，某地举行龙舟比赛甲、乙两支龙舟在比赛时路程米与时间分钟之间的函数图象如图所示根据图象，下列说法正确的是
A．1分钟时，乙龙舟队处于领先
B．在这次龙舟赛中，甲支龙舟队比乙支龙舟队早分钟到达终点
C．乙龙舟队全程的平均速度是225米分钟
D．经过分钟，乙龙舟队追上了甲龙舟队
4． “厉害了，中国华为！”2019年1月7日，华为宣布推出业界最高性能ARM-based处理器—鲲鹏1．据了解，该处理器采用7纳米制造工艺．已知1纳米=0.000000001米，则7纳米用科学记数法表示为（ ）
A．米B．米C．米D．米
5．将下列多项式因式分解,结果中不含有因式(a+1)的是( )
A．a2-1
B．a2+a
C．a2+a-2
D．(a+2)2-2(a+2)+1
6．图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线（ ）
A．l1B．l2C．l3D．l4
7．如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=CD，过点B作BF∥DE，与AE的延长线交于点F，若AB=6，则BF的长为（ ）
A．6B．7C．8D．10
8．一个多边形的各个内角都等于120°，则它的边数为（ ）
A．3B．6C．7D．8
9．两地相距200千米，甲车和乙车的平均速度之比为5:6，两辆车同时从地出发到地，乙车比甲车早到30分钟，设甲车平均速度为千米/小时，则根据题意所列方程是（ ）
A．B．
C．D．
10．一个等腰三角形的两边长分别是3和7，则它的周长为（ ）
A．17B．15C．13D．13或17
11．若且，则函数的图象可能是（ ）
A．B．
C．D．
12．小数0.0…0314用科学记数法表示为，则原数中小数点后“0”的个数为（ ）
A．4B．6C．7D．8
二、填空题（每题4分，共24分）
13．如图，在△ABC中，AB=AC=24厘米，BC=16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为_______厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
14．如图，将绕点旋转90°得到，若点的坐标为，则点的坐标为__________．
15．木工师傅做完房门后，为防止变形，会在门上钉上一条斜拉的木条，这样做的根据是______．
16．有一个数值转换器，原理如图：当输入x为81时，输出的y的值是_____．
17．已知，为实数，等式恒成立，则 ____________．
18．某商店卖水果，数量x(千克)与售价y(元)之间的关系如下表，(y是x的一次函数)
当x=7千克时，售价y=______元.
三、解答题（共78分）
19．（8分）已知，．
（1）求的值；
（2）求的值；
（3）求的值．
20．（8分）解答下列各题
（1）如图1，已知OA＝OB，数轴上的点A所表示的数为m，且|m+n|＝2
①点A所表示的数m为 ；
②求代数式n2+m﹣9的值．
（2）旅客乘车按规定可以随身携带一定质量的行李，如果超过规定，则需购买行李票，设行李票y（元）是行李质量x（千克）的一次函数，其图象如图2所示．
①当旅客需要购买行李票时，求出y与x之间的函数关系式；
②如果张老师携带了42千克行李，她是否要购买行李票？如果购买需买多少行李票？
21．（8分）将图1中的矩形ABCD沿对角线AC剪开，再把△ABC沿着AD方向平移，得到图2中的△A′BC′．
（1）在图2中，除△ADC与△C′BA′全等外，请写出其他2组全等三角形；① ；② ；
（2）请选择（1）中的一组全等三角形加以证明．
22．（10分）某校开展以“倡导绿色出行，关爱师生健康”为主题的教育活动．为了了解本校师生的出行方式，在本校范围内随机抽查了部分师生，已知随机抽查的教师人数为学生人数的一半，将收集的数据绘制成下列不完整的两种统计图．
（1）本次共调查了多少名学生？
（2）求学生步行所在扇形的圆心角度数．
（3）求教师乘私家车出行的人数．
23．（10分）已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，
（1）证明ABDF是平行四边形；
（2）若AF=DF=5，AD=6，求AC的长．
24．（10分）如图，，，于点．求证：．
25．（12分）如图，在等腰△ABC中，AC＝BC，D，E分别为AB，BC上一点，∠CDE＝∠A．
（1）如图1，若BC＝BD，∠ACB＝90°，则∠DEC度数为_________°；
（2）如图2，若BC＝BD，求证：CD＝DE；
（3）如图3，过点C作CH⊥DE，垂足为H，若CD＝BD，EH＝1，求DE－BE的值．

26．（12分）如图，AD是△ABC的中线，AB＝AC＝13，BC＝10，求AD长．
参考答案
一、选择题（每题4分，共48分）
1、A
2、C
3、D
4、A
5、C
6、C
7、C
8、B
9、B
10、A
11、A
12、C
二、填空题（每题4分，共24分）
13、4或6
14、
15、三角形具有稳定性
16、
17、－12
18、22.5元
三、解答题（共78分）
19、（1）19；（2）；（3）
20、（1）①﹣；②3或﹣5；（2）①y＝x﹣5；②她要购买行李票，需买2元的行李票．
21、（1）△AA′E≌△C′CF；△A′DF≌△CBE；（2）见解析.
22、（1）60名；（2）72°；（3）15
23、（1）证明见解析；（2）．
24、证明见解析．
25、（1）67.5;（1）证明见解析；（3）DE－BE=1．
26、1