

海北市重点中学2023-2024学年数学八年级第一学期期末检测试题含答案
展开
这是一份海北市重点中学2023-2024学年数学八年级第一学期期末检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每题4分,共48分)
1.若分式有意义,的值可以是( )
A.1B.0C.2D.-2
2.下列四个图形中,是轴对称图形的个数是( )
A.1B.2C.3D.4
3.64的平方根是( )
A.8B.C.D.32
4.(2011贵州安顺,4,3分)我市某一周的最高气温统计如下表:
则这组数据的中位数与众数分别是( )
A.27,28B.27.5,28C.28,27D.26.5,27
5.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为
A.B.3C.1D.
6.已知x2+16x+k是完全平方式,则常数k等于( )
A.64B.48C.32D.16
7.若关于x的分式方程=2的解为非负数,则m的取值范围是( )
A.m>﹣1B.m≥1C.m>﹣1且m≠1D.m≥﹣1且m≠1
8.我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A.B.C.D.
9.如图,阴影部分搪住的点的坐标可能是( )
A.(6,2)B.(-5,3)
C.(-3,-5)D.(4,-3)
10.禽流感病毒的形状一般为球形,直径大约为0.000000102米,用科学记数法表示为( )米
A.B.C.D.
11.下列运算中错误的是( )
①;②;③;④;⑤
A.②③B.①④C.②④D.③⑤
12.计算的结果是( )
A.B.C.D.
二、填空题(每题4分,共24分)
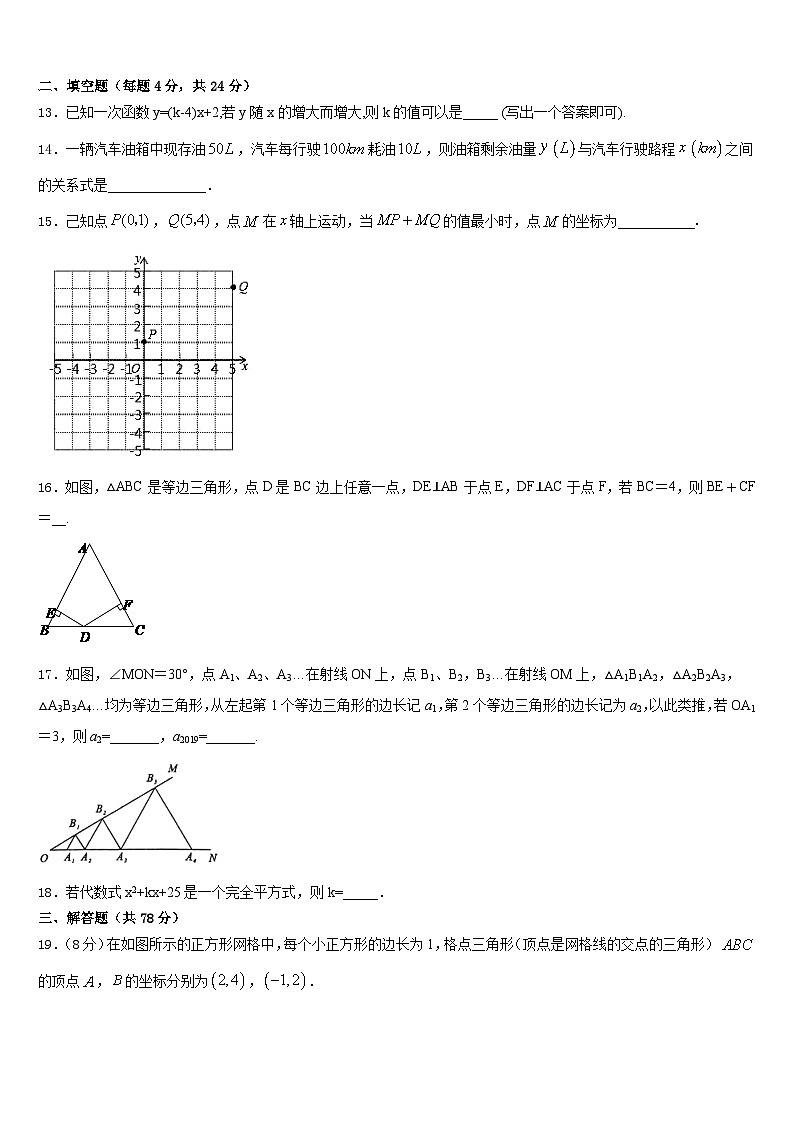
13.已知一次函数y=(k-4)x+2,若y随x的增大而增大,则k的值可以是_____ (写出一个答案即可).
14.一辆汽车油箱中现存油,汽车每行驶耗油,则油箱剩余油量与汽车行驶路程之间的关系式是______________.
15.己知点,,点在轴上运动,当的值最小时,点的坐标为___________.
16.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,若BC=4,则BE+CF=__.
17.如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记a1,第2个等边三角形的边长记为a2,以此类推,若OA1=3,则a2=_______,a2019=_______.
18.若代数式x2+kx+25是一个完全平方式,则k=_____.
三、解答题(共78分)
19.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)的顶点,的坐标分别为,.
(1)请在图中画出平面直角坐标系;
(2)请画出关于轴对称的;
(3)线段的长为_______.
20.(8分)如图,已知△ABC的三个顶点的坐标分别为A(-5,0)、B(-2,3)、C(-1,0).
(1)画出△ABC关于原点O成中心对称的图形△A′B′C′;
(2)将△ABC绕原点O顺时针旋转90°,画出对应的△A″B″C″,并写出点B″的坐标.
21.(8分)计算(每小题4分,共16分)
(1)
(2)已知.求代数式的值.
(1)先化简,再求值,其中.
(4)解分式方程:+1.
22.(10分)某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用6000元购进电冰箱的数量与用4800元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,现有两种进货方案①冰箱30台,空调70台;②冰箱50台,空调50台,那么该商店要获得最大利润应如何进货?
23.(10分)如图,正比例函数的图象和一次函数的图象交于点,点B为一次函数的图象与x轴负半轴交点,且的面积为1.
求这两个函数的解析式.
根据图象,写出当时,自变量x的取值范围.
24.(10分)先化简再求值:4(m+1)2-(2m+5)(2m-5),其中m=-1.
25.(12分)已知,如图,和都是等边三角形,且点在上.
(1)求证:
(2)直接写出和之间的关系;
26.(12分)在学习了轴对称知识之后,数学兴趣小组的同学们对课本习题进行了深入研究,请你跟随兴趣小组的同学,一起完成下列问题.
(1)(课本习题)如图①,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD. 求证:DB=DE
(2)(尝试变式)如图②,△ABC是等边三角形,D是AC边上任意一点,延长BC至E,使CE=AD.
求证:DB=DE.
(3)(拓展延伸)如图③,△ABC是等边三角形,D是AC延长线上任意一点,延长BC至E,使CE=AD请问DB与DE是否相等? 并证明你的结论.
参考答案
一、选择题(每题4分,共48分)
1、C
2、D
3、C
4、A
5、A
6、A
7、D
8、A
9、D
10、C
11、C
12、D
二、填空题(每题4分,共24分)
13、1
14、y=50-0.1x
15、(1,0)
16、1.
17、6; 3×1.
18、.
三、解答题(共78分)
19、(1)见解析;(2)见解析;(3).
20、见解析
21、(1)1;(2)7;(1);(4)
22、(1)每台电冰箱与空调的进价分别是2000元,1600元;(2)该商店要获得最大利润应购进冰箱30台,空调70台
23、 (1),;(2).
24、5
25、(1)证明见解析;(2)AE+AD=AB
26、(1)见详解;(2)见详解;(3)DB=DE成立,证明见详解
最高气温(℃)
25
26
27
28
天 数
1
1
2
3
相关试卷
这是一份淮北市重点中学2023-2024学年数学九上期末学业水平测试试题含答案,共8页。
这是一份海北市重点中学2023-2024学年九年级数学第一学期期末达标检测试题含答案,共8页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
这是一份2023-2024学年海北市重点中学数学九年级第一学期期末调研模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。










