2022-2023学年陕西省渭南市临渭区七年级（上）期末数学试卷（含解析）

这是一份2022-2023学年陕西省渭南市临渭区七年级（上）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1.−2的相反数是( )
A. 2B. −2C. 12D. −12
2.用一个平面去截下列几何体，截面不可能是三角形的是( )
A. B.
C. D.
3.2022年4月28日，京杭大运河实现全线通水．京杭大运河是中国古代劳动人民创造的一项伟大工程，它南起余杭(今杭州)，北到涿郡(今北京)，全长约1800000m.将1800000用科学记数法表示应为( )
A. 0.18×107B. 1800×103C. 18×105D. 1.8×106
4.如图，某同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长小，能正确解释这一现象的数学知识是( )
A. 两点之间，直线最短
B. 两点确定一条直线
C. 两点之间，线段最短
D. 经过一点有无数条直线
5.下列调查方式，你认为最合适的是( )
A. 为了了解同学们对央视《主持人大赛》栏目的喜爱程度，小华在学校随机采访了10名七年级学生
B. 咸阳机场对旅客上飞机进行安检，采用抽样调查方式
C. 为了了解西安市七年级学生的身高情况，采用抽样调查方式
D. 为了了解我省居民的日平均用电量，采用抽样调查方式
6.已知|a−6|+(b+8)2=0，则a−b的值为( )
A. −14B. 14C. −2D. 2
7.根据等式的性质，下列变形错误的是( )
A. 若a=b，则2a=2bB. 若2a=3b，则2a−2=3b−2
C. 若ac=bc，则a=bD. 若a5=b5，则2a=2b
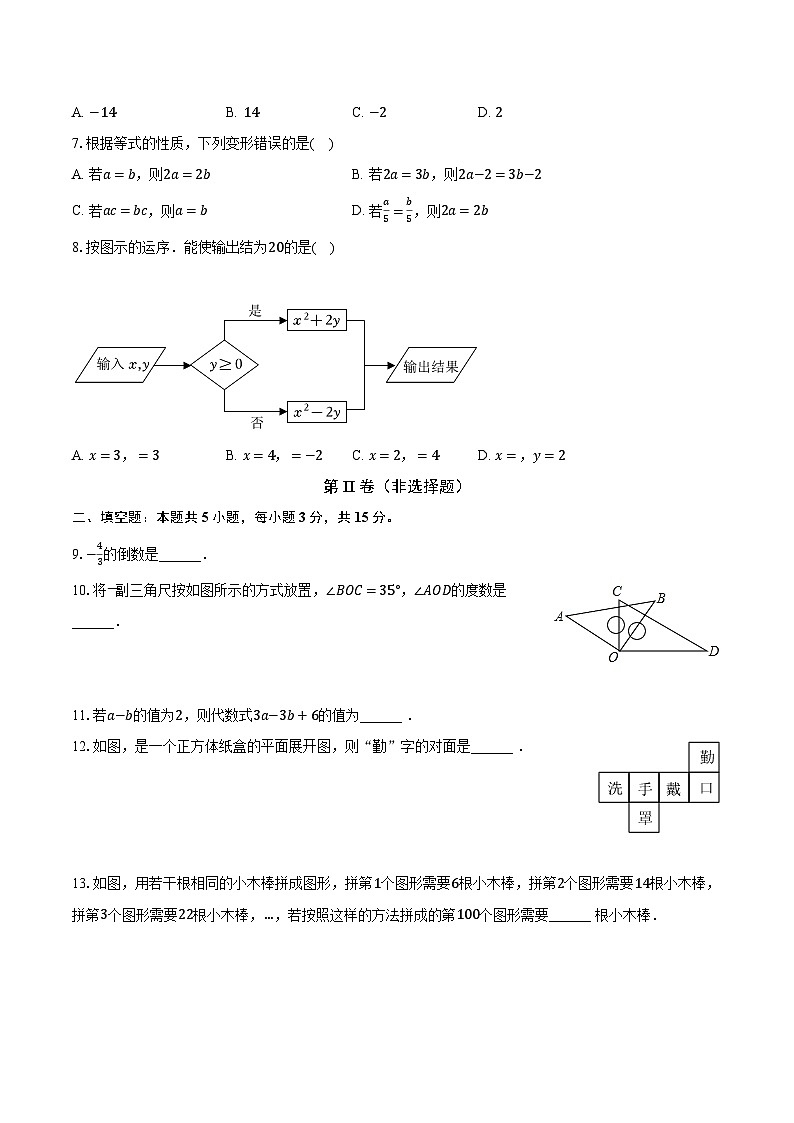
8.按图示的运序．能使输出结为20的是( )
A. x=3，=3B. x=4，=−2C. x=2，=4D. x=，y=2
第II卷（非选择题）
二、填空题：本题共5小题，每小题3分，共15分。
9.−43的倒数是______．
10.将⼀副三角尺按如图所示的方式放置，∠BOC=35°，∠AOD的度数是______．
11.若a−b的值为2，则代数式3a−3b+6的值为______ ．
12.如图，是一个正方体纸盒的平面展开图，则“勤”字的对面是______ ．
13.如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒，…，若按照这样的方法拼成的第100个图形需要______ 根小木棒．
三、计算题：本大题共1小题，共5分。
14.已知2x2y2m+5和与−xny是同类项，化简后求代数式2(mn−3m2)−(mn+6m2)+2mn的值．
四、解答题：本题共12小题，共76分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题5分)
计算：−12022+(−5)2÷(−53)−|−1−5|．
16.(本小题5分)
解方程：x+24−1=3−2x6．
17.(本小题5分)
在平整的地面上，有一个由若干个相同的小立方块搭成的几何体，如图所示．
(1)请依次画出从正面、左面、上面看这个几何体得到的图形；
(2)现在还有一些相同的小立方块，如果要保持从上面和左面看到的图形不变，那么最多可以添加几个这样的小立方块？
18.(本小题5分)
对于有理数a、b，定义一种新的运算：a⊗b=a×b−a+b.例如：1⊗2=1×2−1+2．
(1)计算(−3)⊗4的值．
(2)计算[5⊗(−2)]⊗3的值．
19.(本小题5分)
如图，已知线段AB，延长线段AB至点C，使BC=2AB，延长线段BA至点D，使AD=13AB，点E是线段AC的中点，若AB=12，求线段DE的长．
20.(本小题5分)
如图所示，池塘边有块长为20米，宽为10米的长方形土地，现在将其余三面留出宽都是x米的小路，中间余下的长方形部分做菜地．
(1)用含x的式子表示菜地的周长．
(2)求当x=1米时，菜地的周长．
21.(本小题6分)
如果关于x的方程x=2x−3的解比关于x的方程4x−2m=3x+1的解小2，求m的值．
22.(本小题7分)
近两年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查，调查结果显示，支付方式有：A微信．B支付宝．C银行卡．D其他．该小组选取了某一超市一天之内购买者的支付方式进行统计，得到如下两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：
(1)本次调查中，一共调查了多少名购买者？
(2)补全条形统计图：“A微信”支付方式所在扇形的圆心角为______度；
(3)若该超市这一天内有2000名购买者，请你估计B种支付方式的购买者有多少人？
23.(本小题7分)
一船在两码头之间航行，顺水需4小时，逆水4个半小时后还差8千米，水流每小时2千米，求两码头之间的距离？
24.(本小题8分)
如图，A，O，B三点共线，OD平分∠COB，OE平分∠AOC．
(1)若∠COD=40°，求∠AOE的度数；
(2)若∠COE：∠COD=3：2，求∠COE的度数．
25.(本小题8分)
为了防治“新型冠状病毒”，某中学拟向厂家购买消毒剂和红外线测温枪，积极做好教室消毒和师生的测温工作．
(1)若按原价购买一瓶消毒剂和一支红外线测温枪共需要400元，已知一支测温枪的价格比一瓶消毒剂的价格的6倍还贵15元，求每瓶消毒剂和每支测温枪的价格．
(2)由于采购量大，厂家推出两种购买方案(如表)：
若学校有75个班级，计划每班配置1支红外线测温枪和20瓶消毒剂，则学校选择哪种购买方案的总费用更低？
26.(本小题10分)
如图，已知数轴上有A、B两点，点B在原点的右侧，到原点的距离为2，点A在点B的左侧，AB=18.动点P、Q分别从A、B两点同时出发，在数轴上匀速运动，它们的速度分别为3个单位长度/秒、1个单位长度/秒，设运动时间为t秒．
(1)点A表示的数为______，点B表示的数为______
(2)若动点P、Q均向右运动．当t=2时，点P对应的数是______，P、Q两点间的距离为______个单位长度．请问当t为何值时，点P追上点Q，并求出此时点P对应的数；
(3)若动点Q从B点向左运动到原点后返回到B点停止，动点P从A点向右运动，当点Q停止时，点P也停止运动．请直接写出当t为何值时，在PA、PB和AB三条线段中，其中一条线段的长度是另一条线段长度的3倍．
答案和解析
1.【答案】A
【解析】解：−2的相反数是2，
故选：A．
根据相反数的定义进行判断即可．
本题考查相反数，掌握相反数的定义是正确判断的前提．
2.【答案】B
【解析】解：A、用一个平面去截一个长方体的角，其截面是三角形；
B、用一个平面去截一个圆柱体，无论怎样，其截面都不可能是三角形；
C、用一个平面平行与三角形底面去截一个三棱柱，其截面是三角形；
D、用一个平面从上面顶点垂直去截一个圆锥，其截面是三角形．
故选：B．
利用截一个几何体的截面形状进行判断即可．
本题考查截一个几何体，掌握截面的形状是正确判断的前提．
3.【答案】D
【解析】解：1800000=1.8×106．
故选：D．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|<10，n为整数，且n比原来的整数位数少1，据此判断即可．
此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|<10，确定a与n的值是解题的关键．
4.【答案】C
【解析】解：由于两点之间线段最短，
所以剩下树叶的周长比原树叶的周长小，
故选：C。
根据线段的性质，可得答案。
本题考查了线段的性质，利用线段的性质是解题关键。
5.【答案】D
【解析】解：A、为了了解同学们对央视《主持人大赛》栏目的喜爱程度，小华在学校随机采访了10名七年级学生，样本不具有代表性，故A错误；
B、咸阳机场对旅客上飞机进行安检，应该采用普查，故B错误；
C、为了了解西安市七年级学生的身高情况，应该采用普查，故C错误；
D、为了了解我省居民的日平均用电量，采用抽样调查方式，故D正确；
故选：D．
由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似求解．
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
6.【答案】B
【解析】解：∵|a−6|+(b+8)2=0，
∴a−6=0，b+8=0，
解得：a=6，b=−8，
∴a−b=6−(−8)=14．
故选：B．
根据绝对值和平方的非负性，可得a−6=0，b+8=0，从而得到a=6，b=−8，然后代入a−b即可求解．
本题主要考查了绝对值和平方的非负性、代数式求值，熟练掌握绝对值和平方的非负性是解题的关键．
7.【答案】C
【解析】解：A.根据等式的基本性质，若a=b，则2a=2b，故A正确，那么A不符合题意；
B.根据等式的基本性质，若2a=3b，得2a−2=3b−2，故B正确，那么B不符合题意；
C.根据等式的基本性质，由ac=bc，当c≠0，得a=b，故C错误，那么C符合题意；
D.根据等式的基本性质，若a5=b5，则2a=2b，故D正确，那么D不符合题意．
故选：C．
根据等式的基本性质解决此题．
本题主要考查等式的基本性质，熟练掌握等式的基本性质是解决本题的关键．
8.【答案】B
【解析】解：x=，y=，输出结果为3+23=15不符合题意；
x=2，y=时输结果为2+2×=12不符合题意；
x=−y=−2时，输出结果为(−4)22×(2=2，合题意；
故选：
根据算程序，结合出果确定的值可．
本题考查代数式的值与理数的混合运算掌运算则是解题关键．
9.【答案】−34
【解析】解：−43的倒数是−34，
故答案为：−34．
根据乘积为1的两个数互为倒数，可得一个数的倒数．
本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．
10.【答案】145°
【解析】【分析】
此题主要考查学生对角的计算的理解和掌握，解答此题的关键是让学生通过观察图示，发现几个角之间的关系．由△AOB与△COD为直角三角形得到∠AOB=∠COD=90°，则∠BOD=∠COD−∠BOC=90°−35°=55°，然后利用角与角之间的和差关系即可得到∠AOD的度数．
【解答】
解：∵∠AOB=∠COD=90°，∠BOC=35°，
∴∠BOD=∠COD−∠BOC=90°−35°=55°，
∴∠AOD=∠AOB+∠BOD=90°+55°=145°．
故答案为145°．
11.【答案】12
【解析】解：∵a−b=2，
∴3a−3b+6
=3(a−b)+6
=3×2+6
=12．
故答案为：12．
观察题中的两个代数式a−b和3a−3b+6，可以发现，3a−3b=3(a−b)，因此可整体代入即可求解．
本题考查了代数式求值，掌握整体代入法求代数式的值是关键．
12.【答案】罩
【解析】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
“勤”字的对面是“罩”．
故答案为：罩．
正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答即可．
本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
13.【答案】798
【解析】解：由题意知，第1个图形需要6根小木棒，
第2个图形需要6×2+2=14根小木棒，
第3个图形需要6×3+2×2=22根小木棒，
按此规律，第n个图形需要6n+2(n−1)=(8n−2)根小木棒，
当n=100时，8n−2=8×100−2=798．
故答案为：798．
根据图形的变化及数值的变化找出变化规律，即可得出结论．
本题考查了规律型中图形的变化类，解决该题型题目时，根据给定图形中的数据找出变化规律是关键．
14.【答案】解：∵2x2y2m+5和−xny是同类项，
∴n=2，2m+5=1，
∴m=−2，n=2，
2(mn−3m2)−(mn+6m2)+2mn
=2mn−6m2−mn−6m2+2mn
=3mn−12m2，
把m=−2，n=2代入上式得：
上式=3×(−2)×2−12×(−2)2=
=−12−12×4
=−12−48
=−60．
【解析】根据2x2y2m+5和−xny是同类项，列式计算m、n的值，整式去括号，合并同类项化为最简的形式，再把m、n的值代入计算即可．
本题考查同类项、整式的加减—化简求值，掌握同类项的定义及整式的加减—化简求值的步骤，先化简，再把给定字母的值代入计算，是解题关键．
15.【答案】解：原式=−1+25×(−35)−6
=−1−15−6
=−22．
【解析】根据有理数的混合运算法则求解即可．
本题考查了有理数的混合运算，解题的关键是掌握运算法则和运算顺序．
16.【答案】解：x+24−1=3−2x6，
去分母得：3(x+2)−12=2(3−2x)，
去括号得：3x+6−12=6−4x，
移项得：3x+4x=6+12−6，
合并同类项得：7x=12，
系数化为1得：x=127．
【解析】方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
本题主要考查解一元一次方程，解题的关键是掌握解一元一次方程的基本步骤：去分母、去括号、移项、合并同类项、系数化为1．
17.【答案】解：(1)如图所示：
(2)要保持从上面和左面看到的图形不变，最多可以添加 3个这样的小立方块．
【解析】(1)由已知条件可知，主视图有3列，每列小正方形数目分别为3，2，2；左视图有3列，每列小正方形数目分别为3，2，1；俯视图有3列，每列小正方数形数目分别为3，2，1.据此可画出图形；
(2)保持从上面和左面看到的图形不变，可往第二列前面的几何体上放一个小正方体，后面的几何体上放2个小正方体．
此题主要考查了三视图，正确掌握不同视图的观察角度是解题关键．
18.【答案】解：(1)由题意可得，
(−3)⊗4
=(−3)×4−(−3)+4
=−12+3+4
=−5；
(2)由题意可得，
[5⊗(−2)]⊗3
=[5×(−2)−5+(−2)]⊗3
=(−10−5−2)⊗3
=(−17)⊗3
=(−17)×3−(−17)+3
=−51+17+3
=−31．
【解析】(1)根据a⊗b=a×b−a+b，可以计算出所求式子的值；
(2)根据a⊗b=a×b−a+b，可以对所求式子计算，先计算中号内的，化简后，再计算括号外的．
本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．
19.【答案】解：∵BC=2AB，AD=13AB，AB=12，
∴BC=12×2=24，AD=12×13=4，
∴AC=AB+BC=12+24=36，DC=AC+AD=36+4=40．
∵点E是AC的中点，
∴EC=12AC=36×12=18，
∴DE=DC−CE=40−18=22．
【解析】先根据线段的比例得到BC和AD的长，再根据线段的和差得到DC和CE的长，进而可得答案．
本题考查两点间的距离，解题关键是熟练掌握中点的性质和线段和差的运算．
20.【答案】(1)解：设菜地的长a米，菜地的宽b米，
菜地的长a=(20−2x)米，
菜地的宽b=(10−x)米，
所以菜地的周长为2(20−2x+10−x)=(60−6x)米．
(2)解：当x=1时，菜地的周长C=60−6×1=54米．
【解析】(1)本题可先根据所给的图形，得出菜地的长和宽，然后根据长方形周长；
(2)直接将x=2代入第一问所求的周长式子中，得出结果．
本题主要考查列代数式和代数式求值．能够从生活实际中出发，以数学知识解决生活实际中的问题是解题的关键，同时也考查了长方形周长的计算．
21.【答案】解：解方程x=2x−3，得x=3．
∵关于x的方程x=2x−3的解比关于x的方程4x−2m=3x+1的解小2，
∴方程4x−2m=3x+1的解为x=5．
将x=5代入方程4x−2m=3x+1中，
得4×5−2m=3×5+1，
解得m=2，
∴m的值为2．
【解析】先解方程x=2x−3，求出x=3，然后根据关于x的方程x=2x−3的解比关于x的方程4x−2m=3x+1的解小2得到方程4x−2m=3x+1的解，然后代入4x−2m=3x+1求解即可．
此题考查了解一元一次方程和一元一次方程的解，正确掌握解一元一次方程的步骤是解题的关键．
22.【答案】(1)一共调查的购买者人数为：56÷28%=200(人)
答：本次调查中，一共调查了200名购买者；
(2)补全条形统计图如图所示：
“A微信”支付方式所在扇形的圆心角为108度；
(3)B种支付方式的购买者：2000×28%=560，
答：B种支付方式的购买者有560人．
【解析】解：(1)见答案；
(2)D类人数为：200×20%=40(人)，
则A类人数为：200−56−44−40=60，
“A微信”支付方式所在扇形的圆心角为：360°×60200×100%=108°，
故答案为108；
(3)见答案；
(1)根据B类人数及其所占的百分比计算；
(2)求出D类人数，补全条形统计图；根据“A微信”支付方式的百分比求出所在扇形的圆心角；
(3)B种支付方式的购买者的百分比，估计2000名购买者，B种支付方式的购买者的人数．
本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．
23.【答案】解：设两码头之间的距离为x千米，
根据题意得：x4−2=x−84.5+2，
解得x=80，
答：两码头之间的距离为80千米．
【解析】设两码头之间的距离为x千米，根据静水速度不变可得：x4−2=x−84.5+2，即可解得答案．
本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列方程．
24.【答案】解：(1)∵∠COD=40°，OD平分∠C0B，
∴∠BOC=2∠COD=80°，
又∵∠AOB=180°，
∴∠AOC=∠AOB−∠BOC=100°，
又∵OE平分∠AOC
∴∠AOE=12∠AOC=50°；
(2)∵OE平分∠AOC，OD平分∠COB，
∴∠COD=12∠BOC，∠COE=12∠AOC，
∴∠EOD=∠COE+∠COD=12∠AOC+12∠BOC=12×180°=90°，
又∵∠COE：∠COD=3：2，
∴∠COE=33+2∠EOD=35×90°=54°．
【解析】(1)根据角平分线定义得出∠BOC=2∠COD=80°，求出∠AOC，再根据角平分线定义得出即可；
(2)根据角平分线定义得出∠COD=12∠BOC，∠COE=12∠AOC，求出∠EOD=90°，再根据∠COE：∠COD=3：2求出∠COE即可．
本题考查了角平分线的定义，角的计算等知识点，能根据角平分线的定义得出∠COD=12∠BOC、∠COE=12∠AOC、∠BOC=2∠COD是解此题的关键．
25.【答案】解：(1)设每瓶消毒剂的价格是x元，则每支测温枪的价格是(6x+15)元，
根据题意得：x+(6x+15)=400，
解得x=55，
所以6x+15=6×55+15=345(元)，
答：每瓶消毒剂的价格是55元，则每支测温枪的价格是345元；
(2)学校一共需购买消毒剂75×20=1500(瓶)，
方案A费用：55×0.85×1500+345×0.9×(75−1500100)=70125+18630=88755(元)，
方案B费用：75×345×0.8+1500×55×0.85=90825(元)，
因为88755<90825，
所以学校选择A购买方案的总费用更低．
【解析】(1)设每瓶消毒剂的价格是x元，则每支测温枪的价格是(6x+15)元，可得：x+(6x+15)=400，即可解得答案；
(2)求出两种购买方案的费用，再比较即可．
本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列方程．
26.【答案】解：(1)−16，2；
(2)−10，14；
当点P追上点Q时，可得点P与点Q表示的数相同，
∴−16+3t=2+t，
∴t=9，
∴−16+3t=−16+27=11，
∴此时点P对应的数为11，
即当t为9时，点P追上点Q，此时点P对应的数为11；
(3)当Q停止时，所用的时间为4秒，
分四种情况：
当PB=3PA时，
18−3t=3×3t，
解得：t=1.5，
当PA=3PB时，
3t=3(18−3t)，
解得：t=4.5(舍去)，
当AB=3PA时，
18=3×3t，
解得：t=2，
当AB=3PB时，
18=3(18−3t)，
解得：t=4，
综上所述：当t为1.5秒或2秒或4秒时，在PA、PB和AB三条线段中，其中一条线段的长度是另一条线段长度的3倍．
【解析】【分析】
本题考查了数轴，列代数式，一元一次方程的应用，熟练掌握数轴上两点间距离是解题的关键，同时渗透了分类讨论的数学思想．
(1)根据点A与点B在数轴上的位置，即可解答；
(2)根据题意求出点P与点Q运动的路程，从而求出点P与点Q表示的数，即可求出P、Q两点间的距离，当点P追上点Q时，可得点P与点Q表示的数相同，从而得出关于t的方程，解方程即可解答；
(3)根据题意可知，当Q停止时，所用的时间为4秒，分四种情况：当PB=3PA时，当PA=3PB时，当AB=3PA时，当AB=3PB时，列出关于t的方程进行计算即可解答．
【解答】
解：(1)∵点B在原点的右侧，到原点的距离为2，
∴点B表示的数为2，
∵点A在点B的左侧，AB=18，
∴2−18=−16，
∴点A表示的数为−16，
故答案为：−16，2；
(2)当t=2时，3×2=6，1×2=2，
∴点P向右运动了6个单位长度，点Q向右运动了2个单位长度，
∴−16+6=−10，2+2=4，
∴点P对应的数是−10，点Q对应的数是4，
∴4−(−10)=4+10=14，
∴P、Q两点间的距离为14个单位长度，
故答案为：−10，14；
(3)见答案．购买方案
红外线测温枪
消毒剂
优惠
A
9折
8.5折
每购100瓶消毒剂送1支测温枪
B
8折
8.5折
无