人教A版 (2019)选择性必修 第二册第四章 数列4.3 等比数列优秀练习

这是一份人教A版 (2019)选择性必修 第二册第四章 数列4.3 等比数列优秀练习，文件包含第04讲431等比数列的概念原卷版docx、第04讲431等比数列的概念解析版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

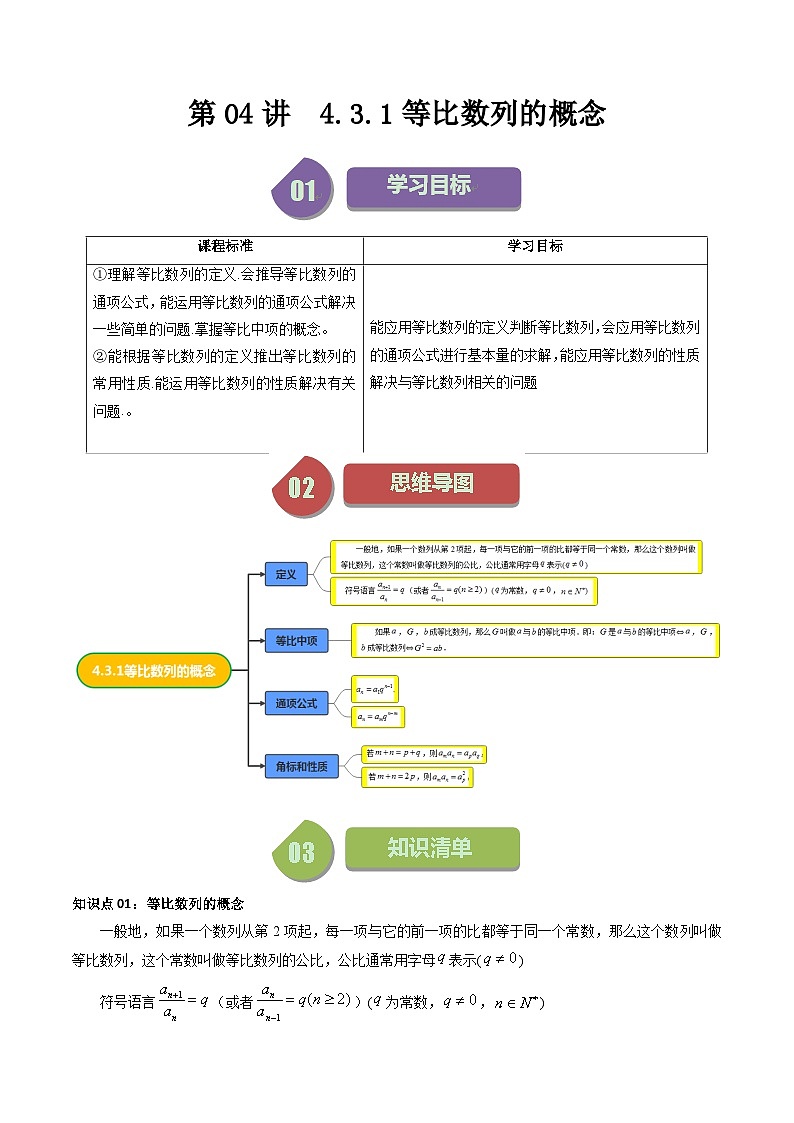
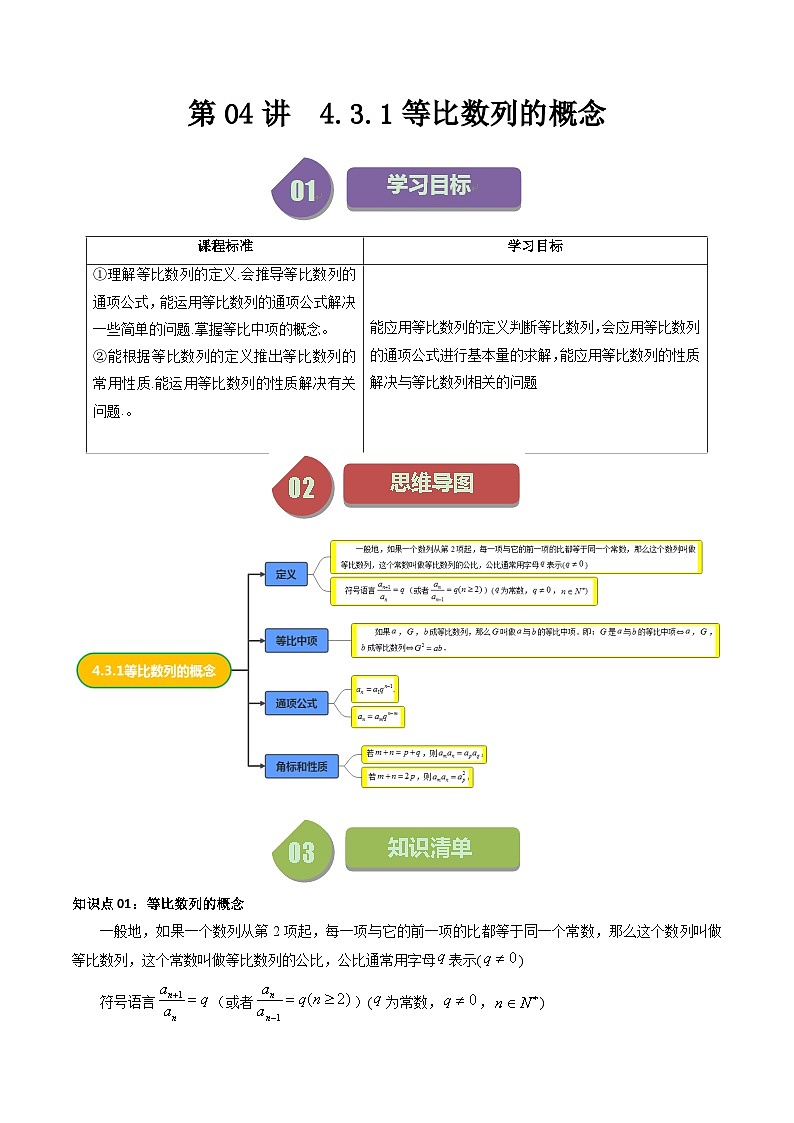
知识点01：等比数列的概念
一般地，如果一个数列从第2项起，每一项与它的前一项的比都等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母表示()
符号语言（或者）(为常数，，)
知识点02：等比中项
如果，，成等比数列，那么叫做与的等比中项．即：是与的等比中项⇔，，成等比数列⇔.
【即学即练1】（2023秋·福建漳州·高二校考阶段练习）在等比数列中，，则（ ）
A．B．C．D．
【答案】D
【详解】由，∴．
故选：D
知识点03：等比数列的通项公式
一般地，对于等比数列的第项有公式.这就是等比数列的通项公式，其中为首项，为公比．
知识点04：等比数列的单调性
已知等比数列的首项为，公比为
1、当或时，等比数列为递增数列；
2、当或时，等比数列为递减数列；
3、当时，等比数列为常数列（）
4、当时，等比数列为摆动数列.
【即学即练2】（2023春·高二课时练习）已知为等比数列，则“”是“为递增数列”的（ ）
A．必要而不充分条件B．充分而不必要条件
C．既不充分也不必要条件D．充要条件
【答案】A
【详解】当公比且时，，，此时，，不递增，充分性不成立，
当等比数列为递增数列时，，显然必要性成立.
综上所述：“”是“为递增数列”的必要而不充分条件.
故选：A
知识点05：等比数列的判断（证明）
1、定义：（或者）（可判断，可证明）
2、等比中项法：验证（特别注意）（可判断，可证明）
3、通项公式法：验证通项是关于的指数型函数（只可判断）
知识点06：等比数列常用性质
设数列是等比数列，是其前项和．
（1）
(2)若，则，其中.特别地，若，则，其中.
(3)相隔等距离的项组成的数列仍是等比数列，即，，，…仍是等比数列，公比为().
(4)若数列，是两个项数相同的等比数列，则数列，和(其中，，是非零常数)也是等比数列．
【即学即练3】（2023秋·广东深圳·高三校考阶段练习）在等比数列中，若，则的公比（ ）
A．B．2C．D．4
【答案】B
【详解】是等比数列，
依题意，，所以.
故选：B
题型01 等比数列通项公式的应用
【典例1】（2023秋·福建宁德·高二福建省宁德第一中学校考阶段练习）记为数列的前项和，且，则 .
【答案】
【详解】①，当时，，解得，
当时，②，
①-②得，，
即，所以，
是首项为-1，公比是2的等比数列，故.
故答案为：
【典例2】（2023春·北京东城·高二统考期末）已知数列的首项，且，那么 ；数列的通项公式为 .
【答案】 4
【详解】由题意数列的首项，且，
那么；
由此可知，故，则数列为首项是，公比为2的等比数列，
故，首项也适合该式，
故答案为：4；
【典例3】（2023·全国·高二课堂例题）已知数列是公比为q的等比数列．
(1)若，，求的通项公式；
(2)若，，，求n．
【答案】(1)
(2)9
【详解】（1）由等比数列的通项公式可知，，
两式相除得，即．
所以．
因此，这个数列的通项公式是．
（2）因为，，
所以．
又，因此，即．
【变式1】（2023春·江苏南通·高二期末）已知数列的前n项和为，且满足，则数列的通项公式为（ ）
A．B．C．D．
【答案】C
【详解】当时，，
当时，，
因此数列是首项为1，公比为2的等比数列，，
故选：C.
【变式2】（2023·西藏日喀则·统考一模）已知各项均为正数的等比数列满足，且，则
【答案】
【详解】设等比数列的公比为，因为，所以，
又，所以，解得，即，所以.
故答案为:.
【变式3】（2023秋·高二课时练习）在等比数列中，
(1)已知，，求；
(2)已知，，，求；
(3)已知，，求；
(4)已知，，求．
【答案】(1)
(2)
(3)
(4)
【详解】（1）等比数列中，，，则.
（2）等比数列中，，，，由，可得.
（3）等比数列中，，，由，可得.
（4）等比数列中，，，由，可得.
题型02等比中项
【典例1】（2023秋·江苏宿迁·高三校考阶段练习）在等比数列中，，是方程的两根，则（ ）
A．B．C．或D．
【答案】A
【详解】由于，是方程的两根，
所以，
由于，所以为正数，
所以．所以．
故选：A.
【典例2】（2023·全国·高二随堂练习）若a，G，b成等比数列，则称G为a和b的等比中项．
(1)求45和80的等比中项；
(2)已知两个数和的等比中项是2k，求k．
【答案】(1)
(2)或
【详解】（1）设为45和80的等比中项，则，所以.
所以45和80的等比中项为
（2）两个数和的等比中项是，
所以，，，
解得或，此时，，满足题意，
所以或.
【变式1】（2023秋·山东潍坊·高三统考阶段练习）已知等差数列的公差不为0，若，，成等比数列，则这个等比数列的公比是（ ）
A．B．C．2D．4
【答案】B
【详解】等差数列,设公差为d，因为，，成等比数列，
故，
又因为公差不为0，，所以，
则这个等比数列的公比是.
故选：B
【变式2】（2023春·河南信阳·高二信阳高中校考阶段练习）已知数列是等比数列，函数的零点分别是，则（ ）
A．2B．C．D．
【答案】D
【详解】由题意可得所以，
故，且，
故选：D
题型03等比数列的判断与证明
【典例1】（2023·全国·高二专题练习）如果数列是等比数列，那么（ ）
A．数列是等比数列B．数列是等比数列
C．数列是等比数列D．数列是等比数列
【答案】C
【详解】对于C，设等比数列的公比为，则，
所以为非零常数，则数列是等比数列，故C正确；
对于ABD，取，则，数列是等比数列，
则，，，
故，，，
所以，则数列不是等比数列，故A错误.
而，，，显然，
所以数列不是等比数列，故B错误.
而，，，则，
所以数列不是等比数列，故D错误.
故选：C.
【典例2】（2023·高二课时练习）函数（为常数，且），数列是首项为4，公差为2的等差数列，求证：数列是等比数列．
【答案】证明见解析
【详解】数列是首项为4，公差为2的等差数列，
所以，，
可得，，且k>0，k≠1，
所以，∴数列是等比数列.
【典例3】（2023·全国·高二专题练习）已知数列满足，且，求的通项公式．
【答案】
【详解】解：由可得：，
因为，所以，
所以是以1为首项3为公比的等比数列，
所以，
所以．
【变式1】（2023·全国·高二专题练习）在数列中，，．
(1)求证：是等比数列；
(2)求数列的通项公式．
【答案】(1)证明详见解析；
(2).
【详解】（1）依题意，数列中，，，
所以，
所以数列是首项为，公比为的等比数列.
（2）由（1）得：数列是首项为，公比为的等比数列，
所以.
【变式2】（2023春·高二课时练习）已知数列中，，.证明：数列是等比数列；
【答案】证明见解析
【详解】证明：因为，，所以，
所以，，
又，所以为首项是4，公比为2的等比数列.
题型04等比数列性质的应用
【典例1】（2023·湖北黄冈·统考模拟预测）已知数列是正项等比数列，数列满足.若，（ ）
A．24B．32C．36D．40
【答案】C
【详解】因为是正项等比数列，，
所以，则，
所以
.
故选：C.
【典例2】（2023秋·湖北·高三校联考阶段练习）在正项等比数列中，，则的最小值是（ ）
A．12B．18C．24D．36
【答案】C
【详解】在正项等比数列中，，所以，
当且仅当即时，等号成立，即的最小值是24.
故选：C.
【典例3】（2023·江西·校联考二模）在正项等比数列中，与是方程 的两个根，则 .
【答案】5
【详解】因为与是方程 的两个根，所以，
因为为正项等比数列，所以，
所以，
故答案为：5.
【变式1】（2023秋·辽宁沈阳·高三新民市高级中学校考阶段练习）已知数列是等差数列，数列是等比数列，，且，则（ ）
A．B．C．D．
【答案】D
【详解】解：∵数列是等差数列，且，
∴，可得，则.
∵数列是等比数列，∴，又由题意，
∴，∴，
∴，
∴.
故选：D．
【变式2】（2023秋·重庆渝中·高三重庆巴蜀中学校考阶段练习）已知在等比数列中，，是方程的两个实数根，则 ．
【答案】
【详解】∵，是方程的两个实数根，∴，，
故，，根据等比数列的性质有：且，
故．
故答案为：
【变式3】（2023秋·甘肃白银·高二校考阶段练习）正项等比数列中，，则的值是 ．
【答案】8
【详解】因为正项等比数列中，，
所以
，
故答案为：8
题型05构造等比数列求通项公式（构造法求通项）
【典例1】（2023·全国·高三专题练习）已知数列，，，则数列的通项公式为 .
【答案】/
【详解】由得，又
故是以公比为2的等比数列，且首项为，因此，故,
故答案为：
【典例2】（2023·全国·高二专题练习）已知数列的首项，且满足．求数列的通项公式；
【答案】
【详解】∵，∴，∴.
又∵，故是以2为首项，2为公比的等比数列,
∴，则．
【典例3】（2023秋·甘肃白银·高二校考阶段练习）在数列中，，
(1)证明：数列是等比数列；
(2)若，，求数列的前n项和Sn．
【答案】(1)证明见解析
(2)
【详解】（1）证明：由得.
因为，所以，所以
所以数列是以4为首项，2为公比的等比数列.
（2）由（1）得，∴，.
∴
【变式1】（2023秋·福建福州·高二校联考期末）已知数列满足，证明为等比数列，并求的通项公式.
【答案】证明过程见详解，.
【详解】因为，所以，
又，所以数列是以2为首项，3为公比的等比数列，
则，所以
【变式2】（2023春·高二课时练习）数列满足.
(1)若，求证：为等比数列；
(2)求的通项公式．
【答案】(1)证明见解析
(2)
【详解】（1）由于，
所以，
即，
所以数列是首项为，公比为的等比数列.
（2）由（1）得，
所以.
【变式3】（2023·全国·高三专题练习）已知数列满足，.
(1)写出该数列的前项；
(2)求数列的通项公式.
【答案】(1)，，，，
(2)
【详解】（1），
，，，.
（2）由得：，又，
数列是以为首项，为公比的等比数列，
，
.
题型06等比数列在传统文化中的应用
1．（2023秋·江苏淮安·高三统考开学考试）谢尔宾斯基（Sierpinski）三角形是一种分形，它的构造方法如下：取一个实心等边三角形（如图1），沿三边中点的连线，将它分成四个小三角形，挖去中间小三角形（如图2），对剩下的三个小三角形继续以上操作（如图3），按照这样的方法得到的三角形就是谢尔宾斯基三角形．如果图1三角形的边长为2，则图4被挖去的三角形面积之和是（ ）

A．B．C．D．
【答案】D
【详解】第一种挖掉的三角形边长为，共个，面积为；
第二种挖掉的三角形边长为，共个，面积为，
第三种挖掉的三角形边长为，共个，
面积为，
故被挖去的三角形面积之和是.
故选：D
2．（2023·全国·高三专题练习）科赫曲线因形似雪花，又被称为雪花曲线.其构成方式如下：如图1将线段等分为线段，如图2.以为底向外作等边三角形，并去掉线段，将以上的操作称为第一次操作；继续在图2的各条线段上重复上述操作，当进行三次操作后形成如图3的曲线.设线段的长度为1，则图3中曲线的长度为（ ）

A．2B．C．D．3
【答案】C
【详解】依题意，一条线段经过一次操作，其长度变为原来的，
因此每次操作后所得曲线长度依次排成一列，构成以为首项，为公比的等比数列，
所以当进行三次操作后的曲线长度为.
故选：C
3．（2023·北京·高三专题练习）“十二平均律” 是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f，则第八个单音的频率为
A．B．
C．D．
【答案】D
【详解】分析：根据等比数列的定义可知每一个单音的频率成等比数列，利用等比数列的相关性质可解.
详解：因为每一个单音与前一个单音频率比为，
所以，
又，则
故选D.
4．（2023秋·福建三明·高三统考期末）在第24届北京冬奥会开幕式上，一朵朵六角雪花飘拂在国家体育场上空，畅想着“一起向未来”的美好愿景.如图是“雪花曲线”的一种形成过程：从一个正三角形开始，把每条边分成三等份，然后以各边的中间一段为底边分别向外作正三角形，再去掉底边，重复进行这一过程，若第1个图中的三角形的周长为3，则第4个图形的周长为 .

【答案】
【详解】由题意，当时，第1个图中的三角形的边长为，三角形的周长为；
当时，第2个图中“雪花曲线”的边长为，共有条边，
其“雪花曲线”周长为；
当时，第3个图中“雪花曲线”的边长为，共有条边，
其“雪花曲线”周长为；
当时，第4个图中“雪花曲线”的边长为，共有条边，
其“雪花曲线”周长为.
故答案为：.
A夯实基础 B能力提升
A夯实基础
一、单选题
1．（2023秋·广东江门·高三校联考阶段练习）设是等比数列，且，，则（ ）
A．24B．36C．48D．64
【答案】C
【详解】在等比数列中， 设公比为，
∵，，
∴，
∴，
故选：C.
2．（2023秋·西藏林芝·高三校考阶段练习）在等比数列中，，，则（ ）
A．B．C．D．
【答案】C
【详解】，，解得：.
故选：C.
3．（2023春·贵州黔东南·高二校考阶段练习）数列1，1，1，…，1，…必为（ ）
A．等差数列，但不是等比数列B．等比数列，但不是等差数列
C．既是等差数列，又是等比数列D．既不是等差数列，也不是等比数列
【答案】C
【详解】数列1，1，1，…，1，…是公差为0的等差数列，也是公比为1的等比数列.
故选：C.
4．（2023秋·河北石家庄·高三石家庄市第十八中学校考阶段练习）已知等比数列的各项均为正数，若，，则（ ）
A．B．C．27D．
【答案】D
【详解】设的公比为，则，，．
因为，所以，因为，所以，所以．
因为的各项均为正数，所以．因为，所以．
故选：D
5．（2023秋·重庆·高三校联考阶段练习）已知数列满足，若，则（ ）
A．B．C．12D．36
【答案】D
【详解】由可知数列是公比为的等比数列，
所以，
解得：.
故选：D.
6．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知公差不为的等差数列的前项和为，若，，成等比数列，则（ ）
A．B．C．D．
【答案】B
【详解】因为，，成等比数列，所以，
又，所以，
显然，所以，即，
所以，又，
所以.
故选：B
7．（2023秋·安徽·高三安徽省宿松中学校联考开学考试）分形几何是一门新兴学科，图1是长度为1的线段，将其三等分，以中间线段为边作无底边正三角形得到图2，称为一次分形；同样把图2的每一条线段重复上述操作得到图3，称为二次分形；……，则第5次分形后图形长度为（ ）

A．B．C．D．
【答案】C
【详解】图1的线段长度为，图2的线段长度为，图3的线段长度为，，
则一次分形长度为，二次分形长度为，，
次分形后线段的长度为，
故5次分形后长度为，
故选：C.
8．（2023秋·山东潍坊·高三校考阶段练习）正项等比数列中，，若，则的最小值等于（ ）
A．1B．C．D．
【答案】D
【详解】设的公比为，则，
因为，所以，解得或（舍去），
，故，即，
，
当且仅当，即时，等号成立，
故的最小值等于
故选：D
二、多选题
9．（2023春·山东淄博·高二校考阶段练习）已知数列的首项为4，且满足，则（ ）
A．为等差数列B．为递增数列
C．为等比数列D．的前项和
【答案】BCD
【详解】由可得，所以数列为等比数列，且公比为2，故A错误，C正确，
，由于均为单调递增的数列，且各项均为正数，所以为递增数列，B正确，
，设的前项和为，则，D正确，
故选：BCD
10．（2023秋·甘肃·高二校考阶段练习）下列命题中，正确的有（ ）
A．数列中，“”是“是公比为2的等比数列”的必要不充分条件
B．数列的通项为，若为单调递增数列，则
C．等比数列中，，是方程的两根，则
D．等差数列，的前n项和为分别为，，若，则
【答案】AD
【详解】A：因为当时，显然数列不可能是等比数列，
但是是公比为2的等比数列一定有成立，
因此选项A正确；
B：因为为单调递增数列，
所以有，
因为函数是减函数，所以，
因此选项B不正确；
C：因为在等比数列中，设公比为 ，，是方程的两根，
所以有，于是有，
而，
所以，因此选项C不正确；
D：因为等差数列，的前n项和为分别为，，
所以由，
因此选项D正确，
故选：AD
三、填空题
11．（2023·全国·高三专题练习）已知，，则通项公式 .
【答案】
【详解】，
因此数列是以为首项，为公比的等比数列，
因此，
故答案为：
12．（2023春·江西·高二统考期末）记等比数列的前n项和为，且，则 .
【答案】
【详解】当时，；当时，，
由数列是等比数列，则，则，解得.
故答案为：.
四、解答题
13．（2023秋·湖北·高三校联考阶段练习）数列的满足，，．
(1)求数列的通项公式；
(2)将数列中去掉数列的项后余下的项按原来的顺序组成数列，求数列的前50项和．
【答案】(1)
(2)1473
【详解】（1）因为，
所以，
又因为，
所以，，
所以数列是以2为首项，2为公比的等比数列，
则，即．
（2）由得，，
因为，
所以中要去掉数列的项有5项，
所以
．
14．（2023秋·江苏·高二专题练习）设各项都是正数的数列的前项和为，，且．
(1)求数列的通项公式；
(2)若，，求数列的通项公式．
【答案】(1)
(2)
【详解】（1）已知，得，
两式作差，得，即．
又数列的各项都是正数，所以，所以，
显然数列是以1为首项，1为公差的等差数列，
所以；
（2）由（1）得，故，
而，故是首项为，公比为3的等比数列，
所以，故.
B能力提升
1．（2023秋·安徽·高三安徽省马鞍山市第二十二中学校联考阶段练习）0.618是无理数的近似值，被称为黄金比值.我们把腰与底的长度比为黄金比值的等腰三角形称为黄金三角形.如图，是顶角为，底的第一个黄金三角形，是顶角为的第二个黄金三角形，是顶角为的第三个黄金三角形，是顶角为的第四个黄金三角形，那么依次类推，第2023个黄金三角形的周长大约为（ ）

A．B．C．D．
【答案】D
【详解】第一个黄金三角形的底为，由得腰长，
记第个黄金三角形的底边长为，当时，第个黄金三角形的底边长为，腰长为，
而第个黄金三角形的底边长为第个黄金三角形的腰长，则，
因此，各个黄金三角形的底边长依次排成一列得数列，是首项为2，公比为的等比数列，
第个黄金三角形的底边长，腰长为，
周长为
，
所以第2023个黄金三角形的周长大约为.
故选：D
2．（2023秋·黑龙江哈尔滨·高三哈尔滨工业大学附属中学校校考阶段练习）符号表示不超过实数的最大整数，如，.已知数列满足，，.若，为数列的前项和，则（ ）
A．B．C．D．
【答案】B
【详解】因为，则，且，
所以，数列是首项为，公比也为的等比数列，
所以，，①
由可得，且，
所以，数列为常数列，且，②
由①②可得，
因为，
，则，
所以，，所以，，
所以，，
所以，
，
因此，.
故选：B.
3．（2023春·黑龙江大庆·高二校考期末）已如公比不为1的等比数列中，存在，满足，则的最小值为（ ）
A．B．C．D．
【答案】B
【详解】设等比数列的公比为，因为，可得，即，
可得，且，
由，
因为，所以，，则，得到，
当且仅当时，即时取等号，所以的最小值为，
故选：B.
4．（2023秋·上海静安·高二校考阶段练习）已知数列的通项公式（，为正整数）.
(1)若，，成等差数列，求的值；
(2)是否存在且为正整数）与，使得，，成等比数列？若存在，求出所有满足条件的有序实数对；若不存在，请说明理由.
【答案】(1)
(2)存在，所有满足条件的有序实数对为，，，，，，，，
【详解】（1）由已知可得，，，.
因为，，成等差数列，
所以有，即，
整理可得，.
因为为正整数，所以.
（2）假设存在且为正整数）与，使得，，成等比数列.
因为，，，
所以由，，成等比数列可得，
，即，
整理可得，，
所以，是的正因数.
当，即时，；
当，即时，；
当，即时，；
当，即时，；
当，即时，；
当，即时，；
当，即时，；
当，即时，；
当，即时，.
所以，存在且为正整数）与，使得，，成等比数列.
所有满足条件的有序实数对，，，，，，，，.
5．（2023秋·高二课时练习）如图所示，有三根针和套在一根针上的若干金属片，按下列规则，把金属片从一根针上全部移到另一根针上．

（1）每次只移动个金属片；
（2）较大的金属片不能放在较小的金属片上面；
试推测：把个金属片从号针移动到号针，最少需要移动多少次？
【答案】
【详解】设是把个盘子从号针移到号针的最少移动次数，
当时，；
当时，小盘号，大盘号，小盘从号号，；
当时，用次把中小两盘移动到号，再将大盘移动到号，接着再用次把中小两盘从号转移到号，
；
以此类推，当且时，，
，又，
数列是以为首项，为公比的等比数列，
，，
经检验：满足，.
6．（2023·全国·高三专题练习）某景点上山共有999级台阶，寓意长长久久.甲上台阶时，可以一步上一个台阶，也可以一步上两个台阶，若甲每步上一个台阶的概率为，每步上两个台阶的概率为，为了简便描述问题，我们约定，甲从0级台阶开始向上走，一步走一个台阶记1分，一步走两个台阶记2分，记甲登上第n个台阶的概率为，其中，且. 证明：数列是等比数列.
【答案】证明见解析
【详解】证明：由题可得，，
则，，
∴，
由于，，∴，
故，则，
∴数列是以为首项，为公比的等比数列.
课程标准
学习目标
①理解等比数列的定义.会推导等比数列的通项公式，能运用等比数列的通项公式解决一些简单的问题.掌握等比中项的概念。
②能根据等比数列的定义推出等比数列的常用性质.能运用等比数列的性质解决有关问题.。
能应用等比数列的定义判断等比数列，会应用等比数列的通项公式进行基本量的求解，能应用等比数列的性质解决与等比数列相关的问题