数学选择性必修第二册第9章 统计本章综合与测试精品练习

这是一份数学选择性必修第二册第9章 统计本章综合与测试精品练习，文件包含第9章统计重点题型复习原卷版docx、第9章统计重点题型复习解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。


题型一 相关关系与函数关系辨识
【例1】（2023·高二课时练习）下列两个变量间的关系，是相关关系的是（ ）
A．任意实数和它的平方 B．圆半径和圆的周长
C．正多边形的边数和内角度数之和 D．天空中的云量和下雨
【答案】D
【解析】对于ABC，两个变量之间为确定性关系，
即两个变量之间均为函数关系，ABC错误；
对于D，根据生活经验，天空中的云量和下雨之间不是确定性关系，
虽然有云不一定下雨，但是如果没有云一定不下雨，
说明它们之间是相关关系，D正确.故选：D.
【变式1-1】（2023·高二课时练习）下列变量之间的关系是相关关系的是（ ）
A．正方体的表面积与体积
B．光照时间与果树的产量
C．匀速行驶车辆的行驶距离与时间
D．某运动会中某代表团的足球队的比赛成绩与乒乓球队的比赛成绩
【答案】B
【解析】对于A，正方体的体积确定，则表面积随之确定，是一种确定性关系，A错误；
对于B，光照时间越长，果树的产量相对越大，是一种线性相关关系，B正确；
对于C，行驶速度与时间是一种确定的函数关系，C错误；
对于D，足球比赛成绩与乒乓球比赛成绩没有关系，不具有相关关系，D错误.
故选：B
【变式1-2】（2022春·浙江·高二统考阶段练习）已知变量与近似满足关系，变量与负相关，则下列结论中正确的是（ ）
A．与负相关，与负相关 B．与正相关，与正相关
C．与负相关，与正相关 D．与正相关，与负相关
【答案】C
【解析】因为变量与近似满足关系，
又，所以与负相关，
又因为变量与负相关，所以与正相关.故选：C.
【变式1-3】（2022·高二课时练习）判断如图所示的图形中具有相关关系的是（ ）
A． B．
C． D．
【答案】C
【解析】根据图象可得A,B为连续曲线，变量间的关系是确定的，不是相关关系，
C中散点分布在一条直线附近，可得其线性相关，
D中散点分布在一个长方形区域，即非线性相关，故选：C
【变式1-4】（2022春·河南郑州·高二统考期末）成语“名师出高徒”可以解释为“知名老师指导出高水平学生的概率较大”，即教师的名声与学生的水平之间有关联．下列能描述出生活中两种属性或现象之间关联的成语是（ ）
A．登高望远 B．亡羊补牢 C．目瞪口呆 D．袖手旁观
【答案】A
【解析】成语“名师出高徒”的意思说有名的教师一定能教出高明的徒弟，
通常情况下，高水平的教师有很大的趋势教出高水平的学生，
所以教师的水平与学生的水平成正相关关系，
四个选项中只有“登高望远”满足题意，
即登高有很大的趋势可以看更远，登高和望远之间成正相关关系.故选：A.
题型二 相关系数的计算与应用
【例2】（2023·高二课时练习）在一组样本数据不全相等的散点图中，若所有样本点都在直线上，则这组样本数据的样本相关系数为（ ）
A． B．0 C．1 D．
【答案】A
【解析】这组样本数据的所有样本点都在直线上，
这组样本数据完全相关，
即说明这组数据的样本完全负相关，其相关系数是故选：A.
【变式2-1】（2023春·江苏南京·高二南京航空航天大学附属高级中学校考期中）已知四组不同数据的两变量的线性相关系数如下：数据组①的相关系数；数据组②的相关系数；数据组③的相关系数；数据组④的相关系数.则下列说法正确的是（ ）
A．数据组①对应的数据点都在同一直线上
B．数据组②中的两变量线性相关性最强
C．数据组③中的两变量线性相关性最强
D．数据组④中的两变量线性相关性最弱
【答案】B
【解析】对A，数据组①的相关系数，故数据组①对应的数据点无线性关系，故A错误；
对BC，数据组②的相关系数为4组中绝对值的最大值，
故数据组②中的两变量线性相关性最强，故B正确，C错误；
对D，数据组①的相关系数为4组中绝对值最小，
故数据组①中的两变量线性相关性最弱，故D错误故选：B
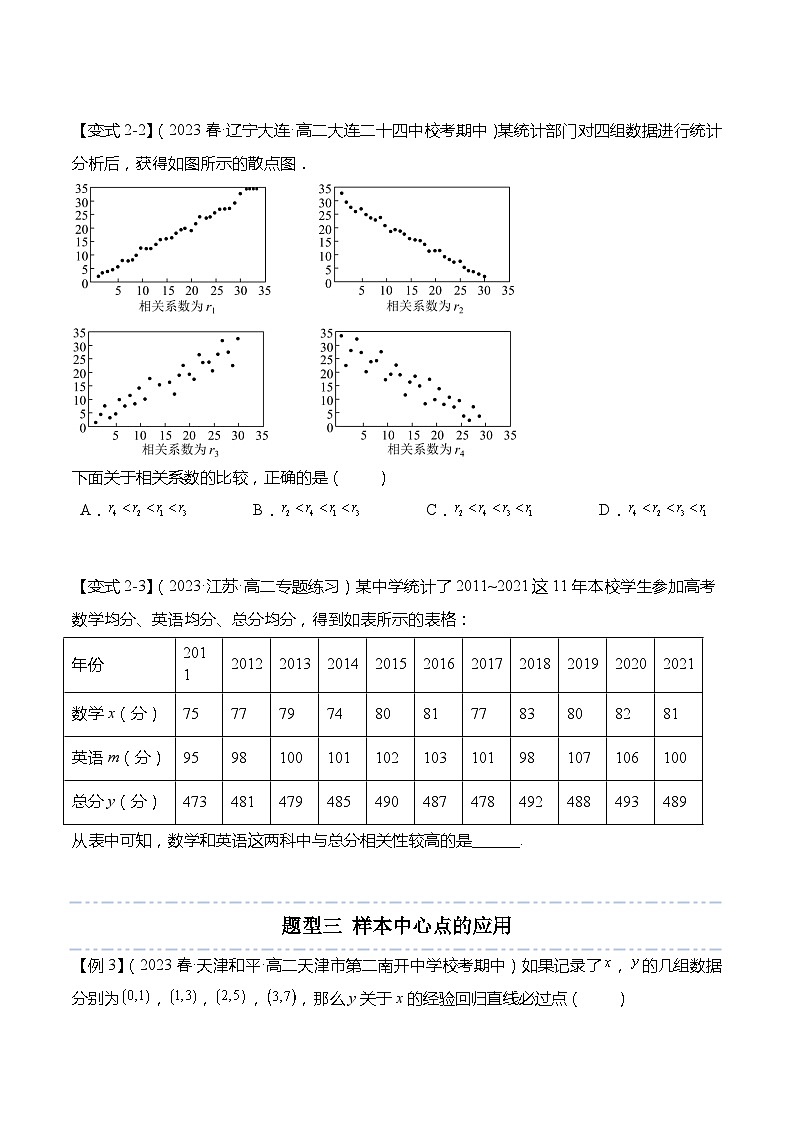
【变式2-2】（2023春·辽宁大连·高二大连二十四中校考期中）某统计部门对四组数据进行统计分析后，获得如图所示的散点图．
下面关于相关系数的比较，正确的是（ ）
A． B． C． D．
【答案】C
【解析】由图可知：所对应的图中的散点呈现正相关，
而且对应的相关性比对应的相关性要强，故，
所对应的图中的散点呈现负相关，且根据散点的分布情况可知,
因此，故选：C
【变式2-3】（2023·江苏·高二专题练习）某中学统计了2011~2021这11年本校学生参加高考数学均分、英语均分、总分均分，得到如表所示的表格：
从表中可知，数学和英语这两科中与总分相关性较高的是______.
【答案】数学
【解析】设数学学科和英语学科的相关系数分别为，，，，，
；
；
，
∴，∴.
；
，
∴，∴.
∵，∴从相关系数角度来考虑，数学学科与总分的相关性较高，
故答案为：数学.
题型三 样本中心点的应用
【例3】（2023春·天津和平·高二天津市第二南开中学校考期中）如果记录了，的几组数据分别为，，，，那么y关于x的经验回归直线必过点（ ）
A． B． C． D．
【答案】D
【解析】由已知，，
所以回归直线必过点．故选：D．
【变式3-1】（2023春·江西·高二江西师大附中校考阶段练习）经统计，用于数学学习的时间(单位：小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间与数学成绩进行数据收集如下:
由表中样本数据求得回归方程为，则点与直线的位置关系是（ ）
A．点在直线左侧 B．点在直线右侧 C．点在直线上 D．无法确定
【答案】C
【解析】由题得，，
代入回归方程得，
∴点在直线上.故选：C
【变式3-2】（2022秋·江西宜春·高三校联考期末）为了研究某班学生的脚长x（单位：厘米）和身高y（单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y与x之间有线性相关关系，设其回归直线方程为．已知，，．该班某学生的脚长为25，据此估计其身高为（ ）
A．167 B．174 C．176 D．180
【答案】B
【解析】由题设，，且，
所以，故回归直线为，
当厘米，则厘米.故选：B
【变式3-3】（2023春·湖南长沙·高二长沙市明德中学校考期中）蟋蟀鸣叫是大自然优美和谐的音乐，蟋蟀鸣叫的频率（单位：次/分钟）与气温（单位：℃）有较强的线性相关关系．某同学在当地通过观测，得到如下数据，并建立了关于的线性回归方程．当蟋蟀每分钟鸣叫52次时，该地当时的气温预报值为_______________．
【答案】33
【解析】依题意可得，，
又关于的线性回归方程，所以，解得，
所以回归方程为，当时，
即当蟋蟀每分钟鸣叫次时，该地当时的气温预报值为.
故答案为：
【变式3-4】（2023·北京·高三专题练习）“民生”供电公司为了分析“康居”小区的用电量y（单位）与气温x（单位：℃）之间的关系，随机统计了4天的用电量与当天的气温，这两者之间的对应关系见下表：
若上表中的数据可用回归方程来预测，则当气温为时该小区相应的用电量约为______．
【答案】
【解析】，
则，解得，
所以，
当时，，
即当气温为时该小区相应的用电量约为．
故答案为：.
题型四 线性回归分析
【例4】（2023·全国·高三专题练习）某专营店统计了近五年来该店的创收利润y（单位：万元）与时间（单位：年）的相关数据，列表如下：
依据表中给出的数据，是否可用线性回归模型拟合y与t的关系？请计算相关系数r并加以说明（计算结果精确到0.01，若，则认为y与t高度相关，可用线性回归模型拟合y与t的关系）．
【答案】， y与t高度相关，可用线性回归模型拟合y与t的关系.
【解析】由题知，，，
，，，
则，
，
y与t高度相关，可用线性回归模型拟合y与t的关系.
【变式4-1】（2023·全国·高三专题练习）规定抽球试验规则如下：盒子中初始装有白球和红球各一个，每次有放回的任取一个，连续取两次，将以上过程记为一轮．如果每一轮取到的两个球都是白球，则记该轮为成功，否则记为失败．在抽取过程中，如果某一轮成功，则停止；否则，在盒子中再放入一个红球，然后接着进行下一轮抽球，如此不断继续下去，直至成功．
（1）某人进行该抽球试验时，最多进行三轮，即使第三轮不成功，也停止抽球，记其进行抽球试验的轮次数为随机变量，求的分布列和数学期望；
（2）为验证抽球试验成功的概率不超过，有1000名数学爱好者独立的进行该抽球试验，记表示成功时抽球试验的轮次数，表示对应的人数，部分统计数据如下：
求关于的回归方程，并预测成功的总人数（精确到1）；
【答案】（1）分布列见解析，；（2），465
【解析】（1）由题知，的取值可能为1，2，3，
所以；
；
所以的分布列为：
所以数学期望为
（2）令，，，则，
由题知：，
，，
所以，
所以，，
故所求的回归方程为：，
所以，估计时，；
估计时，；
估计时，；
预测成功的总人数为.
【变式4-2】（2023·全国·高二专题练习）从某居民区随机抽取10个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，算得.
（1）求家庭的月储蓄对月收入的线性回归方程；
（2）判断变量与之间是正相关还是负相关；
（3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.
附：线性回归方程中，，，其中，为样本平均值.
【答案】（1）；（2）正相关；（3）（千元）.
【解析】（1）由题意知
，，
则，
.
所以所求回归方程为.
（2）因为，所以变量的值随的值增加而增加，故与之间是正相关.
（3）将代入回归方程，得，
则可以预测该家庭的月储蓄为（千元）.
【变式4-3】（2023春·四川成都·高二四川省成都市新都一中校联考期中）市场研究机构Cunterpint发布了最新全球电动汽车市场报告，2022年总计销量超1020万辆，比亚迪、特斯拉和大众集团位列排行榜前三.某电动汽车公司调研统计了之前5年（2018年到2022年）自己品牌电动汽车年销售量y（单位：万辆），并制作了如下表格.
（1）请根据表格中统计的数据作出散点图：
（2）记年份代码为x，2018年到2022年分别对应x=1，2，3，4，5，请根据散点图判断，模型①y=a+bx；②；③，哪一个更适合作为年销售量y关于年份代码x的回归方程（给出判断即可，不必说明理由）；
（3）根据（2）的判断结果，求出年销售量y关于年份代码x的回归方程，并预测今年（2023年）该公司电动汽车的年销售量.
参考数据：
参考公式：最小二乘估计公式：，.
【答案】（1）散点图见解析；（2）②更适合；（3），96.5万辆
【解析】（1）如图，
（2）根据散点图可知②更适合；
（3）令，则，，，，
对于回归方程，可得：，
，
∴回归方程为，即，
令x=6，得，
预测2023年该公司电动汽车的年销售量为96.5万辆.
题型五 非线性回归分析
【例5】（2023·全国·高三专题练习）一种高产新品种水稻单株穗粒数和土壤锌含量有关，现整理并收集了6组试验数据，（单位：粒）与土壤锌含量（单位：）得到样本数据，令，并将绘制成如图所示的散点图.若用方程对与的关系进行拟合，则（ ）
A． B． C． D．
【答案】C
【解析】因为，，令，则与的回归方程为，
根据散点图可知与正相关，
因此，又回归直线的纵截距小于0，即，得，
所以，.故诜：C
【变式5-1】（2023春·江苏南通·高三海安高级中学校考阶段练习）用模型拟合一组数据组，其中；设，得变换后的线性回归方程为，则（ ）
A． B．70 C． D．35
【答案】C
【解析】因为，所以，，
即，
所以.故选：C
【变式5-2】（2023·全国·高三专题练习）已知变量的关系可以用模型拟合，设，其变换后得到一组数据如下．由上表可得线性回归方程，则（ ）
A． B． C． D．
【答案】B
【解析】由表格数据知，．即样本中心点为，
由，得，即，
所以，即，可得，故选：B．
【变式5-3】（2023·河北·统考模拟预测）随着全球新能源汽车市场蓬勃增长，在政策推动下，中国新能源汽车企业在10余年间实现了“弯道超车”，一跃成为新能源汽车产量连续7年居世界第一的全球新能源汽车强国．某新能源汽车企业基于领先技术的支持，改进并生产纯电动车、插电混合式电动车、氢燃料电池车三种车型，生产效益在短期内逐月攀升，该企业在1月份至6月份的生产利润y（单位，百万元）关于月份的数据如下表所示，并根据数据绘制了如图所示的散点图．
（1）根据散点图判断，与（，，，d均为常数）哪一个更适宜作为利润关于月份的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的结果及表中的数据，求出y关于的回归方程；
（3）该车企为提高新能源汽车的安全性，近期配合中国汽车技术研究中心进行了包括跌落、追尾、多车碰撞等一系列安全试验项目，其中在实验场进行了一项甲、乙、丙三车同时去碰撞实验车的多车碰撞实验，测得实验车报废的概率为0.188，并且当只有一车碰撞实验车发生，实验车报废的概率为0.1，当有两车碰撞实验车发生，实验车报废的概率为0.2，由于各种因素，实验中甲乙丙三车碰撞实验车发生概率分别为0.7，0.5，0.4，且互不影响，求当三车同时碰撞实验车发生时实验车报废的概率．
参考数据：
其中，设，．
参考公式：对于一组具有线性相关关系的数据，其回归直线的斜率和截距的最小二乘估计公式分别为，．
【答案】（1）选用作为利润关于月份的回归方程更合适；
（2）；（3）
【解析】（1）散点图中的点的分布不是一条直线，相邻两点在轴上的差距是增大的趋势．
故选用作为利润关于月份的回归方程更合适．
（2）由，取对数可得，设，所以，
，，，，
所以，
，所以，
，即．
（3）设事件为“实验车报废”，事件为“只有一车碰撞实验车”，
事件为“恰有两车碰撞实验车”，事件为“三车碰撞实验车”，
则
由已知得，
利用全概率公式得
解得
所以当三车同时碰撞实验车发生时实验车报废的概率为0.5．
题型六 独立检验性的概念理解
【例6】（2023·全国·高二专题练习）为了探究电离辐射的剂量与人体的受损程度是否有关，用两种不同剂量的电离辐射照射小白鼠（可用小白鼠模拟人体受损程度）．在照射后14天内的结果如表所示：
进行统计分析时的统计假设是______．
【答案】电离辐射的剂量与人体受损程度无关
【解析】根据独立性检验知，应假设“电离辐射的剂量与人体受损程度无关”．
【变式6-1】（2023·陕西榆林·统考三模）若由一个列联表中的数据计算得，则（ ）
A．能有的把握认为这两个变量有关系
B．能有的把握认为这两个变量没有关系
C．能有的把握认为这两个变量有关系
D．能有的把握认为这两个变量没有关系
【答案】A
【解析】因为，所以能有的把握认为这两个变量有关系．故选：A
【变式6-2】（2022·四川南充·高三统考期中）当前新冠病毒仍然肆虐，已经成为全球性威胁．为了检测某种新冠病毒疫苗的效果，现随机抽取100只小白鼠进行试验，得到如下2×2列联表：则下列说法一定正确的是（ ）
附：（其中）．临界值表：
A．有99.5%的把握认为“小白鼠有无被感染与是否注射疫苗有关”
B．有99.5%的把握认为“小白鼠有无被感染与是否注射疫苗无关”
C．在犯错误的概率不超过0.005的前提下，认为“小白鼠有无被感染与是否注射疫苗无关”
D．在犯错误的概率不超过0.05的前提下，认为“小白鼠有无被感染与是否注射疫苗有关”
【答案】D
【解析】根据 列联表， ，
，
所以有 的把握认为“小白鼠有无感染与是否注射疫苗有关”，
故选项A，B，C错误，D正确；故选：D.
【变式6-3】（2023春·河南南阳·高二校联考期中）已知两个分类变量X，Y的可能取值分别为和，通过随机调查得到样本数据，再整理成如下的2×2列联表：
若样本容量为75，且，则当判断X与Y有关系的把握最小时，a的值为（ ）
A．5 B．10 C．15 D．17
【答案】C
【解析】在两个分类变量的列联表中，当的值越小时，
认为两个分类变量有关的可能性越小.
令，得，
又样本容量为75，
，则，
，化简得，解得：，，
又，.故选：C.
题型七 独立性检验的综合应用
【例7】（2023春·湖南·高二校联考期中）甲、乙两地到某高校实施“优才计划”，即通过笔试，面试，模拟技能这3项考核程序后直接签约一批优秀毕业生，已知3项程序分别由3个考核组独立依次考核，当3项考核程序均通过后即可签约．2022年，该校数学系100名毕业生参加甲地“优才计划”的具体情况如下表（不存在通过3项程序考核放弃签约的情况）：
今年，该校数学系毕业生小明准备参加两地的“优才计划”，假定他参加各程序的结果相互不影响，且他的辅导员作出较客观的估计：小明通过甲地的每项程序的概率均为，通过乙地的各项程序的概率依次为，，．
（1）依据小概率值的独立性检验，判断这100名毕业生去年参加甲地“优才计划”能否签约与性别是否有关联？
（2）若小明通过甲、乙两地的程序的项数分别记为X，Y，分别求出X与Y的数学期望．
参考公式与临界值表：，．
【答案】（1）认为这100名毕业生去年参加甲地“优才计划”能否签约与性别无关
（2），
【解析】（1）列联表：
，
根据小概率值的独立性检验，
可认为这100名毕业生去年参加甲地“优才计划”能否签约与性别无关；
（2）由已知，小明通过甲地的每项程序的概率均为，
所以X服从二项分布，即，∴，
由题意：Y的可能取值为0，1，2，3，
，，
，．
所以Y的数学期望．
【变式7-1】（2023春·辽宁大连·高二大连二十四中校考期中）在年春节期间，为了进一步发挥电子商务在活跃消费市场方面的积极作用，保障人民群众度过一个平安健康快乐祥和的新春佳节，甲公司和乙公司在某购物平台上同时开启了打折促销、直播带年货活动，甲公司和乙公司所售商品类似，存在竞争关系．
（1）现对某时间段名观看直播后选择这两个公司直播间购物的情况进行调查，得到如下数据：
请将表格补充完整，并判断是否有的把握认为选择哪家直播间购物与用户的年龄有关？
（2）若小李连续两天每天选择在甲、乙其中一个直播间进行购物，第一天等可能地从甲、乙两家中选一家直播间购物，如果第一天去甲直播间购物，那么第二天去甲直播间购物的概率为；如果第一天去乙直播间购物，那么第二天去甲直播间购物的概率为，求小李第二天去乙直播间购物的概率．
参考公式：，其中．
临界值表：
【答案】（1）列联表见解析，有，理由见解析；（2）
【解析】（1）列联表如下：
所以，，
所以，有的把握认为选择哪家直播间购物与用户的年龄有关.
（2）记事件小李第一天去甲直播间，事件小李第二天去乙直播间，
则，，，
由全概率公式可得.
因此，小李第二天去乙直播间购物的概率为.
【变式7-2】（2023·浙江金华·统考模拟预测）某市阅读研究小组为了解该城市中学生阅读与语文成绩的关系，在参加市中学生语文综合能力竞赛的各校学生中随机抽取了500人进行调查，并按学生成绩是否高于75分（满分100分）及周平均阅读时间是否少于10小时，将调查结果整理成列联表.现统计出成绩不低于75分的样本占样本总数的，周平均阅读时间少于10小时的人数占样本总数的一半，而不低于75分且周平均阅读时间不少于10小时的样本有100人.
（1）根据所给数据，求出表格中和的值，并分析能否有以上的把握认为语文成绩与阅读时间是否有关；
（2）先从成绩不低于75分的样本中按周平均阅读时间是否少于10小时分层抽样抽取9人进一步做问卷调查，然后从这9人中再随机抽取3人进行访谈，记抽取3人中周平均阅读时间不少于10小时的人数为，求的分布列与均值.
参考公式及数据：.
【答案】（1），有的把握认为语文成绩与阅读时间有关
（2）分布列见解析，数学期望为
【解析】（1）根据已知条件，列联表如下：
所以，由表知，
所以有的把握认为语文成绩与阅读时间有关.
（2）依题意，成绩不低于75分的学生中周平均阅读时间少于10小时和
不少于10小时的人数比是1:2，
按分层抽样抽取9人，则周平均阅读时间少于10小时有3人，
不少于10小时的有6人，
从这9人中再随机抽取3人进行访谈，则可能的取值为，
，.
分布列如下：
.
【变式7-3】（2023·全国·高三专题练习）2022年4月21日，国务院办公厅印发《关于推动个人养老金发展的意见》，明确参加人每年缴纳个人养老金的上限为12000元，10月26日，人力资源社会保障部、财政部、国家税务总局、银保监会、证监会联合发布《个人养老金实施办法》．某高校一社团就是否愿意缴纳个人养老金的情况随机采访了200位市民，并将结果进行了统计，得到如下列联表．
（1）根据上面的列联表，依据的独立性检验，能否认为对缴纳个人养老金的态度与性别有关?
（2）为了进一步了解公民对缴纳个人养老金的意见和建议，从抽取的200位市民中对不愿意缴纳个人养老金的公民按照分层抽样的方法抽取6人，再从这6人中随机抽取3人进行电话回访，求3人中至少有1人为男性的概率．
附：，其中．
【答案】（1）能认为对缴纳个人养老金的态度与性别有关；（2）0.8
【解析】（1）零假设为：对缴纳个人养老金的态度与性别无关．
由列联表中的数据可得．
所以依据的独立性检验，没有充分证据推断成立，
因此可以认为不成立，
即能认为对缴纳个人养老金的态度与性别有关．
（2）设按分层抽样的方法，应从不愿意缴纳个人养老金的男性中抽取x人，
从不愿意缴纳个人养老金的女性中抽取y人，
由分层抽样的定义可知，得，．
则从这6人中抽取3人的所有基本情况共有（种），
其中至少有1人为男性的情况有（种）．
记事件A为“3人中至少有1人为男性”，则，
故所求概率为0.8．年份
2011
2012
2013
2014
2015
2016
2017
2018
2019
2020
2021
数学x（分）
75
77
79
74
80
81
77
83
80
82
81
英语m（分）
95
98
100
101
102
103
101
98
107
106
100
总分y（分）
473
481
479
485
490
487
478
492
488
493
489
15
16
18
19
22
102
98
115
115
120
（次/分钟）
24
36
40
60
（℃）
26
28.6
30
35.4
气温x
18
13
10
用电量y
24
34
38
64
1
2
3
4
5
2.4
2.7
4.1
6.4
7.9
1
2
3
4
5
232
98
60
40
20
1
2
3
年份（年）
2018
2019
2020
2021
2022
年销售量y（单位：万辆）
9
16.5
29
46.5
69
34
55
979
660
2805
x
1
2
3
4
5
z
2
4
5
10
14
月份
1
2
3
4
5
6
收入（百万元）
6.8
8.6
16.1
19.6
28.1
40.0
19.87
2.80
17.50
113.75
6.30
死亡
存活
合计
第一种剂量
14
11
25
第二种剂量
6
19
25
合计
20
30
50
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
感染
未感染
总计
注射
10
40
50
未注射
20
30
50
总计
30
70
100
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
10
a
b
30
人数性别
参加考核但未能签约的人数
参加考核并能签约的人数
男生
35
15
女生
40
10
0.10
0.05
0.010
2.706
3.841
6.635
人数性别
参加考核但未能签约的人数
参加考核并能签约的人数
合计
男生
35
15
50
女生
40
10
50
合计
75
25
100
选择甲公司直播间购物
选择乙公司直播间购物
合计
用户年龄段岁
用户年龄段岁
合计
选择甲公司直播间购物
选择乙公司直播间购物
合计
用户年龄段岁
用户年龄段岁
合计
周平均阅读时间少于10小时
周平均阅读时间不少于10小时
合计
75分以下
不低于75分
100
合计
500
0.01
0.005
0.001
6.635
7.879
10.828
周平均阅读时间少于10小时
周平均阅读时间不少于10小时
合计
75分以下
200
150
350
不低于75分
50
100
150
合计
250
250
500
0
1
2
3
愿意缴纳
不愿意缴纳
合计
男性
80
20
100
女性
60
40
100
合计
140
60
200
α
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828