第3章 圆的基本性质复习 浙教版数学九年级上册课件

这是一份第3章 圆的基本性质复习 浙教版数学九年级上册课件，共20页。

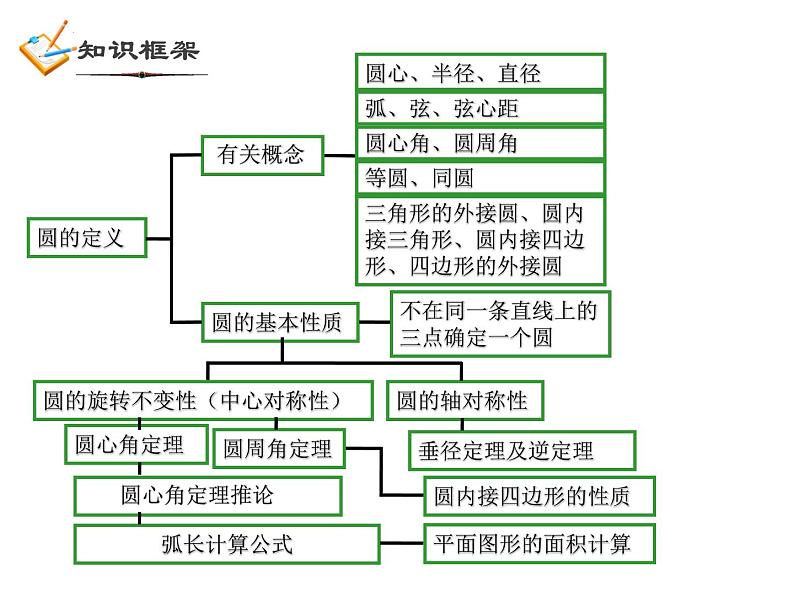
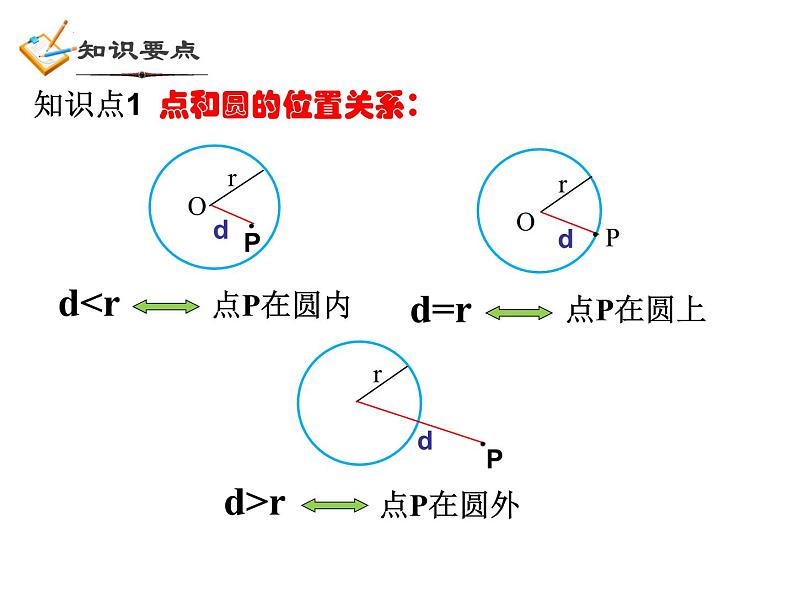
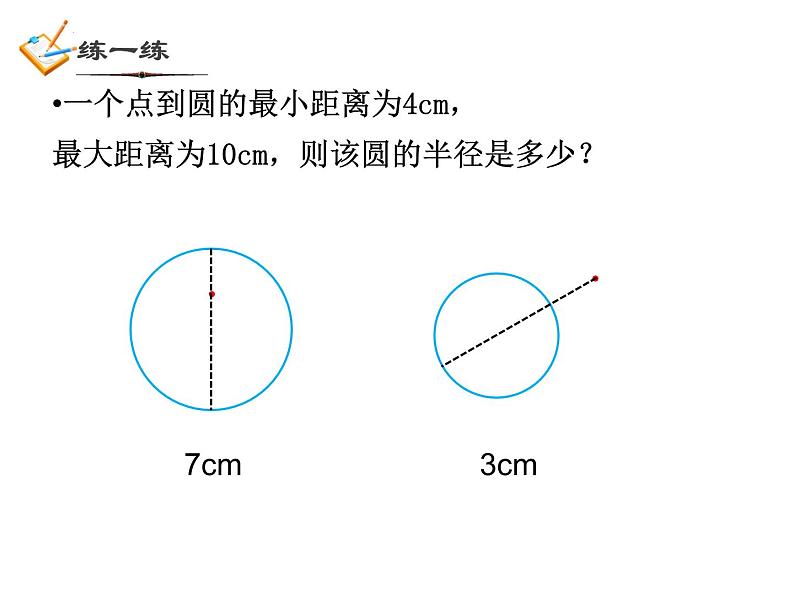
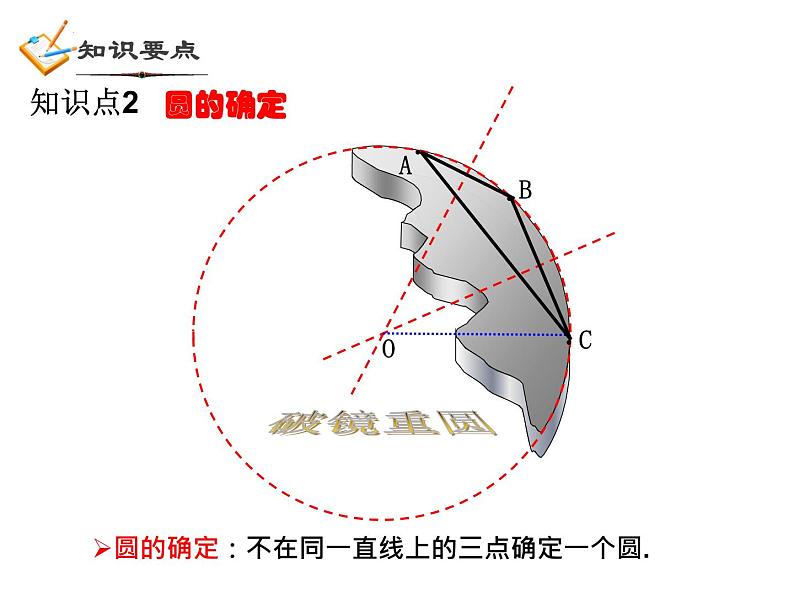
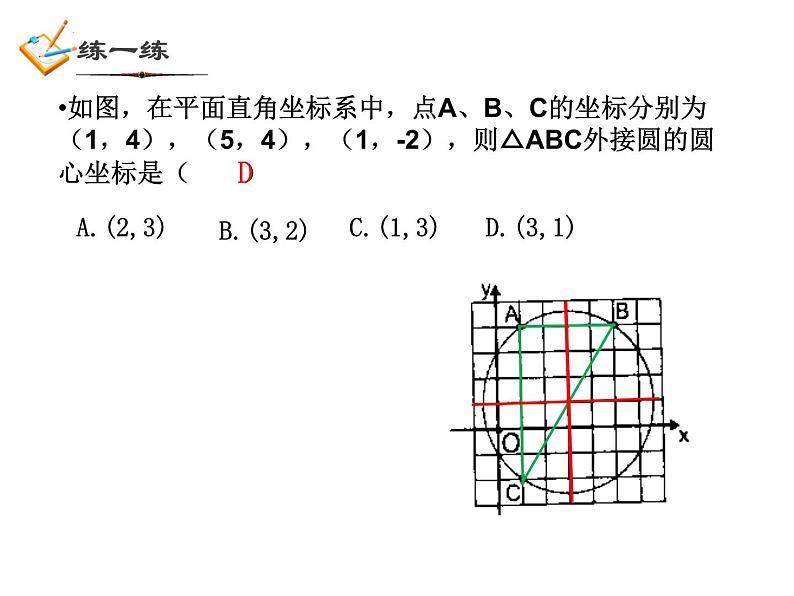
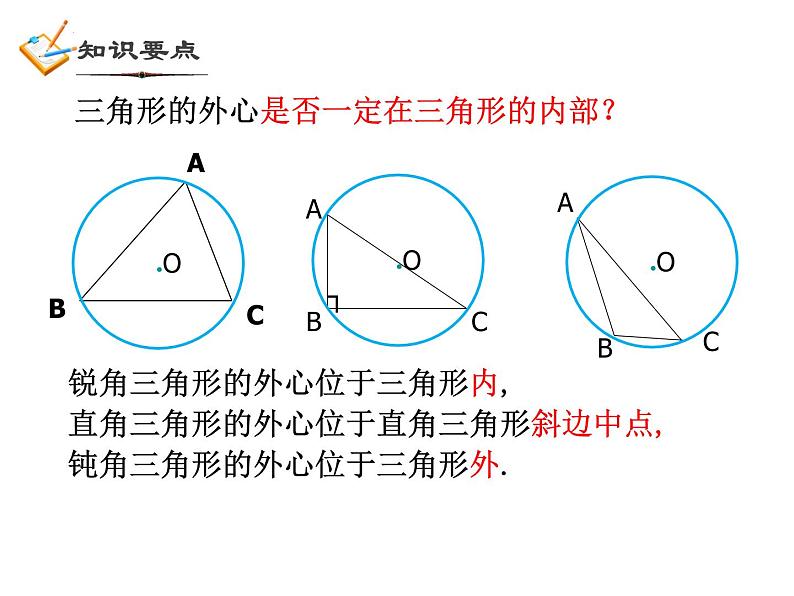
第3章 圆的基本性质复习三角形的外接圆、圆内接三角形、圆内接四边形、四边形的外接圆圆的定义 有关概念圆的旋转不变性（中心对称性）圆心、半径、直径圆心角定理不在同一条直线上的三点确定一个圆弧长计算公式圆的基本性质弧、弦、弦心距圆心角、圆周角等圆、同圆 圆心角定理推论圆的轴对称性圆周角定理垂径定理及逆定理圆内接四边形的性质 平面图形的面积计算点和圆的位置关系：知识点1一个点到圆的最小距离为4cm，最大距离为10cm，则该圆的半径是多少？7cm3cm圆的确定：不在同一直线上的三点确定一个圆.圆的确定O破镜重圆知识点2如图，在平面直角坐标系中，点A、B、C的坐标分别为（1，4），（5，4），（1，-2），则△ABC外接圆的圆心坐标是（ ）DA.(2,3)B.(3,2)C.(1,3)D.(3,1)锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.三角形的外心是否一定在三角形的内部？1.过一点的圆有________个2.过两点的圆有_________个，这些圆的 圆心的都在 上.3.过三点的圆有________个4.如何作过不在同一直线上的三点的圆（或三角形的外接圆、找外心、破镜重圆、 到三个村庄距离相等）无数无数0或1连结两点线段的垂直平分线圆的轴对称性EDBA垂径定理：AB是直径 AB CD于E推论: （2）平分弦所对的一条弧的直径， 垂直平分弦并且平分弦所对的另一条弧（1）平分弦 的直径 垂直于弦，并且平分弦所对的两条弧；（不是直径）（3）弦的垂直平分线一定经过圆心，并平分 弦所对的另一条弧（4）平行弦所夹的弧相等知识点3如图,已知⊙O的半径OA长为5,弦AB的长8,OC⊥AB于C,则OC的长为 _______.3AC=BC如图，P为⊙O的弦BA延长线上一点，PA＝AB＝8，PO＝13，则⊙O的半径＝＿＿＿.圆中跟弦有关的计算问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线. 圆心到弦的距离(弦心距)、半径、一半弦长构成直角三角形，便将问题转化为直角三角形的问题.Ａ圆的旋转不变性知识点4圆心角、弧、弦、弦心距之间的关系如图,在同圆中,OC⊥AB于C,OC′⊥A′ B′于C′. ∵ ， ∴ AB = A′ B′ （填写一个条件．你有几种填法？你的根据是什么？） 　　　　　如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等.在同圆或等圆中：⑴圆周角 与圆心角如图：⑴ 如果∠AOB=100°，则∠C= .ABCO⑵ 当∠C= 时，A、O、B三点在同一直线上.　　　　　圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.　　　　　推论：半圆（或直径）所对的圆周角是直角；90°的圆周角所对弦是直径. 50°90°120° 125°如图，比较∠C、∠D、∠E的大小同弧所对的圆周角相等如图，如果弧AB＝弧CD，那么∠E和∠F是什么关系？反过来呢？等弧所对的圆周角相等；在同圆中，相等的圆周角所对的弧也相等如图，⊙O1和⊙O2是等圆，如果弧AB＝弧CD，那么∠E和∠F是什么关系？反过来呢？等圆也成立⑵圆周角与弧例 如图,⊙O 中，弦AB=CD，AB 与CD交于点M，BCADMO∠AOB=______ 度，已知：如图，△ABC内接于⊙O ，点A、B、C把⊙O三等分，则 弧AB=______ 度 ，∠ ACB=______ 度注意: 弧的度数和角的度数的相互转化120°120°60°m 如图,已知AB是⊙O的直径,AB与弦CD相交于 点M,∠AMC=300 ,AM=6cm，MB=2cm,求CD的长.N圆及其有关概念；点与圆的位置关系；确定一个圆的条件；圆的轴对称性；中心对称性；圆在旋转变换中的特有性质.圆的性质：