初中4.5 相似三角形的性质及应用课后练习题

这是一份初中4.5 相似三角形的性质及应用课后练习题，共11页。试卷主要包含了5米,等内容，欢迎下载使用。
基础过关全练
知识点 相似三角形性质的实际应用
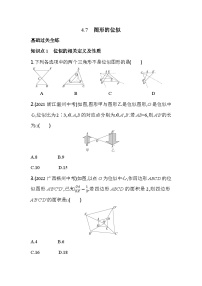
1.(2023浙江金华义乌月考)如图,小明在A时测得某树的影长为3 m,B时又测得该树的影长为2 m,若两次日照的光线互相垂直,则树的高度为 m.( )( )
A.6-6 B.6 C.6 D.5
2.(2021河北中考)图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时AB=( )( )
A.1 cm B.2 cm
C.3 cm D.4 cm
3.【数学文化】(2022广西北部湾经济区中考)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是 米.
4.在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量,如图,若a1=1米,a2=10米,h=1.8米,则这个学校教学楼的高度为 米.( )
5.【教材变式·P147例6】(2022陕西中考)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一条直线上,A、B、O三点在同一条直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
能力提升全练
6.(2023浙江温州洞头期中,10,★★☆)在一次实验操作中,图①是一个长和宽均为3,高为8的长方体容器,将其放置在水平桌面上,里面盛有水,水面高为6.现将图①所示的容器向右倾倒,按如图②所示的方式放置,发现此时水面恰好触到容器口边缘,则图②中水面高度为( )( )

图① 图②
A.245 B.325
C.123417 D.203417
7.(2020浙江温州中考,16,★★★)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一条直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为 米,BC为 米.( )
8.有一块锐角三角形卡纸余料ABC,它的边BC=120 cm,高AD=80 cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边FG在BC上,正方形纸片一边在矩形纸片的较长边EH上,其余顶点分别在AB,AC上,具体裁剪方式如图所示.
(1)求矩形纸片的较长边EH的长;
(2)裁剪正方形纸片时,小聪是按以下方法进行裁剪的:先沿着余料△AEH中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线段剪两刀,请你通过计算,判断小聪的剪法是否正确.
素养探究全练
9.【推理能力】(2023浙江温州瑞安月考)下图是某路灯的示意图,立柱OE与水平地面垂直,两盏路灯挂在灯杆OE的两侧,灯臂AB,CD近似看成线段,AB=CD,AE⊥OE,∠ABO=∠DCO=120°.小丽(身高1.5米)站在点P处时,点F,D,E在同一条直线上,向后移动4.5米到达点Q,此时点G,D,B,A在同一条直线上,测得OP=6米,求灯杆OE及灯臂AB的长.
答案全解全析
基础过关全练
1.B 根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2 m,FD=3 m,
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又∵∠CDE=∠FDC=90°,∴△EDC∽△CDF,
∴EDDC=DCFD,即DC2=ED·FD=2×3=6,
∴CD=6 m.故选B.
2.C 如图,过O作OM⊥CD,垂足为M,过O'作O'N⊥AB,垂足为N,
由题意得△CDO∽△ABO',∴CDAB=OMO'N,
∵OM=15-7=8 cm,O'N=11-7=4 cm,
∴6AB=84,∴AB=3 cm,故选C.
3.答案 134
解析 设金字塔的高度BO为x米,根据相同时刻的物高与影长成比例,可得4268=2x,解得x=134,
经检验,x=134是原方程的解,且符合题意,
∴金字塔的高度BO是134米.
4.答案 18
解析 如图,由镜面反射原理可得∠1=∠2,
∵∠ACB=∠ADE=90°,∴△ACB∽△ADE,
∴ACAD=CBDE,∴110=1.8DE,∴ED=18米,
即这个学校教学楼的高度为18米.
5.解析 ∵AD∥EG,∴∠ADO=∠EGF,
∵∠AOD=∠EFG=90°,∴△AOD∽△EFG,
∴AOEF=ODFG,即AO1.8=202.4,
∴AO=15米,
同理得△BOC∽△AOD,
∴BOAO=OCOD,即BO15=1620,
∴BO=12米,
∴AB=AO-BO=15-12=3(米).
能力提升全练
6.A 过点C作CF⊥BG于F,如图所示:
设DE=x,则AD=8-x,
根据题意得12(8-x+8)×3×3=3×3×6,
解得x=4,∴DE=4,
∵∠E=90°,
∴由勾股定理得CD=DE2+CE2=42+32=5,
∵∠BCE=∠DCF=90°,∴∠DCE=∠BCF,
又∵∠DEC=∠BFC=90°,∴△CDE∽△CBF,
又∴CECF=CDCB,即3CF=58,∴CF=245,
故选A.
7.答案 152;202
解析 ∵AE⊥l,BF⊥l,∠ANE=45°,
∴△ANE和△BNF都是等腰直角三角形,
∴AE=EN,BF=FN,
∵EF=15米,FM=2米,MN=8米,
∴AE=EN=15+2+8=25(米),BF=FN=2+8=10(米),
∴AN=252 米,BN=102 米,∴AB=AN-BN=152 米.
如图,过C作CH⊥l于H,过B作PQ∥l交AE于P,交CH于Q,
∴AE∥CH,
∴四边形PEHQ、四边形PEFB和四边形BFHQ都是矩形,
∴PE=BF=QH=10米,PB=EF=15米,BQ=FH,
∵∠1=∠2,∠AEF=∠CHM=90°,∴△AEF∽△CHM,
∴CHAE=HMEF,∴CHHM=AEEF=2515=53,
设HM=3x米,CH=5x米,x>0,
∴CQ=(5x-10)米,BQ=FH=(3x+2)米,
∵∠APB=∠ABC=∠CQB=90°,
∴∠ABP+∠PAB=∠ABP+∠CBQ=90°,
∴∠PAB=∠CBQ,∴△APB∽△BQC,
∴APBQ=PBCQ,又易知PA=PB=15米,
∴153x+2=155x-10,解得x=6,
∴BQ=CQ=20米,∴BC=202米.
故答案为152;202.
8.解析 (1)设EF=2x cm,EH=5x cm,x>0,
则AR=(80-2x)cm.
∵四边形EFGH为矩形,∴EH∥BC,
∴△AEH∽△ABC,∴EHBC=ARAD,即5x120=80-2x80,
解得x=15,∴EH=15×5=75(cm),
∴矩形纸片较长边EH的长为75 cm.
(2)小聪的剪法不正确.
理由如下:设正方形的边长为a cm,则PQ=KR=a cm,
由(1)可知AR=80-2×15=50(cm),
∴AK=(50-a)cm,由题意可知△APQ∽△AEH,
∴PQEH=AKAR,即a75=50-a50,解得a=30,∴PQ=30 cm.
∵与边EH平行的中位线的长为12×75=37.5 cm,37.5≠30,
∴小聪的剪法不正确.
素养探究全练
9.解析 如图,过点G作GH⊥EO于点H,则G,F,H在同一条直线上,
∴四边形HFPO,四边形FGQP,四边形HGQO都是矩形,
∴HF=OP=6米,FG=PQ=4.5米,OH=FP=GQ=1.5米,
∴HG=HF+FG=10.5米,
∵∠ABO=∠DCO=120°,
∴∠CBD=∠BCD=60°,
∴△BCD是等边三角形,∴BC=BD=DC,
∵AB=CD,∴BC=BD=DC=AB,
∵AE⊥OE,∠ABE=60°,∴∠A=30°,
设BE=x米,则AB=BC=BD=DC=2x米,
∴AE=3x米,
∵GH⊥OE,∴AE∥GH,
∴∠BGH=∠A=30°,∴BG=2BH,
∵BH2+HG2=BG2,
∴BH2+10.52=4BH2,∴BH=732米,
∴BG=2BH=73米,
∴DG=BG-DB=(73-2x)米,
∵AE∥FG,∴△AED∽△GFD,
∴AEFG=ADDG,∴3x4.5=4x73-2x,
∴x=32或x=0(舍去),∴BE=32米,AB=3米,
∴OE=OH+BH+BE=1.5+732+32=(1.5+43)米.