2023-2024学年辽宁省盘锦市辽河油田实验中学九年级（上）期中数学试卷（含解析）

这是一份2023-2024学年辽宁省盘锦市辽河油田实验中学九年级（上）期中数学试卷（含解析），共28页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列事件中，是必然事件的是( )
A. 任意画一个三角形，其内角和是180°B. 任意买一张电影票，座位号是单号
C. 掷一次骰子，向上一面的点数是3D. 射击运动员射击一次，命中靶心
2.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据，可得y关于x的函数表达式为( )
A. y=100xB. y=x100C. y=400xD. y=x400
3.已知反比例函数y=1x，下列结论不正确的是( )
A. 图象经过点(1,1)B. 图象在第一、三象限
C. 当x>1时，04.若点A(x1,−2)，B(x2,1)，C(x3,2)都在反比例函数y=−2x的图象上，则x1，x2，x3的大小关系是( )
A. x35.甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是( )
A. 掷一枚正六面体的骰子，出现1点的概率
B. 抛一枚硬币，出现正面的概率
C. 任意写一个整数，它能被3整除的概率
D. 从一个装有2个白球和1个红球的袋子中任取一球，取到白球的概率
6.如图，点P在△ABC的边AC上，要判断△ABP≌△ACB，添加下列一个条件，不正确的是( )
A. ∠ABP=∠C
B. ∠APB=∠ABC
C. APAB=BPBC
D. APAB=ABAC
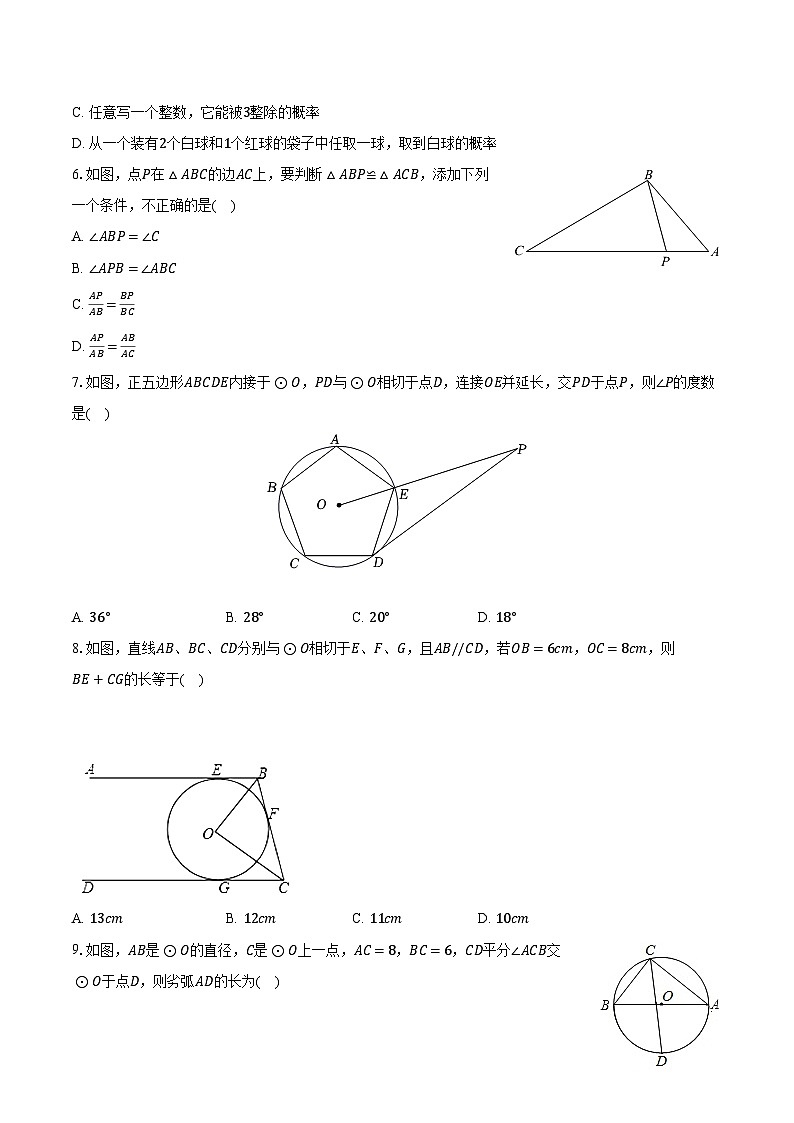
7.如图，正五边形ABCDE内接于⊙O，PD与⊙O相切于点D，连接OE并延长，交PD于点P，则∠P的度数是( )
A. 36°B. 28°C. 20°D. 18°
8.如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB/​/CD，若OB=6cm，OC=8cm，则BE+CG的长等于( )
A. 13cmB. 12cmC. 11cmD. 10cm
9.如图，AB是⊙O的直径，C是⊙O上一点，AC=8，BC=6，CD平分∠ACB交⊙O于点D，则劣弧AD的长为( )
A. π
B. 32π
C. 2π
D. 52π
10.如图，在△ABC中，AB=AC，∠A=36°.以点B为圆心，适当长为半径作圆弧，交AB于点M，交BC于点N.接着分别以点M，N为圆心，大于12MN长为半径作圆弧，两弧交于点H.作射线BH，交AC于点D.再以点D为圆心，DC长为半径作圆弧，交BC于点E，连结DE.则下列说法错误的是( )
A. AD=BD
B. ∠BDC=∠BCD
C. AD= 3BE
D. △BED∽△BDA
二、填空题：本题共6小题，每小题3分，共18分。
11.如图，点A是反比例函数y=kx(x<0)的图象上的一点，点B在x轴的负半轴上且AO=AB，若△ABO的面积为4，则k的值为______．
12.如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=2.以点C为圆心，CB长为半径画弧，分别交AC，AB于点D，E，则图中阴影部分的面积为 (结果保留π)．
13.如图，将△ABC的AB边与刻度尺的边缘重合，点A，D，B分别对应刻度尺上的整数刻度.已知DE/​/AC，EF/​/AB，AF=1.8cm，则CF= ______ ．
14.如图，在边长为1的方格纸中，点A，B，C，D都在方格纸的交点处，线段AB与CD相交于点E，△ADE∽△BCE，则AEBE的值为______．
15.如图，在平面直角坐标系中，菱形ABCD的边BC与x轴平行，A，B两点纵坐标分别为4，2，反比例函数y=kx经过A，B两点，若菱形ABCD面积为8，则k值为______．
16.矩形纸片ABCD中，AB=3，BC=5，点M在AD边所在的直线上，且DM=1，将矩形纸片ABCD折叠，使点B与点M重合，折痕与AD，BC分别交于点E，F，则线段EF的长度为______ ．
三、计算题：本大题共1小题，共8分。
17.如图，AB是圆O的直径，CD是圆O的一条弦，且CD⊥AB于点E．
(1)若∠A=48°，求∠OCE的度数；
(2)若CD=4 2，AE=2，求圆O的半径．
四、解答题：本题共7小题，共74分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
为了调动同学们学习数学的积极性，班内组织开展了“数学小先生”讲题比赛，老师将四道备讲题的题号1，2，3，4，分别写在完全相同的4张卡片的正面，将卡片背面朝上洗匀．
(1)随机抽取一张卡片，卡片上的数字是“4”的概率是______；
(2)小明随机抽取两张卡片，用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率．
19.(本小题8分)
如图，AO=4cm，AB=5cm，DO=9cm，BC=12cm，O为BC的中点，求△CDO的周长．
20.(本小题10分)
如图，在平面直角坐标系中，直线y=2x+4与x轴、y轴分别相交于点A、点B，连接AB，以AB为边长作正方形ABCD．
(1)求正方形ABCD的面积；
(2)求点D的坐标；
(3)若曲线y=kx在第二象限经过点D，过点C作CF⊥y轴于点F，交曲线于点E，求EF的长．
21.(本小题12分)
如图，以四边形ABCD的对角线BD为直径作圆，圆心为O，过点A作AE⊥CD的延长线于点E，已知DA平分∠BDE．
(1)求证：AE是⊙O切线；
(2)若AE=4，CD=6，求⊙O的半径和AD的长．
22.(本小题12分)
如图，已知一次函数y=kx+6的图象与反比例函数y=mx(m>0)的图象交于A(3,4)，B两点，与x轴交于点C，将直线AB沿y轴向上平移3个单位长度后与反比例函数图象交于点D，E．
(1)求k，m的值及C点坐标；
(2)根据图象直接写出不等式kx+6>mx的解集；
(3)连接AD，CD，求△ACD的面积．
23.(本小题12分)
如图，在△ABC中，AB=AC，以AB为直径的⊙O交边AC于点D(点D不与点A重合)，交边BC于点E，过点E作EF⊥AC，垂足为F．
(1)求证：EF是⊙O的切线；
(2)连接DE，求证：△DEC是等腰三角形；
(3)若CD=2，BE=3，求⊙O的半径．
24.(本小题12分)
如图，D是等腰三角形ABC底边的中点，过点A、B、D作⊙O．
(1)求证：AB是⊙O的直径；
(2)延长CB交⊙O于点E，连接DE，求证：DC=DE；
(3)若BC=5，CD=4，求BE长．
答案和解析
1.【答案】A
【解析】解：A、任意画一个三角形，其内角和是180°，是必然事件，故A不符合题意；
B、任意买一张电影票，座位号是单号，是随机事件，故B符合题意；
C、掷一次骰子，向上一面的点数是3，是随机事件，故C不符合题意；
D、射击运动员射击一次，命中靶心，是随机事件，故D不符合题意；
故选：A．
根据随机事件，必然事件，不可能事件的特点，逐一判断即可解答．
本题考查了随机事件，三角形的内角和定理，熟练掌握随机事件，必然事件，不可能事件的特点是解题的关键．
2.【答案】A
【解析】解：由表格中数据可得：xy=100，
故y关于x的函数表达式为：y=100x．
故选：A．
直接利用已知数据可得xy=100，进而得出答案．
此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．
3.【答案】D
【解析】解：A：k=1×1=1，∴不符合题意；
B：∵k>0，∴图象在第一、三象限，∴不符合题意；
C：当x>1时，0D：∵k>0，∴在每一象限内y随x的增大而增大，∴符合题意；
故选：D．
A：根据k=xy计算；
B：根据性质k>0判断函数图像经过的象限；
C：∵x=1时，y=1，当x>1时，求出y的取值范围；
D：在每一象限内y随x的增大而增大．
本题考查反比例函数的性质，熟练掌握反比例函数根据性质判断经过的象限、递增情况和y的取值范围，根据x的取值范围求y的取值范围是本题难点．
4.【答案】D
【解析】解：将A(x1,−2)代入y=−2x，得：−2=−2x1，即：x1=1，
将B(x2,1)代入y=−2x，得：1=−2x2，即：x2=−2，
将C(x3,2)代入y=−2x，得：2=−2x3，即：x3=−1，
∴x2故选：D．
分别将点A，B，C的坐标代入反比例函数的解析式求出x2，x3，x1，然后再比较它们的大小即可得出答案．
此题主要考查了反比例函数的图象，解答此题的关键是理解函数图象上的点满足函数的解析式，满足函数解析式的点都在函数的图象上．
5.【答案】C
【解析】解：A、掷一枚正六面体的骰子，出现1点的概率为16，故此选项不符合题意；
B、掷一枚硬币，出现正面朝上的概率为12，故此选项不符合题意；
C、任意写一个整数，它能被3整除的概率为13≈0.33，故此选项符合题意；
D、从一个装有2个白球和1个红球的袋子中任取一球，取到白球的概率为22+1≈0.67，故此选项不符合题意．
故选：C．
根据统计图可知，试验结果在0.33附近波动，即其概率P≈0.33，计算四个选项的概率，约为0.33者即为正确答案．
本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．同时此题在解答中要用到概率公式．
6.【答案】C
【解析】解：在△ABP和△ACB中，∠BAP=∠CAB，
∴当∠ABP=∠C时，满足两组角对应相等，可判断△ABP∽△ACB，故A正确；
当∠APB=∠ABC时，满足两组角对应相等，可判断△ABP∽△ACB，故B正确；
当APAB=BPBC时，其夹角不相等，则不能判断△ABP∽△ACB，故C不正确；
当APAB=ABAC时，满足两边对应成比例且夹角相等，可判断△ABP∽△ACB，故D正确；
故选：C．
根据相似三角形的判定方法，逐项判断即可．
本题主要考查相似三角形的判定，掌握相似三角形的判定方法是解题的关键，即在两个三角形中，满足三边对应成比例、两边对应成比例且夹角相等或两组角对应相等，则这两个三角形相似．
7.【答案】D
【解析】解：如图，连接OD．
∵PD是⊙O的切线，
∴∠ODP=90°，
∵五边形ABCDE是正五边形，
∴∠EOD=360°5=72°，
∴∠P=90°−∠POD=18°．
故选：D．
连接OD，利用切线的性质证明∠ODP=90°，再利用正五边形的性质求出∠POD，可得结论．
本题考查正多边形与圆，切线的性质等知识，解题的关键是熟练掌握正五边形的性质，切线的性质，属于中考常考题型．
8.【答案】D
【解析】【分析】
此题主要是考查了切线长定理.从圆外一点引圆的两条切线，它们的切线长相等，且圆心和这点的连线平分两条切线的夹角．
根据平行线的性质以及切线长定理，即可证明∠BOC=90°，再根据勾股定理即可求得BC的长，再结合切线长定理即可求解．
【解答】
解：∵AB/​/CD，
∴∠ABC+∠BCD=180°，
∵CD、BC，AB分别与⊙O相切于G、F、E，
∴∠OBC=12∠ABC，∠OCB=12∠BCD，BE=BF，CG=CF，
∴∠OBC+∠OCB=90°，
∴∠BOC=90°，
∴BC= OB2+OC2=10，
∴BE+CG=BF+CF=BC=10(cm)．
故选D．
9.【答案】D
【解析】解：连接OD，
∵AB是⊙O的直径，
∴∠ACB=90°，
在Rt△ABC中，AC=8，BC=6，由勾股定理得AB=10，
∴AO=5，
∵CD平分∠ACB，
∴∠ACD=12∠ACB=45°，
由圆周角定理得∠AOD=2∠ACD=90°，
∴劣弧AD的长为90π×5180=52π.
故选：D．
求得半径和弧所对的圆心角，利用弧长公式求解即可．
考查了弧长公式的应用，解题的关键是牢记弧长的计算公式，难度不大．
10.【答案】C
【解析】解：由作图得BD平分∠ABC，DE=DC，
∵AB=AC，∠A=36°，
∴∠ABC=∠ACB=180°−36°2=72°，
∴∠ABD=∠CBD=12∠ABC=12×72°=36°，
∴∠ABD=∠A，
∴AD=BD，
故A正确；
∵∠BDC=∠ABD+∠A=36°+36°=72°，∠BCD=72°，
∴∠BDC=∠BCD，
故B正确；
∵DE=DC，
∴∠DEC=∠DCE=72°，
∴∠EDB=∠DEC−∠CBD=72°−36°=36°，
∴∠EDB=∠CBD，
∴BE=DE=DC，
∵∠DBE=∠ABD=36°，∠EDB=∠A=36°，
∴△BED∽△BDA，
故D正确；
∴BDAB=DEAD，
∴ADAC=DCAD，
∴AD2=DC⋅AC，
设AD=x，BE=DC=m，则AC=x+m，
∴x2=m(x+m)，
解关于x的方程得x1=1+ 52m，x2=1− 52m(不符合题意，舍去)，
∴AD=1+ 52BE≠ 3BE，
故C错误，
故选：C．
由作图得BD平分∠ABC，DE=DC，由AB=AC，∠A=36°，得∠ABC=∠ACB=72°，则∠ABD=∠CBD=36°=∠A，所以AD=BD，可判断A正确；因为∠BDC=∠ABD+∠A=72°，∠BCD=72°，所以∠BDC=∠BCD，可判断B正确；因为∠DEC=∠DCE=72°，所以∠EDB=∠DEC−∠CBD=36°，则∠EDB=∠CBD，所以BE=DE=DC，由∠DBE=∠ABD=36°，∠EDB=∠A=36°，得△BED∽△BDA，可判断D正确；由BDAB=DEAD，得ADAC=DCAD，则AD2=DC⋅AC，可证明AD=1+ 52BE≠ 3BE，可判断C错误，于是得到问题的答案．
此题重点考查等腰三角形的判定与性质、三角形内角和定理、相似三角形的判定与性质、一元二次方程的解法等知识，证明△BED∽△BDA是解题的关键．
11.【答案】−4
【解析】解：过点A作AC⊥x轴，设点A(x,y)，
∵OA=AB，
∴OC=BC，
∴点B(2x,0)，
∵顶点A在反比例函数y=kx(x<0)的图象上，
∴xy=k，
∵△OAB的面积为4，
∴12OB⋅AC=4，
即12×2|x|×y=4，
∴xy=−4，
即k=−4．
故答案为：−4．
过点A作AC⊥x轴，设点A(x,y)，可得出xy=k，再根据三角形的面积公式即可得出答案．
本题考查了反比例函数系数k的几何意义以及等腰三角形的性质，反比例函数y=kx图象上的点(x,y)一定满足xy=k．
12.【答案】23π− 3
【解析】【分析】
连接CE，由扇形CBE面积−三角形CBE面积求解．本题考查扇形的面积与解直角三角形，解题关键是判断出三角形CBE为等边三角形与扇形面积的计算．
【解答】解：连接CE，
∵∠A=30°，
∴∠B=90°−∠A=60°，
∵CE=CB，
∴△CBE为等边三角形，
∴∠ECB=60°，BE=BC=2，
∴S扇形CBE=22×60π360=23π
∵S△BCE= 34BC2= 3，
∴阴影部分的面积为23π− 3．
故答案为：23π− 3．
13.【答案】1.2cm
【解析】解：由题意得，AD=4cm，AB=10cm，BD=6cm，
∵DE/​/AC，EF/​/AB，
∴四边形ADEF是平行四边形，
∴EF=AD=4cm，DE=AF=1.8cm，
∵DE/​/AC，
∴△BDE∽△BAC，
∴DEAC=BDAB，即1.81.8+CF=610，
解得CF=1.2，
经检验，CF=1.2是原方程的解，
∴CF=1.2cm，
故答案为：1.2cm．
先读数得到AD=4cm，AB=10cm，BD=6cm，再证明四边形ADEF是平行四边形，得到EF=AD=4cm，DE=AF=1.8cm，证明△BDE∽△BAC，利用相似三角形的性质得到1.81.8+CF=610，解方程即可得到答案．
本题主要考查了相似三角形的性质与判定，平行四边形的性质与判定，关键是平行线性质定理的应用．
14.【答案】12
【解析】解：由勾股定理得AD= 22+12= 5，
BC= 42+22=2 5，
∵△ADE∽△BCE，
∴AEBE=ADBC= 52 5=12，
故答案为：12．
先借助方格根据勾股定理求出AD，BC，再由相似三角形的性质求得结果．
本题主要考查了勾股定理，相似三角形的性质，熟练掌握相似三角形的性质是解题的关键．
15.【答案】−8 3
【解析】解：方法一：∵四边形ABCD是菱形，
∴AB=BC，AD//BC，
∵A、B两点的纵坐标分别是4、2，反比例函数y=kx经过A、B两点，
∴xB=k2，xA=k4，
即A(k4,4)，B(k2,2)，
∴AB2=(k4−k2)2+(4−2)2=k216+4，
∴BC=AB= k216+4，
又∵菱形ABCD的面积为8，
∴BC×(yA−yB)=8，
即 k216+4×(4−2)=8，
整理得 k216+4=4，
解得k=±8 3，
∵函数图象在第二象限，
∴k<0，即k=−8 3．
方法二：过点A作AE⊥BC于点E，
∵A、B两点的纵坐标分别是4、2，
∴AE=4−2=2，
∵菱形ABCD的面积为8，
∴BC⋅AE=8，
∴BC=4，
∴AB=BC=4，
∴BE=2 3，
设A点坐标为(a,4)，则B点的坐标为(a−2 3,2)，
∵反比例函数y=kx经过A、B两点，
∴ka=4ka−2 3=2,
解得k=−8 3a=−2 3,
故答案为−8 3．
方法一：根据函数解析式和A、B点的纵坐标，分别写出A、B点的坐标，根据菱形的面积=BC×(yA−yB)=8，得出关于k的方程，解方程取负值即可．
方法二：过点A作AE⊥BC于点E，根据面积求出BC，根据勾股定理求出BE，设出A点和B点坐标，再利用反比例函数过A点和B点求出k值即可．
本题主要考查反比例函数图象上点的坐标特征，以及菱形的性质．
16.【答案】3 52或154
【解析】解：设BM，EF交于点O，
∵将矩形纸片ABCD折叠，使点B与点M重合，折痕与AD，BC分别交于点E，F，
∴OM=OB，EF⊥BM，
∵四边形ABCD是矩形，
∴AD//BC，
∴∠M=∠OBF，∠MEO=∠BFO，
又OM=OB，
∴△OEM≌△OFB(AAS)，
∴OE=OF，
①当M点在D点的右侧时，如图所示，
∵BC=5，DM=1，
∴AM=AD+DM=BC+DM=6，
Rt△ABM中，
BM= AM2+AB2= 62+32=3 5，
∴OM=12BM=3 52，
∵tanM=EOOM=ABAM，
∴EO3 52=36，
∴EO=3 54，
∴EF=2EO=3 52；
当M点在D点的左侧时，如图所示，
∵AB=3，BC=5，DM=1，
∴BM= AM2+AB2= (5−1)2+32=5，
∴OM=12BM=52，
∵tan∠EMO=EOOM=ABAM，
∴EO52=34，
∴EO=158，
∴EF=2EO=154，
综上所述，EF的长为3 52或154．
故答案为：3 52或154．
分点M在D点右边与左边两种情况，分别画出图形，根据勾股定理，锐角三角函数即可求解．
本题考查矩形中的折叠问题，涉及勾股定理，锐角三角函数等知识，分类讨论是解题的关键．
17.【答案】解：(1)∵CD⊥AB，
∴∠CEO=∠AED=90°，
∴∠D=90°−∠A=90°−48°=42°，
∴∠AOC=2∠D=84°，
∴∠OCE=90°−84°=6°；
(2)∵CD⊥AB，
∴CE=DE=12CD=2 2，
设圆O的半径为r，则OE=r−2，OC=r，
在Rt△OCE中，(r−2)2+(2 2)2=r2，解得r=3，
即圆O的半径为3．
【解析】(1)先利用互余计算出∠D=90°−∠A=42°，再根据圆周角定理计算出∠AOC=2∠D=84°，然后利用互余计算∠OCE的度数；
(2)先利用垂径定理得到CE=DE=12CD=2 2，设圆O的半径为r，则OE=r−2，OC=r，在Rt△OCE中根据勾股定理得(r−2)2+(2 2)2=r2，然后解关于r的方程即可．
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．
18.【答案】14
【解析】解：(1)由题意得，
随机抽取一张卡片，卡片上的数字是“4”的概率是14．
故答案为：14．
(2)画树状图如下：
共有12种等可能的结果，其中两张卡片上的数字是“2”和“3”的结果有2种，
∴小明随机抽取两张卡片，两张卡片上的数字是“2”和“3”的概率为212=16．
(1)根据概率公式求解即可．
(2)画树状图，表示出所有等可能的结果数，以及两张卡片上的数字是“2”和“3”的结果数，再结合概率公式即可得出答案．
本题考查列表法与树状图法、概率公式，熟练掌握列表法与树状图法是解答本题的关键．
19.【答案】解：∵BC=12cm，O为BC的中点，
∴BO=CO=6cm．
∵AO=4cm，DO=9cm，
∴AOCO=BODO=23．
∵∠AOB=∠COD，
∴△AOB∽△COD
∴ABCD=AOCO，即5CD=23．
∴CD=5×32=7.5(cm)．
∴△CDO的周长是6+712+9=2212(cm)．
【解析】由给出的条件和图形隐藏的对顶角∠AOB=∠COD，可判断△AOB∽△COD，利用相似三角形的性质：对应边的比值相等，可求的CD值，进而求出△CDO的周长．
本题考查相似三角形的判断和性质，常见的判断方法为：SSS，SAS，AA，HL.相似三角形的性质：对应角相等，对应边的比值相等．在证明时要注意图形隐藏条件的挖掘，如本题图形中的对顶角∠AOB=∠COD．
20.【答案】解：(1)对于y=2x+4，当x=0时，y=4，
令y=2x+4=0，则x=−2，
即点A、B的坐标分别为：(−2,0)、(0,4)，
则AB2=OA2+OB2=20，
则正方形ABCD的面积=AB2=20；
(2)过点D作DH⊥x轴于点H，

∵四边形ABCD为正方形，则AB=AD，
∵∠DAH+∠BAO=90°，∠BAO+∠ABO=90°，
∴∠DAH=∠ABO，
∵∠AHD=∠BOA=90°，
∴△AHD≌△BOA(AAS)，
∴AH=BO=4，DH=OA=2，
则点D(−6,2)；
(3)同理可得，点C(−4,6)，
将点D的坐标代入反比例函数表达式得：k=−6×2=−12，
则反比例函数的表达式为：y=−12x，
当y=6时，即6=−12x，
解得：x=−2，
即点E(−2,6)，
即EF=2．
【解析】(1)求出点A、B的坐标分别为：(−2,0)、(0,4)，即可求解；
(2)证明△AHD≌△BOA(AAS)，得到AH=BO=4，DH=OA=2，即可求解；
(3)求出反比例函数的表达式为：y=−12x，当y=6时，即6=−12x，即可求解．
本题是反比例函数综合题，考查了待定系数法，一次函数的图象和性质，勾股定理，正方形的性质，全等三角形的判定和性质等，熟练掌握待定系数法求一次函数解析式的方法、勾股定理的应用、三角形全等的判定与性质等是解题关键．
21.【答案】(1)证明：如图，连接OA，
∵AE⊥CD，
∴∠DAE+∠ADE=90°．
∵DA平分∠BDE，
∴∠ADE=∠ADO，
又∵OA=OD，
∴∠OAD=∠ADO，
∴∠DAE+∠OAD=90°，
∴OA⊥AE，
∴AE是⊙O切线；
(2)解：如图，取CD中点F，连接OF，
∴OF⊥CD于点F．
∴四边形AEFO是矩形，
∵CD=6，
∴DF=FC=3．
在Rt△OFD中，OF=AE=4，
∴OD= OF2+DF2= 42+32=5，
在Rt△AED中，AE=4，ED=5−3=2，
∴AD= 42+22= 20=2 5，
∴AD的长是2 5．
【解析】(1)连接OA，根据已知条件证明OA⊥AE即可解决问题；
(2)取CD中点F，连接OF，根据垂径定理可得OF⊥CD，所以四边形AEFO是矩形，利用勾股定理即可求出结果．
本题考查了切线的判定与性质，垂径定理，勾股定理，解决本题的关键是掌握切线的判定与性质．
22.【答案】解：(1)∵一次函数y=kx+6的图象与反比例函数y=mx(m>0)的图象交于A(3,4)，B两点，
∴4=3k+6，4=m3，
∴k=−23，m=12，
∴一次函数的解析式为y=−23x+6，反比例函数的解析式为y=12x，
把y=0代入y=−23x+6得：0=−23x+6，
解得x=9，
∴点C的坐标为(9,0)；
(2)由(1)得到一次函数的解析式为y=−23x+6，反比例函数的解析式为y=12x，
y=−23x+6y=12x，解得x=3y=4或x=6y=2，
∴A(3,4)，B(6,2)，
∴不等式kx+6>mx的解集为3(3)如图，延长DA交x轴于点F，

将直线AB沿y轴向上平移3个单位长度后解析式为y=−23x+6+3=−23x+9，
由y=−23x+9y=12x，解得x=32y=8或x=12y=1，
∴D(32,8)，
设直线AD的解析式为y=ax+b，
把A、D的坐标代入得3a+b=432a+b=8，
解得a=−83b=12，
∴直线AD的解析式为y=−83x+12，
令y=0，则0=−83x+12，
解得x=92，
∴F(92,0)，
∴CF=9−92=92，
∴S△ACD=S△CDF−S△CAF=12×92×8−12×92×4=9．
【解析】(1)把点A的坐标代入y=kx+6，y=mx(m>0)求出k、m的值；把y=0代入直线AB的解析式，求出点C的坐标；
(2)分析不等式kx+6>mx的解集，图象上是一次函数y=kx+6图象在反比例函数y=mx(m>0)图象上方的部分，即在点A(3,4)，B之间的部分，求出B点横坐标，得到不等式的解集；
(3)延长DA交x轴于点F，先求出AB平移后的关系式，再求出点D的坐标，然后求出AD的解析式，得出点F的坐标，根据S△ACD=S△CDF−S△CAF求出结果．
本题考查了一次函数与反比例函数的综合应用，利用待定系数法求函数的解析式，整理掌握待定系数法以及数形结合是解答本题的关键．
23.【答案】证明：(1)连接OE．

∵在△ABC中，AB=AC，
∴∠B=∠C．
∵OB=OE，
∴∠OBE=∠OEB．
∴∠OEB=∠C，
∴OE//AC．
∴∠OEF+∠AFE=180°．
∵EF⊥AC于点F，
∴∠EFA=90°．
∴∠OEF=90°，
∴OE⊥EF．
∵OE⊥EF于点E，OE是⊙O的半径，
∴EF是⊙O的切线；
(2)如图2，连接DE，

∵四边形ABED是圆内接四边形，
∴∠EDF=∠B，且∠B=∠C，
∴∠EDF=∠C，
∴DE=EC，
∴△DEC是等腰三角形；
(3)如图3，连接AE，

∵AB是直径，
∴∠AEB=90°，且AB=AC，
∴BE=CE=3，
∵EC=DE，EF⊥AC，
∴CF=DF=12CD=1，
∵∠B=∠C，∠AEB=∠EFC=90°，
∴△ABE∽△ECF，
∴ABEC=BECF，
∴AB3=31
∴AB=9，
∴⊙O的半径OA=92．
【解析】(1)连接OE.根据等腰三角形的性质得到∠OEB=∠C，根据平行线的性质得到∠OEF+∠AFE=180°.根据切线的判定定理即可得到结论；
(2)由圆的内接四边形的性质可得∠EDF=∠B=∠C，可得DE=EC，可证△DEC是等腰三角形；
(3)通过证明△ABE∽△ECF，可得ABEC=BECF，可求AB=9，即可求解．
本题是圆的综合题，考查了圆的有关性质，等腰三角形的性质判定和性质，相似三角形的判定和性质等知识，添加恰当辅助线是本题的关键．
24.【答案】(1)证明：连接BD，
∵AB=CB，AD=CD，
∴BD⊥AC，
∴∠ADB=90°，
∴AB是⊙O的直径．
(2)证明：∵∠E=∠A，∠C=∠A，
∴∠E=∠C，
∴DC=DE．
(3)解法一：∵∠E=∠A，∠C=∠C，
∴△EDC∽△ABC，
∵BC=5，CD=4，
∴CECA=CDBC=45，CA=2CD=8，
∴CE=45×8=325，
∴BE=CE−BC=325−5=75，
∴BE长是75．
解法二：作DF⊥BC于点F，则∠CFD=90°，
∵∠BDC=90°，BC=5，CD=4，
∴BD= 52−42=3，
∵12BC⋅DF=12CD⋅BD=S△BCD，
∴DF=CD⋅BDBC=4×35=125，
∴CF= 42−(125)2=165，
∴BE=CE−BC=2×165−5=75，
∴BE长是75．
【解析】(1)连接BD，由AB=CB，AD=CD，根据等腰三角形的“三线合一”证明BD⊥AC，则∠ADB=90°，所以AB是⊙O的直径；
(2)根据圆周角定理证明∠E=∠A，根据“等边对等角”得∠C=∠A，所以∠E=∠C，则DC=DE；
(3)可由∠E=∠A，∠C=∠C，证明△EDC∽△ABC，根据相似三角形的对应边成比例求CE的长，再由BE=CE−BC求BE的长；也可以作DF⊥BC于点F，由勾股定理求得BD=3，再列面积等式12BC⋅DF=12CD⋅BD=S△BCD，则DF=CD⋅BDBC=4×35=125，所以CE=2×165=325，则BE=CE−BC=75．
此题重点考查等腰三角形的判定与性质、圆周角定理、相似三角形的判定与性质、勾股定理、根据面积等式求线段的长度等知识与方法，正确地作出所需要的辅助线是解题的关键．近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.5
0.4
0.25
0.2
0.1