吉林省松原市乾安县2023-2024学年七年级上学期数学期末试题（含解析）

这是一份吉林省松原市乾安县2023-2024学年七年级上学期数学期末试题（含解析），共19页。
考试注意事项：
1、考生须诚信考试,遵守考场规则和考试纪律，并自觉服从监考教师和其他考试工作人员
管理；
2、监考教师发卷后，在试卷指定的地方填写本人准考证号、姓名等信息；考试中途考生不准以任何理由离开考场；
3、考生答卷用笔必须使用同一规格同一颜色的笔作答(作图可使用铅笔) ，不准用规定以外的笔答卷，不准在答卷上作任何标记。考生书写在答题卡规定区域外的答案无效。
4、考试开始信号发出后,考生方可开始作答。
一、选择题（共6小题，每小题2分，共12分）.
1．下列四个算式中，其结果是负数的是（ ）
A．B．C．D．
2．下面计算正确的（ ）
A．B．C．D．
3．分别从正面、上面、左面观察下列物体，得到的平面图形完全相同的是（ ）
A．①B．②C．③D．④
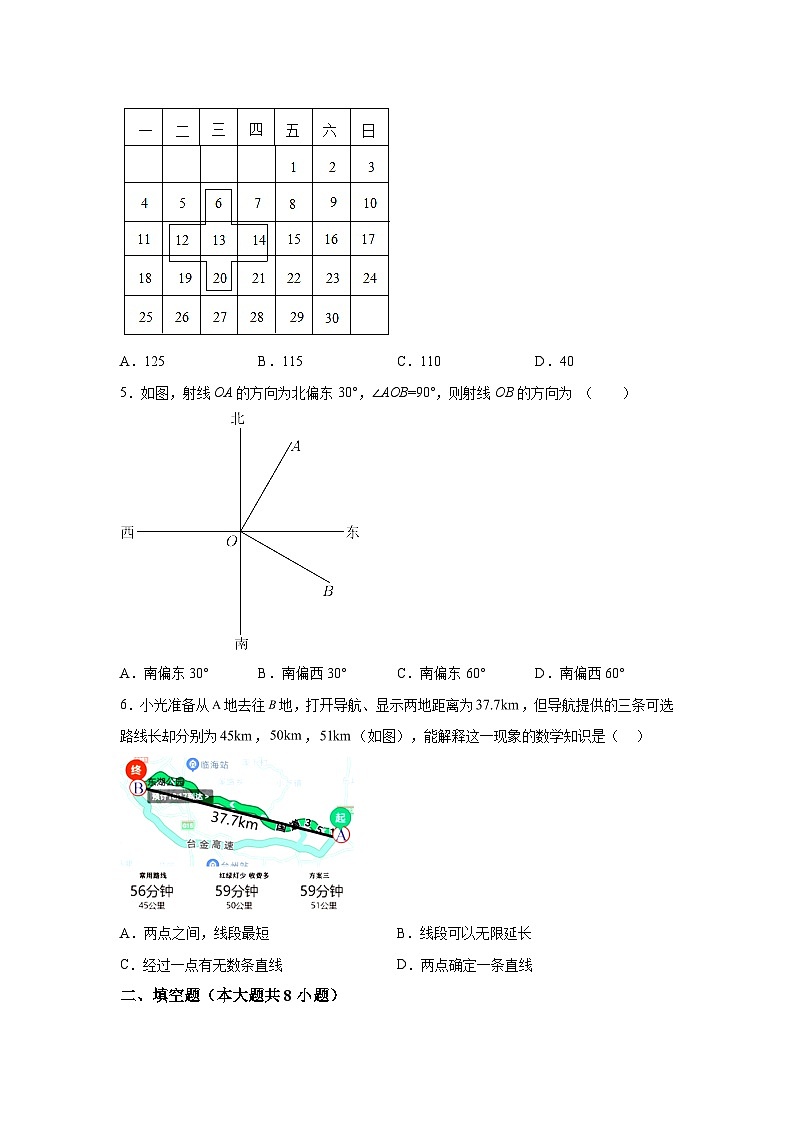
4．如图是某月的月历，用形如“十”字型框任意框出5个数．对于任何一个月的月历，这5个数的和不可能是（ ）
A．125B．115C．110D．40
5．如图，射线OA的方向为北偏东30°，∠AOB=90°，则射线OB的方向为 （ ）
A．南偏东30°B．南偏西30°C．南偏东60°D．南偏西60°
6．小光准备从地去往地，打开导航、显示两地距离为，但导航提供的三条可选路线长却分别为，，（如图），能解释这一现象的数学知识是（ ）

A．两点之间，线段最短B．线段可以无限延长
C．经过一点有无数条直线D．两点确定一条直线
二、填空题（本大题共8小题）
7．如果某天的最低气温为，中午12点的气温比最低气温高了．那么中午12点的气温为 ．
8．5G是第五代移动通信技术，5G网络下载速度可以达到每秒1300000以上，这意味着下载一部高清电影只需1秒，将1300000用科学记数法表示应为 ．
9．写出一个含字母x、y的三次单项式 提示：只要写出一个即可
10．关于x的一元一次方程2x＋m＝6的解为x＝2，则m的值为 ．
11．在日常生活和生产中有很多现象可以用数学知识进行解释．如图，要把一根挂衣帽的挂钩架水平固定在墙上，至少需要钉 个钉子．用你所学数学知识说明其中的道理 ．
12．《九章算术》是一部与现代数学的主流思想完全吻合的中国数学经典著作．其中有一道阐述“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？意思是：有若干人共同购买某种物品，如果每人出8钱，则多3钱；如果每人出7钱，则少4钱，问共有多少人？物品的价格是多少钱？用一元一次方程的知识解答上述问题设共有x人，依题意，可列方程为 ．
13．如图，延长线段AB到C，使BC＝AB，D为线段AC的中点，若DC＝3，则AB＝ ．
14．如图，用火柴棍拼成一个由三角形组成的图形，拼第一个图形共需要3根火柴棍，拼第二个图形共需要5根火柴棍；拼第三个图形共需要7根火柴棍；……照这样拼图，则第n个图形需要 根火柴棍．
三、解答题（每小题5分，共20分）
15．计算：
(1)
(2)
16．先化简，再求值：，其中．
17．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个二次三项式，形式如下：
．
(1)求所捂的二次三次式；
(2)请给x选择一个你喜欢的数代入，求所捂二次三项式的值．
18．补全解题过程．
已知：如图，平分．求的度数．
解：，
______．
平分，
（______）（填写推理依据）
______．
______．
______，
四、解答题（每小题7分，共28分）
19．如图，点A，B，C是同一平面内三个点，按要求画图，并回答问题．
（1）画直线AB；
（2）画射线AC，用圆规在线段AC的延长线上截取CD＝AC（保留作图痕迹）；
（3）连接BD，观察图形发现，AD＋BD＞AB，得出这个结论的依据是 ．
20．科技的发展给人们生活带来了巨大的变化，许多农商利用网络对产品进行销售，实现脱贫致富．小王把自家种的柚子放到网上销售，计划每天销售100千克，但实际每天的销售量与计划销售量相比有出入，下表是第一周柚子的销售情况(超过计划量记为正，不足计划量记为负．单位：千克)．
(1)第一周柚子销售量最多的一天比最少的一天多销售多少千克？
(2)小王第一周一共销售柚子多少千克？
(3)若小王按8元/千克进行包邮销售，平均运费为3元/千克，则小王第一周销售柚子一共盈利多少元？
21．如图，在一条数轴上，点为原点，点、、表示的数分别是，，．

（1）求的长（用含的代数式表示）
（2）若，求的长．
22．已知：如图，OC是∠AOB的平分线．
（1）当∠AOB = 60°时，求∠AOC的度数；
（2）在（1）的条件下，过点O作OE⊥OC，补全图形，并求∠AOE的度数；
（3）当∠AOB =时，过点O作OE⊥OC，直接写出∠AOE的度数（用含代数式表示）．
五、解答题（每小题8分，共16分）
23．解方程：
(1)5x﹣2（x﹣1）＝3；
(2)．
24．某校六年级准备观看电影《万里归途》，由各班班长负责买票，每班人数都多于40人，票价每张30元，一班班长问售票员买团体票是否可以优惠，售票员说：40人以上的团体票有两种优惠方案可选择：方案一：全体人员可打8折；方案二：若打9折，有5人可以免票．
(1)若二班有42名学生，则他该选择哪个方案？
(2)一班班长思考一会儿说，我们班无论选择哪种方案要付的钱是一样的你知道一班有多少人吗？
六、解答题（每小题10分，共20分）
25．【问题】如图①，点C是线段AB上一点，点M，N分别是线段AC，BC的中点，若线段AB=10cm，则线段MN的长为 cm．
【拓展】在【问题】中，若线段AB=a cm，其他条件不变，求线段MN的长（用含字母a的式子表示）．
【应用】（1）如图②，∠AOB=α，点C在∠AOB内部，射线OM，ON分别平分∠AOC，∠BOC，则∠MON的大小为 （用含字母α的式子表示）．
（2）如图③，在（1）中，若点C在∠AOB外部，且射线OC与射线OB在OA所在直线的同侧，其他条件不变，则（1）中的结论是否成立，若成立，请写出证明过程；若不成立，请说明理由．
26．如图，已知数轴上点A表示的数为．点B表示的数为2．动点P从点A出发，以每秒4个单位长度的速度沿数轴向右匀速运动，动点从点出发，以每秒2个单位长度的速度沿数轴向右匀速运动．同时出发，设运动时间为秒，解答下列问题：

(1)数轴上两点间的距离为______；
(2)当点表示的数和点表示的数互为相反数时，求的值；
(3)当点追上点时，求的值．
参考答案与解析
1．D
【分析】根据绝对值的性质，相反数的定义及乘方计算法则分别计算判断．
【详解】解：A、，故不符合题意；
B、，故不符合题意；
C、，故不符合题意；
D、，故符合题意；
故选：D．
【点睛】此题考查了有理数的计算，正确掌握对值的性质，相反数的定义及乘方计算法则是解题的关键．
2．D
【分析】根据整式的加减：合并同类项逐项判断即可．
【详解】A、，此项错误
B、与不是同类项，不可合并，此项错误
C、，此项错误
D、，此项正确
故选：D．
【点睛】本题考查了整式的加减：合并同类项，熟记运算法则是解题关键．
3．A
【分析】图①、图②、图③、图④可以近似的看作正方体，圆锥体，长方体、圆柱体，根据它们三视图的形状判断即可．
【详解】解：图①、图②、图③、图④可以近似的看作正方体，圆锥体，长方体、圆柱体，
正方体的三视图都是正方形的，
圆锥体的主视图、左视图是三角形的，而俯视图是圆形的，
长方体的三视图虽然都是长方形的，但它们的大小不相同，
圆柱的主视图、主视图是长方形的，但俯视图是圆形的，
因此从正面、上面、左面看所得到的平面图形完全相同的是正方体，
故选：A．
【点睛】本题考查简单组合体的三视图，掌握相关知识是解题关键．
4．A
【分析】设这5个数中间的一个为，则上面的数是，下面的数是，前面一个是，后面一个是，从而可得五个数的和为：，再列方程求解 并检验在表格中的位置，从而可得答案．
【详解】解：设这5个数中间的一个为，则上面的数是，下面的数是，前面一个是，后面一个是，
这五个数的和为：．
、如果，那么，而“十”字型框中25在第一列，不能是中间的数，即这5个数的和不可能是125，故本选项符合题意；
、如果，那么，23可以是“十”字型框中间的数，即这5个数的和可能是115，故本选项不符合题意；
、如果，那么，22可以是“十”字型框中间的数，即这5个数的和可能是110，故本选项不符合题意；
、如果，那么，8可以是“十”字型框中间的数，即这5个数的和可能是40，故本选项不符合题意；
故选：．
【点睛】本题考查的是列代数式及一元一次方程的应用，掌握利用一元一次方程解决日历问题是解题的关键．
5．C
【分析】先根据方位角求出∠3，利用余角求出∠4，利用已知得出∠1的度数，进而得出OB的方向角．
【详解】解：如图所示：
∵OA是北偏东30°方向的一条射线，
∴∠3=30°，
∵∠3+∠4=90°
∴∠4=60°，
∵∠AOB=90°，即∠1+∠4=90°
∴∠1=90°-∠4=30°，
∵∠1+∠2=90°，
∴∠2=90°-∠1=60°，
∴OB的方向角是南偏东60°．
故选：C．
【点睛】此题主要考查了方向角，正确利用角的和差得出∠1度数是解题关键．
6．A
【分析】本题主要考查了两点之间，线段最短，根据两点之间，线段最短即可得到答案．
【详解】解：由题意可知，能解释这一现象的数学知识是两点之间，线段最短，
故选：A．
7．##
【分析】本题主要考查了有理数加法的实际应用，用最低气温加上升高的温度即可得到答案．
【详解】解；，
∴中午12点的气温为，
故答案为：．
8．
【分析】科学记数法就是将一个数字表示成a×10 n的形式，其中1≤|a|＜10，n表示整数． n的值为这个数的整数位数减1，由此即可解答．
【详解】1300000=．
故答案为：．
【点睛】本题考查了科学记数法，科学记数法就是将一个数字表示成a×10 n的形式，正确确定a、n的值是解决问题的关键．
9．答案不唯一，例如，等
【详解】分析：只要根据单项式的定义写出此类单项式即可，例如y2x（答案不唯一）．
详解：只要写出的单项式只含有两个字母x、y，并且未知数的指数和为3即可．
故答案为x2y，xy2（答案不唯一）．
点睛：本题考查的是单项式的定义及单项式的次数，属开放性题目，答案不唯一．
10．2
【分析】将代入方程可得一个关于的一元一次方程，解方程即可得．
【详解】解：由题意，将代入方程得：，
解得，
故答案为：2．
【点睛】本题考查了一元一次方程的解、解一元一次方程，掌握理解方程的解的概念（使方程中等号左右两边相等的未知数的值叫做方程的解）是解题关键．
11． 2 两点确定一条直线
【分析】根据两点确定一条直线解答．
【详解】解：至少需要钉2个钉子，所学的数学知识为：两点确定一条直线，
故答案为：2，两点确定一条直线．
【点睛】此题考查了线段的性质：两点确定一条直线，熟记性质是解题的关键．
12．8x-3=7x+4
【分析】根据物品的价格相等列方程．
【详解】解：设共有x人，依题意，可列方程为8x-3=7x+4，
故答案为：8x-3=7x+4．
【点睛】此题考查了古代问题的一元一次方程，正确理解题意是解题的关键．
13．4
【分析】根据线段中点的性质，可得AC的长，再根据题目已知条件找到BC和AC之间的关系，用AC减去BC就得AB的长度
【详解】解：由D为AC的中点，得
AC=2DC
=2×3
=6
又∵BC=AB，AC=AB+BC．
∴ BC=AC
=×6
=2
由线段的和差关系，得
AB=AC-BC
=6-2
=4
故答案为：4．
【点睛】本题先根据线段中点的定义求出有关线段的长，再根据线段之间倍数关系，列出求解所求线段的式子即可．
14．2n+1
【分析】分别得到第一个、第二个、第三个图形需要的火柴棍，找到规律，再总结即可．
【详解】解：由图可知：
拼成第一个图形共需要3根火柴棍，
拼成第二个图形共需要3+2=5根火柴棍，
拼成第三个图形共需要3+2×2=7根火柴棍，
...
拼成第n个图形共需要3+2×（n-1）=2n+1根火柴棍，
故答案为：2n+1．
【点睛】此题考查图形的变化规律，找出图形之间的联系，得出运算规律解决问题．
15．(1)8
(2)
【分析】（1）本题考查有理数的加减混合运算，根据运算法则即可解题．
（2）本题考查含乘方的有理数四则混合运算，根据运算法则即可解题．
【详解】（1）解：
．
（2）解：
．
16．；
【分析】本题考查了整式的加减——化简求值，解题的关键是先去括号，再合并同类项，最后将a和b的值代入计算即可．
【详解】解：原式
，
当时，原式．
17．(1)
(2)时，
【分析】（1）利用减去即可列式，去括号、合并同类项即可求解；
（2）把代入（1）中求得的式子求解即可．
【详解】（1）设所捂的二次三项式为A，
根据题意得：；
（2）当时，原式．
【点睛】本题考查了整式的加减，即去括号合并同类项．去括号法则：当括号前是“+”号时，去掉括号和前面的“+”号，括号内各项的符号都不变号；当括号前是“-”号时，去掉括号和前面的“-”号，括号内各项的符号都要变号．根据题意列出算式是解答本题的关键．
18．110；；角平分线的定义；55；；15
【分析】本题主要考查了几何图形中角度的计算，角平分线的定义，先求出，再由角平分线的定义得到，则．
【详解】解：，
．
平分，
（角平分线的定义）（填写推理依据）
．
．
．
故答案为；110；；角平分线的定义；55；；15．
19．（1）图见解析；（2）图见解析；（3）两点之间线段最短．
【分析】（1）根据直线的画法即可得；
（2）先画射线，再以点为圆心、长为半径画弧，交线段的延长线于点即可得；
（3）先连接，根据两点之间线段最短即可得．
【详解】解：（1）如图，直线即为所求；
（2）如图，射线和线段即为所求；
（3）如图，连接，观察图形发现，，得出这个结论的依据是两点之间线段最短，
故答案为：两点之间线段最短．
【点睛】本题考查了画直线与射线、作线段、两点之间线段最短，熟练掌握尺规作图和两点之间线段最短是解题关键．
20．(1)第一周柚子销售量最多的一天比最少的一天多销售20千克
(2)小王第一周一共销售柚子718千克
(3)共盈利3590元
【分析】（1）将销售量最多的一天与销售量最少的一天相减计算即可；
（2）根据第一周实际销售柚子的数量相加计算即可；
（3）将总数量乘以单价解答即可．
【详解】（1）解：（千克）．
答：第一周柚子销售量最多的一天比最少的一天多销售20千克；
（2）解：
（千克）．
答：小王第一周一共销售柚子718千克；
（3）解：
（元）．
答：小王第一周的销售额是3590元．
【点睛】此题考查正数和负数以及有理数的混合运算，此题的关键是读懂题意，列式计算．
21．（1）的长为；（2）．
【分析】根据数轴两点之间的距离公式即可得出答案；
根据两点之间距离公式表示出，代入求出的值，用表示出，代入求值即可．
【详解】解：（1）；
（2）∵，；
∴；
∴；
∵，将代入；
得．
【点睛】本题考查了数轴上两点间距离的知识点，数形结合并熟掌握相关运算法则是解题的关键．
22．（1）30°；（2）120°或60°；（3） ；.
【分析】（1）直接由角平分线的意义得出答案即可；
（2）分两种情况：OE在OC的上面，OE在OC的下面，利用角的和与差求得答案即可；
（3）类比（2）中的答案得出结论即可．
【详解】（1）∵OC是∠AOB的平分线（，
∴∠AOC∠AOB．
∵∠AOB=60°，
∴∠AOC=30°．
（2）∵OE⊥OC，
∴∠EOC=90°，
如图1，
∠AOE=∠COE+∠COA=90°+30°=120°．
如图2，
∠AOE=∠COE﹣∠COA=90°﹣30°=60°．
（3）同（2）可得：∠AOE=90°α或∠AOE=90°α．
【点睛】本题考查了角的计算以及角平分线定义，分类考虑，类比推理是解决问题的关键．
23．(1)
(2)
【分析】（1）方程去括号，移项合并，将x系数化为1，即可求出解；
（2）方程去分母，去括号，移项合并，将x系数化为1，即可求出解．
【详解】（1）5x﹣2（x﹣1）＝3
去括号，得
移项，得
合并同类项，得．
系数化为1，得．
（2）
去分母，得
去括号，得．
移项，得．
合并同类项，得．
系数化为1，得．
【点睛】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，即可求出解．
24．(1)方案二
(2)45人
【分析】（1）分别计算出方案一和方案二的花费，然后比较大小即可解答本题；
（2）设一班有人，根据已知得出两种方案费用一样，进而列出方程求解即可．
【详解】（1）解：由题意可得，
方案一的花费为：（元），
方案二的花费为：（元），
，
若二班有42名学生，则他该选选择方案二；
（2）设一班有人，根据题意得，
，
解得．
答：一班有45人．
【点睛】本题主要考查了一元一次方程的应用，根据已知得出关于的方程是解题关键．
25．问题：5；拓展：a；应用（1）α；（2）成立，见解析
【分析】问题：根据点M，N分别是线段AC，BC的中点，可以得到M=AC，CN=BC，即可得到；
拓展：根据点M，N分别是线段AC，BC的中点，可以得到M=AC，CN=BC，即可得到；
应用：（1）根据射线OM，ON分别平分∠AOC，∠BOC，得到∠MOC=∠AOC，∠NOC=∠BOC，即可得到∠MON=∠MOC+∠NOC=（∠AOC+∠BOC）=∠AOB；
（2）根据射线OM，ON分别平分∠AOC，∠BOC，得到∠MOC=∠AOC，∠NOC=∠BOC，即可得到∠MON=∠MOC-∠NOC=（∠AOC-∠BOC）=∠AOB．
【详解】解: 【问题】∵点M，N分别是线段AC，BC的中点，
∴CM=AC，CN=BC，
∴，
故答案为：5．
【拓展】∵点M，N分别是线段AC，BC的中点，
∴CM=AC，CN=BC．
∴MN=CM+CN=AC+BC =AB=a．
【应用】（1）∵射线OM，ON分别平分∠AOC，∠BOC，
∴∠MOC=∠AOC，∠NOC=∠BOC．
∴∠MON=∠MOC+∠NOC=（∠AOC+∠BOC）=∠AOB=α．
故答案为：α；
（2）成立．
∵射线OM，ON分别平分∠AOC，∠BOC，
∴∠MOC=∠AOC，∠NOC=∠BOC．
∴∠MON=∠MOC-∠NOC=（∠AOC-∠BOC）=∠AOB=α．
【点睛】本题主要考查了线段中点有关的计算和角平分线的有关的计算，解题的关键在于能够熟练掌握相关知识进行求解.
26．(1)12
(2)
(3)
【分析】本题主要考查了数轴上两点的距离计算，一元一次方程的应用，熟知数轴上两点距离计算公式是解题的关键．
（1）根据数轴上两点距离计算公式求解即可；
（2）由题意得，点P表示的数为，点Q表示的数为，再根据相反数的定义可得方程，解方程即可得到答案；
（3）根据点追上点时，点P和点Q表示的数相同，则可建立方程，解方程即可得到答案．
【详解】（1）解：∵数轴上点A表示的数为．点B表示的数为2，
∴数轴上两点间的距离为，
故答案为：；
（2）解：由题意得，点P表示的数为，点Q表示的数为，
∵点表示的数和点表示的数互为相反数
∴．
解得．
（3）解：由题意得，，
解得，．
星期
一
二
三
四
五
六
日
与计划量的差值