吉林省四平市铁西区2023-2024学年七年级上学期期末考试数学试题（含解析）

这是一份吉林省四平市铁西区2023-2024学年七年级上学期期末考试数学试题（含解析），共16页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

一、单项选择题（每题2分，共12分）
1．如果的相反数是1，则的值为（ ）
A．1B．2C．-1D．-2
2．下列四个几何体中，从正面看和从上面看都是圆的是（ ）
A．B．C．D．
3．下列合并同类项中，正确的是（ ）
A．B．C．D．
4．下列等式变形正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
5．已知点A，B，C，D在数轴上的位置如图所示，且相邻两点之间的距离均为1个单位长度．若点A，B，C，D分别表示数，b，c，d，且满足，则b的值为（ ）
A．B．C．D．
6．如图所示，OA是北偏东30°方向的一条射线，若∠AOB＝90°，则OB的方位角是（ ）
A．北偏西30°B．北偏西60°C．北偏东30°D．北偏东60°
二、填空题（每小题3分，共24分）
7． （填“”或“”）
8． ．
9．2023年杭州举办了第19届亚运会，杭州亚运会售出约3050000张门票，3050000这个数据用科学记数法表示为 ．
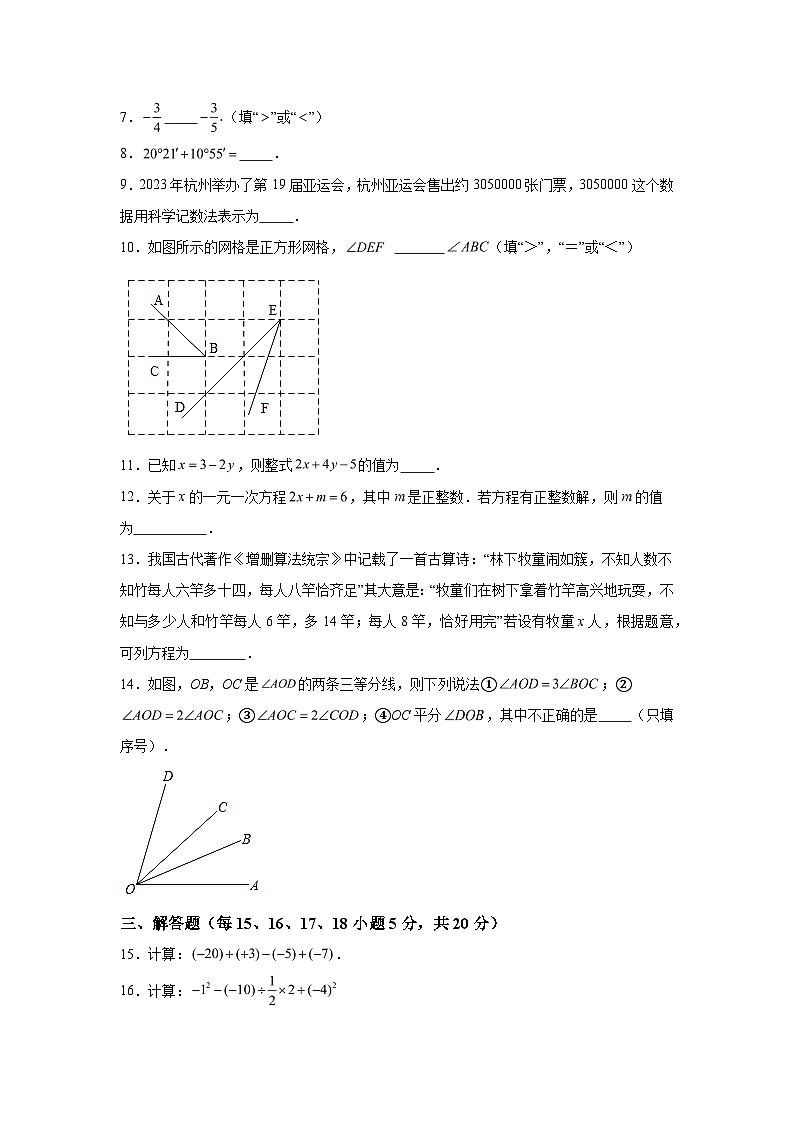
10．如图所示的网格是正方形网格， （填“＞”，“＝”或“＜”）
11．已知，则整式的值为 ．
12．关于x的一元一次方程，其中m是正整数．若方程有正整数解，则m的值为 ．
13．我国古代著作《增删算法统宗》中记载了一首古算诗：“林下牧童闹如簇，不知人数不知竹每人六竿多十四，每人八竿恰齐足”其大意是：“牧童们在树下拿着竹竿高兴地玩耍，不知与多少人和竹竿每人6竿，多14竿；每人8竿，恰好用完”若设有牧童x人，根据题意，可列方程为 ．
14．如图，OB，OC是的两条三等分线，则下列说法①；②；③；④OC平分，其中不正确的是 （只填序号）．
三、解答题（每15、16、17、18小题5分，共20分）
15．计算：．
16．计算：
17．解方程：．
18．解方程：
四、解答题（每小题7分，共28分）
19．已知一个角的余角比它的补角的还少5°，求这个角．
20．小李在解关于x的方程－1去分母时，方程右边的－1漏乘了3，因而求得方程的解为x＝－2，请你帮小李同学求出a的值，并且求出原方程的解．
21．如图，C、D在线段上，，且D为的中点，．求线段和的长．
22．柳孜隋唐大运河遗址是我市的一张文化名片，为打造古运河风光带，现有一段长为280米的河道整治任务由A、B两个工程队先后接力完成．A工程队每天整治12米，B工程队每天整治10米，两个工程队共用时25天．求A工程队整治河道多少米？
五、解答题（每小题8分，共16分）
23．如图，已知平面上四个点A，B，C，D，请按要求完成下列问题：
（1）画直线，射线，连接；
（2）在线段上求作点P，使得；（保留作图痕迹）
（3）请在直线上确定一点Q，使点Q到点P与点D的距离之和最短，并写出画图的依据．
24．如果两个方程的解相差1，则称解较大的方程为另一个方程的“后移方程”．例如：方程是方程的后移方程．
（1）判断方程是否为方程的后移方程______（填“是”或“否”）；
（2）若关于x的方程是关于x的方程的后移方程，求n的值．
（3）当时，如果方程是方程的后移方程，用等式表达a，b，c满足的数量关系____________．
六、解答题（每小题10分，共20分）
25．一副三角板、，如图1放置，三角板的一边重合．
(1)请直接写出图1中，______度；
(2)如图2，将三角板绕点逆时针旋转一定角度，
①若旋转到时，请求出的度数；
②若旋转到时，请求出的度数．
26．如图，在数轴上的点表示数，点表示数，满足．
(1)分别求出点表示的数和点表示的数；
(2)在数轴上有一动点，且点满足点到点的距离是点到点的距离的2倍，请求出所对应的有理数；
(3)若动点从点出发第一次向左运动1个单位长度，然后在新的位置第二次运动，向右运动2个单位长度，在此位置第三次运动，向左运动3个单位长度…按照如此规律不断地左右运动，直到满足第（2）的条件，请直接写出这是第几次运动．
参考答案与解析
1．A
【分析】的相反数为，则，．
【详解】解：的相反数为
故选A．
【点睛】本题考查了相反数与平方．解题的关键在于求出的值．
2．D
【分析】本题主要考查了从不同的方向看几何体，分别找到四个几何体从正面看和从上面看看到的图形是解题的关键．
【详解】解：A、圆柱从正面看看到的图形是长方形，从上面看看到的是圆，不符合题意；
B、圆台从正面看看到的图形是梯形，从上面看看到的是两个同心圆，不符合题意；
C、三棱锥从正面看看到的图形是三角形，从上面看看到的是圆，不符合题意；
D、球从正面看看到的图形是圆，从上面看看到的是圆，符合题意；
故选D．
3．C
【分析】根据合并同类项法则计算并判定即可．
【详解】解：A、，原计算错误，故此选项不符合题意；
B、，原计算错误，故此选项不符合题意；
C、，故此选项符合题意；
D、，原计算错误，故此选项不符合题意；
故选：C．
【点睛】本题考查合并同类项，熟练掌握合并同类项法则是解题的关键．
4．B
【分析】根据等式的性质逐项分析判断即可求解．
【详解】解：A. 若，则，故该选项不正确，不符合题意；
B. 若，则，故该选项正确，符合题意；
C. 若，则，故该选项不正确，不符合题意；
D. 若，则，故该选项不正确，不符合题意．
故选：B．
【点睛】本题考查了等式的性质，熟练等式的性质是解题的关键．等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等；等式的性质2：等式两边乘同一个数，或除以同一个不为的数(或式子)，结果仍相等．
5．B
【分析】由，可知a、d互为相反数，从而得到原点是AD的中点，进而得出结论．
【详解】解：∵，
∴a、d互为相反数，
∴原点是AD的中点，
∵相邻两点之间的距离均为1个单位，
∵BC =1，
∴b=，
故选：B．
【点睛】本题主要考查数轴的应用，熟练掌握互为相反数的两个点，分别位于原点的两旁，并且到原点的距离相等是解决此题的关键．
6．B
【分析】先求出∠COB＝60°，再根据具体位置确定答案．
【详解】如图，
∵∠AOB＝90°，∠AOC＝30°，
∴∠COB＝60°，
∴OB的方位角是北偏西60°，
故选：B．
．
【点睛】此题考查方位角，已知一个角求其余角，正确理解方位角的确定方法及表示方法是解题的关键．
7．
【分析】两个负数比较大小，绝对值大的反而小即可得出答案．
【详解】解：，，，
．
故答案为：．
【点睛】本题考查了有理数的比较大小，掌握两个负数比较大小，绝对值大的反而小是解题的关键．
8．
【分析】根据度、分、秒是常用的角的度量单位．度分，即，分秒，即进行计算即可．
【详解】解：原式，
故答案为：．
【点睛】本题主要考查度分秒的换算，，是解题的关键．
9．
【分析】本题考查了科学记数法的表示方法，科学记数法的表现形式为的形式，其中，为整数，确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，是非负数，当原数绝对值小于1时，是负数，表示时关键是要正确确定的值以及的值．
【详解】解：3050000这个数据用科学记数法表示为，
故答案为：．
10．＜
【分析】依据图形即可得到∠ABC＝45°，∠DEF＜45°，进而得出两个角的大小关系．
【详解】解：由图可得，∠ABC＝45°，∠DEF＜45°，
∴∠DEF＜∠ABC，
故答案为：＜．
【点睛】本题考查了角的比较，掌握比较角的大小方法是解答此题的关键．
11．1
【分析】由得；而，将代入即可得到结果．
【详解】解：
又
故答案为：．
【点睛】本题考查了代数式求值．解题的关键在于整体代入进行求解．
12．2或4##4或2
【分析】通过解一元一次方程即可解答．
【详解】解：
移项得，
化简得，
又∵m是正整数且方程也有正整数解，
∴当m=1，2，3，4，5，6时方程有解，
而当m=2，4时有正整数解．
故答案为：2或4．
【点睛】本题考查了解一元一次方程，解决本题的关键是熟练的掌握一元一次方程的解．
13．6x+14=8x
【分析】设有牧童x人，根据“每人6竿，多14竿；每人8竿，恰好用完”，竹竿的总数不变，列出方程，即可．
【详解】解：设有牧童x人，
根据题意得：6x+14=8x，
故答案是：6x+14=8x．
【点睛】本题主要考查一元一次方程的实际应用，根据等量关系，列出方程，是解题的关键．
14．②
【分析】由OB、OC是∠AOD的两条三等分线，得到∠AOB＝∠BOC＝∠COD，以此判断即可．
【详解】解：OB、OC是∠AOD的两条三等分线，
故∠AOB＝∠BOC＝∠COD
∠AOD＝∠AOB＋∠BOC＋∠COD＝3∠BOC，故①正确；
∠AOD＝3∠BOC，2∠AOC＝2（∠AOB＋∠BOC）＝4∠BOC故②不正确
，故③正确；
∠COD＝∠BOC，故④正确；
故答案为：②．
【点睛】本题考查了角的n等分线的定义，熟练掌握角等分线的定义是解决本题的关键．
15．－19
【分析】先写成省略加号和的形式，然后同号相加，再计算异号加法即可．
【详解】解：，
＝-20＋3＋5-7，
＝－27＋8，
＝－19．
【点睛】本题考查有理数的加减混合运算，掌握有理数的加法法则是解题关键．
16．55
【分析】本题主要考查了有理数的混合运算，先算乘方，再算乘除，最后算加减．
【详解】原式
.
17．
【分析】先去括号，再移项、合并同类项、系数化为1即可.
【详解】解：去括号,得：，
移项、合并同类项,得：，
系数化为1,得：.
【点睛】本题考查的是解一元一次方程，熟知去分母、去括号、移项、合并同类项、系数化为1是解一元一次方程的一般步骤是解题的关键.
18．
【分析】原式是一个含有分数的一元一次方程，对于含有分数的一元一次方程，①去分母，找出所有分母的最小公倍数，每一项都乘以最小公倍数；②去括号；③移项合并同类项；④系数化为1，按照以上四步即可解出结果.
【详解】解：
经检验：带入原方程，使得等号两边相等，所以是原方程的解.
【点睛】本题主要考查的是含分母的一元一次方程的解法，掌握这类一元一次方程解法的步骤，注意其中细节问题是解此题的关键.
19．这个角为27°．
【分析】设这个角为x，则余角为（90°﹣x），补角为（180°﹣x），根据题意可列出方程，解出即可得出答案．
【详解】解：设这个角为x，则余角为（90°﹣x），补角为（180°﹣x），
由题意得，（90°﹣x）＝（180°﹣x）﹣5°，
解得：x＝27°．
答：这个角为27°．
【点睛】本题考查了余角和补角的知识，属于基础题，注意掌握互余两角之和为90°，互补两角之和为180°．
20．a＝－2；原方程正确的解为x＝－4．
【分析】先按此方法去分母，再将x=2代入方程，求得a的值，然后把a的值代入原方程并解方程．
【详解】按小李的解法解方程2x－1＝x＋a－1，得x＝a．
又∵小李解得x＝－2，
∴a＝－2．
把a＝－2代入原方程，得
，
2x－1=x－2－3，
解得x＝－4，
即原方程正确的解为x＝－4．
【点睛】本题考查一元一次方程的解的定义，把方程的解代入原方程进行求解是解题的关键．
21．；
【分析】根据题意依次求解即可
【详解】∵D为中点，
∴，
∵，
∴，
∵，
∴，
∴．
【点睛】本题考查了线段中点的定义、线段的和差，掌握理解线段中点的定义是解题关键．
22．设A工程队整治河道180米
【分析】设A工程队整治河道x米，根据两个工程队共用时25天即可建立一元一次方程求解．
【详解】解：设A工程队整治河道x米，
根据题意得：，
．
答：设A工程队整治河道180米．
【点睛】本题考查一元一次方程与工程问题．正确理解题意是关键．
23．（1）见解析；（2）见解析；（3）画图见解析，两点之间线段最短
【分析】（1）根据题意画直线，射线，连接；
（2）在线段上截取，则点即为所求，
（3）连接交于点，根据两点之间线段最短即可求解
【详解】（1）如图，画直线，射线，连接；
（2）如图，在线段上截取，则
点即为所求，
（3）如图，连接交于点，
，根据两点之间线段最短，
三点共线时，最短
则作图的依据为：两点之间线段最短
【点睛】本题考查了画射线，直线，线段，两点之间线段最短，掌握基本作图是解题的关键．
24．（1）是；（2）-3；（3）a+b=c
【分析】（1）分别求出两个方程的解即可判断；
（2）先求出两个方程的解，然后根据后移方程的定义列式求解；
（3）先求出两个方程的解，然后根据后移方程的定义列式求解；
【详解】解：（1）∵，
∴，
∴x=，
∵，
∴，
∴x=，
∵，
∴方程是方程的后移方程，
故答案为：是；
（2）∵，
∴3x=-m-n，
∴x=，
∵，
∴x=，
∵方程是关于x的方程的后移方程，
∴，
∴，
∴-m-n+m=3
∴n=-3；
（3）∵，
∴，
∴x=，
∵，
∴，
∴x=，
∵方程是方程的后移方程，
∴，
∴，
∴-b+c=a，
∴a+b=c，
故答案为：a+b=c．
【点睛】本题考查了新定义，以及解一元一次方程，理解“后移方程”的定义是解答本题的关键．
25．(1)15
(2)①；②
【分析】本题考查了几何图中角度的计算，理解题意，找准角直角的关系是解此题的关键．
（1）算出、的度数，再由进行计算即可；
（2）①算出、的度数，再由，，进行计算即可；②由进行计算即可．
【详解】（1）解：，，
，
故答案为：15；
（2）解：①由题知，，
，
，
，
；
②由题知：，
．
26．(1)，
(2)或
(3)第8次或第23次
【分析】本题考查了绝对值的非负性以及数轴上点的移动规律，解决本题的关键是在点移动的过程中，求符合条件的点所对应的有理数时，要进行分类讨论．
（1）由非负数的性质得出，，求得的值即可；
（2）设点表示的数为，分情况讨论：当点在线段上时，当点在线段的延长线上时，当点在线段的延长线上时，分别得出一元一次方程，解方程即可得出答案；
（3）根据题意得出点每一次运动后所在的位置，然后由有理数的加法进行计算即可．
【详解】（1）解：由题得：，，
解得：，；
（2）解：设点表示的数为，
当点在线段上时，，
，
解得：，
当点在线段的延长线上时，，
，
解得：（不符合题意，舍去）；
当点在线段的延长线上时，，
，
解得：；
∴点对应的有理数为或，
（3）解：由（2）可知，当点所对应的有理数为或时，符合条件，
，
当点运动第次时，符合题意；
，
当点运动第次时，符合题意；
综上所述，当点运动第8次或第23次时，符合题意．