浙江省杭州市滨江区2023-2024学年六年级上学期数学期末模拟试卷

这是一份浙江省杭州市滨江区2023-2024学年六年级上学期数学期末模拟试卷，共16页。试卷主要包含了填空题，选择题，解答题，操作题，解决问题等内容，欢迎下载使用。
一、填空题。
1． ：40= 24（ ）=3÷8= %= （填小数）
2．在横线里填>、y>zB．y>x>zC．z>y>xD．z>x>y
14．用两张同样大小的正方形卡纸，按照下面两种不同的方式剪出甲、乙两种规格的圆片，那么甲和乙的面积比是（ ）
A．2：1B．4：1C．8：1D．16：1
15．兰兰为妈妈冲了四杯糖水，下面四杯糖水中最甜的是（ ）
A．第一杯含糖率11%B．20克糖冲成200克糖水
C．100克水中加入10克糖D．糖与水的比1：8
16．一件商品原价200元，涨价15%后再降价15%，现价（ ）原价。
A．高于B．低于C．等于D．无法比较
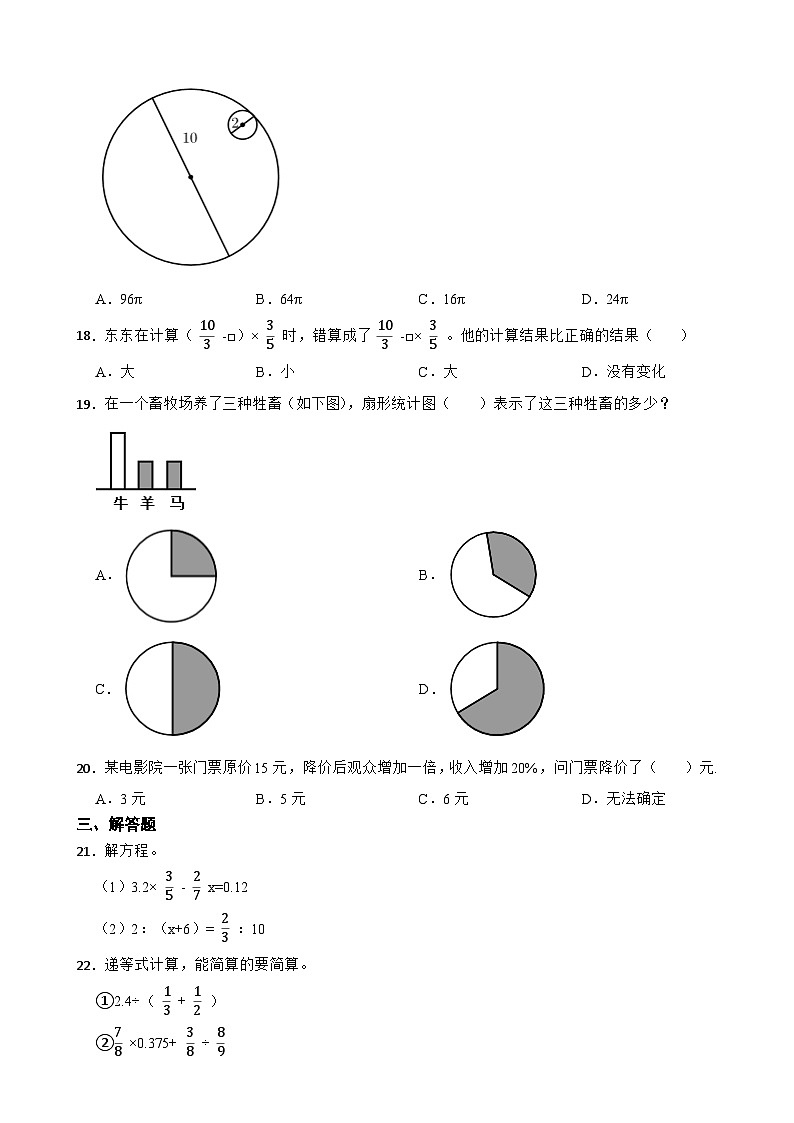
17．如图，大圆的直径为10cm，小圆的直径为2cm，让小圆紧贴着大圆内侧无滑动地滚动一周，小圆滚过的面积是（ ）cm2.
A．96πB．64πC．16πD．24π
18．东东在计算（ 103 -□）× 35 时，错算成了 103 -□× 35 。他的计算结果比正确的结果（ ）
A．大B．小C．大D．没有变化
19．在一个畜牧场养了三种牲畜（如下图），扇形统计图（ ）表示了这三种牲畜的多少？
A．B．
C．D．
20．某电影院一张门票原价15元，降价后观众增加一倍，收入增加20%，问门票降价了（ ）元.
A．3元B．5元C．6元D．无法确定
三、解答题
21．解方程。
（1）3.2× 35 - 27 x=0.12
（2）2：（x+6）= 23 ：10
22．递等式计算，能简算的要简算。
①2.4÷（ 13 + 12 ）
②78 ×0.375+ 38 ÷ 89
③（ 16 - 554 ）×54
④0.32×（95.1-82.6）
⑤（ 23 + 415 × 56 ）÷ 2021
⑥45 ÷[（ 35 + 12 ）×2]
23．图形计算（单位：厘米）
计算下图阴影部分的面积。
24．图形计算（单位：厘米）
计算下图阴影部分的面积。
四、操作题
25．操作题。
根据明明的描述，画出他从学校到家行走的路线图。（1厘米表示100米）
我从学校出发，向北偏东30°方向走200米，再向东走300长，最后向东偏南20°方向走100米就到家了。
五、解决问题
26．学校里有篮球、足球，排球共180个，已知篮球、足球、排球的个数比是5：4：3，三种球各有多少个？
27．工程队修一条隧道，第一天修了全程的25%，第二天修了全程的 13 还多10米，第三天修了60米正好修完，这条隧道一共有多少米？
28．下图是聪聪一家2019年12月的支出情况统计图。已知聪聪家购买衣物比伙食少花300元，那么文化教育的支出是多少元？
29．甲乙两城的公路长360千米，小王自己驾车从甲城去乙城，出发前他去加油站加满了一箱油，当行了240千米时，他看了一下燃油表，发现油箱里的油还剩 25 。照这样的速度，汽车到乙城途中要不要再加油？
30．书架上层书和下层书数量比是5：7，从上层拿20本书到下层后，上层是下层的 13 ，原来上下层各有多少本书，（用方程解）
31．李叔叔早上7时30分从家出发，步行去单位上班，10分钟走了全程的20%，李叔叔估计不能准时到达，于是改乘出租车前往，下图是行程与时间的变化情况，如图所示：
（1）如果李叔叔步行上班，走完全程需要 分钟。
（2）如果李叔叔全程都坐出租车， 分钟可以从家到单位。
（3）按照题中“先步行、再打车”的交通方式，李叔叔到达单位是几时几分？
答案解析部分
1．【答案】15；64；37.5；0.375
【知识点】百分数与小数的互化；百分数与分数的互化；百分数的应用--求百分率；比与分数、除法的关系
【解析】【解答】因为 3÷8=38，所以3：8=（3×5）：（8×5）=15：40，38=3×88×8=2464，38=0.375=37.5℅。
故答案为：15；64；37.5；0.375。
【分析】比的前项除以后项所得的商，叫做比值。根据分数与除法的关系，前项÷后项=前项（分子）后项（分母）。比的基本性质：比的前项和后项同时乘以或除以相同的数（0除外），比值不变。分数的性质：分数的分子和分母同时乘以或除以一个数（0除外），分数值不变。
2．【答案】=；>
【知识点】除数是分数的分数除法；商的变化规律
【解析】【解答】34÷109=34× 910=0.75×910，所以 0.75× 910= 34 ÷ 109。
因为0.97＜1，所以87÷0.97＞87； 因为 87＞1，所以 0.97÷ 87＜0.97；87＞0.97， 所以 87 ÷0.97＞ 0.97÷ 87 。
故答案为：=；＞。
【分析】除以一个不为零的数，等于乘这个数的倒数。一个不为零的数除以小于1的数，结果大于原数；一个不为零的数除以大于1的数，结果小于原数。
3．【答案】1：100；1100
【知识点】比的基本性质；比的化简与求值
【解析】【解答】0.03公顷=300平方米， 3平方米：0.03公顷 =3：300=1：100=1100。
故答案为：1：100；1100。
【分析】考查面积单位换算：1公顷=10000平方米。
4．【答案】5；5
【知识点】分数乘法与分数加减法的混合运算；百分数的应用--增加或减少百分之几
【解析】【解答】解：20×（1-34）=5米，所以比20米少34是5米；6÷（1+20%）=5千克，6千克比5千克多20%。
故答案为：5；5。
【分析】求比一个量少几分之几是多少，用这个量×（1-几分之几）；
一个量比另一个量多百分之几，那么另一个量=这个量÷（1+百分之几）。
5．【答案】20
【知识点】百分数的其他应用
【解析】【解答】14+1×100%=15×100%=20%。
故答案为：20。
【分析】药水质量 =药剂质量+水的质量，药剂质量占药水质量的百分比=药剂质量药水质量×100%。药剂和水的质量之比是1：4 ，假设药剂是1份，则药水是4份，可求出药剂质量与药水质量的比值，即可求出药剂质量占药水质量的百分比。
6．【答案】50.24
【知识点】长方形的周长；圆的周长
【解析】【解答】半径r：8÷2=4（分米）
圆面积：3.14×42
=3.14×16
=50.24（平方分米）
故答案为：50.24。
【分析】 圆沿半径剪开后拼成一个近似的长方形，长方形长为圆周长一半，长方形宽为圆半径。
圆周长=2πr，长方形周长=（长+宽）×2，圆面积=πr2。
7．【答案】90
【知识点】百分数的应用--求百分率
【解析】【解答】成活数量：40+5=45（棵）
植树总数量：45+5=50（棵）
植树活动的成活率=4550×100%=90%
故答案为：90。
【分析】 植树活动的成活率=成活树苗数量植树总数量 ×100%。
8．【答案】22.5
【知识点】组合图形面积的巧算；三角形的面积；长方形的面积
【解析】【解答】 长方形ABCD面积 =ab
三角形ABM面积=12×12a×b=14ab
三角形ADN面积=12×a×12b=14ab
三角形CMN面积=12×12a×12b=18ab
三角形甲面积=ab-14ab-14ab-18ab=38ab=38×60=22.5（平方米）
故答案为：22.5。
【分析】组合图形面积的计算：三角形甲面积= 长方形ABCD面积-三角形ABM面积-三角形ADN面积-三角形CMN面积， 假设长方形长为a米，宽为b米。点M、N分别是BC和CD边的中点，可以用a、b表示出四个三角形的面积，即可解答此题。
9．【答案】9：4
【知识点】比的应用
【解析】【解答】把重叠部分面积看作单位“1”，则大圆面积=1÷19=9，小圆面积=1÷14=4，所以大圆面积：小圆面积=9：4。
故答案为：9：4。
【分析】根据重叠部分的面积与大圆、小圆面积的分数关系解决两个圆的面积比。
10．【答案】64；36
【知识点】数形结合规律
【解析】【解答】观察图形，可得出如下规律：
第1个有：，1×1个 ■，3×3-1×1个 □ ；
第2个有：2×2个 ■， 4×4-2×2个 □ ；
第3个有：3×3个 ■ ，5×5-3×3个 □ ；
第4个有：4×4个 ■， 6×6-4×4个 □ ；
……
以此类推：
第n个有：n×n个 ■ ，（n+2）×（n+2）-n×n个 □ ;
所以第8个有：8×8=64个 ■，（8+2）×（8+2）-8×8=36个 □ 。
故答案为：64；36。
【分析】通过数形结合的规律解答此题。
11．【答案】D
【知识点】分数与小数的互化；分数与小数的大小比较；百分数与小数的互化
【解析】【解答】因为23≈0.6667， 66.7% =0.667，3047≈0.638，所以 3047＜0.6·＜23＜66.7%，四个数中3047最小。
故答案为：D。
【分析】将分数、百分数化成小数，再比较各数大小。
12．【答案】B
【知识点】百分数的其他应用
【解析】【解答】根据题目，客车速度100千米/时，高速路段的限速是120千米/时，轿车超过客车，但没有超速违章，可知：轿车的速度：100千米/时＜轿车速度＜120千米/时， 则轿车速度可能是客车的100%-120%之间。
故答案为：B。
【分析】轿车速度是客车速度的百分比=轿车速度客车速度×100%。
13．【答案】D
【知识点】分数与整数相乘；倒数的认识；除数是分数的分数除法
14．【答案】B
【知识点】圆的面积；比的应用
【解析】【解答】设正方形边长为a。甲圆半径为12a，乙圆半径为14a，甲面积=π（12a）2=14πa2，乙面积=π（14a）2=116πa2，甲面积：乙面积=14πa2：116πa2=4：1。
故答案为：B。
【分析】组合图形面积的计算，S圆=πr2。
15．【答案】D
【知识点】百分数的应用--求百分率
【解析】【解答】B：20克糖冲成200克糖水，含糖率=20200 ×100% ≈10%
C：100克水中加入10克糖，含糖率=10100+10×100%≈9.09%
D：糖与水的比1：8，含糖率=11+8×100%≈11.11% 所以含糖率大小比较为：D＞A＞B =C。
故答案为：D。
【分析】含糖率=糖的质量糖的质量+水的质量×100%。含糖率越高，糖水就越甜。
16．【答案】B
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】涨价后的价格=200×（1+15%）= 230（元），现价=230×（1-15%）=195.5（元），
195.5＜200，所以现价低于原价。
故答案为：B。
【分析】涨价后的价格=原价×（1+15%），现价=降价后的价格=涨价后的价格×（1-15%）。
17．【答案】C
【知识点】圆环的面积
【解析】【解答】解：10÷2=5cm，5-2=3cm，（52-32）×π=16π（cm2），所以小圆滚过的面积是16π（cm2）。
故答案为：C。
【分析】小圆紧贴着大圆内侧无滑动地滚动一周，那么小圆滚过的面积是圆环的面积，而圆环面积=（外圆的半径2-内圆半径2）×π，其中外圆的半径=大圆的直径÷2，内圆的半径=外圆的半径-小圆的直径，据此代入数据作答即可。
18．【答案】A
【知识点】分数乘法运算律
【解析】【解答】 （ 103 -□）× 35= 103 × 35-□× 35，比较（ 103 -□）× 35和 103 -□× 35 的这两个算式结果的大小，即是比较 103 × 35和103的大小。一个不为零的数乘以小于1的分数，结果小于原数。所以 103 × 35＜103。所以他的计算结果比正确的结果偏大。
故答案选：A。
【分析】运用乘法的分配律可解此题。
19．【答案】C
【知识点】从单式条形统计图获取信息；从扇形统计图获取信息
【解析】【解答】观察条形统计图可以得出：牛的数量是羊的2倍，羊的数量和马的数量一样。可得出牛：羊：马=2：1：1，用扇形统计图表示如C图所示。
故答案为：C。
【分析】根据条形统计图找出数量间的关系可解此题。
20．【答案】C
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：假设购买门票的有1人，1×15=15元，15×（1+20%）÷（1+1）=18÷2=9元，15-9=6元，所以门票降价了6元。
故答案为：C。
【分析】本题可以假设购买门票的有1人，降价前的收入=降价前一张门票的价钱×人数，那么降价后的门票价钱=降价前的收入×（1+收入增加百分之几）÷（人数+人数），所以门票降价的钱数=降价前的收入-降价后的门票价钱。
21．【答案】（1） 3.2× 35 - 27 x=0.12
解：3.2× 35 - 27 x+27 x=0.12+ 27 x
27 x=3.2× 35 -0.12
27 x=1.92-0.12
27 x=1.8
x=1.8 × 72
x=6.3
（2） 2：（x+6）= 23 ：10
解：（x+6） × 23=2×10
（x+6） × 23=20
x+6=20÷ 23
x+6=30
x=24
【知识点】比例的基本性质
【解析】【分析】（1）根据等式的基本性质：等式的两边同时加或减去相同的数（或式子），等式仍成立。等式的两边同时乘以（或除以）一个不为零的数（或式子），等式仍成立。
（2）根据比例的基本性质：在比例里，两个外项积等于两个内项积。
22．【答案】①2.4÷（ 13 + 12 ）
=2.4÷（ 26 + 36 ）
=2.4÷ 56
=2.4× 65
=2.88
②78 ×0.375+ 38 ÷ 89
= 78 × 38 + 38 × 98
=（ 78 + 98 ）× 38
=2× 38
= 34
③（ 16 - 554 ）×54
= 16 ×54- 554 ×54
=9-5
=4
④0.32×（95.1-82.6）
=0.32×12.5
=4
⑤（ 23 + 415 × 56 ）÷ 2021
=（ 23 + 29 ）× 2120
= 23 × 2120 + 29 × 2120
= 710 + 730
= 1415
⑥45 ÷[（ 35 + 12 ）×2]
= 45 ÷[（ 610 + 510 ）×2]
= 45 ÷（ 1110 ×2）
= 45 ÷ 115
= 45 × 511
= 411
【知识点】分数四则混合运算及应用；分数乘法运算律
【解析】【分析】①在四则混合运算中，有小括号的要先算小括号。计算分数加法时，先通分，再进行计算。除以一个不为零的数，等于乘这个数的倒数。
②利用乘法的分配律逆运算来进行计算：两个数的和与一个数相乘所得的积，等于这两个分别与这个数相乘所得的积的和，（a+b）c=ac+bc。
③利用乘法的分配律：两个数的差与一个数相乘所得的积，等于这两个数分别与这个数相乘所得的积的差，（a-b）c=ac-bc。
④在四则混合运算中，有小括号的要先算小括号。计算小数乘小数时，先按照整数乘法进行计算，看因数一共有几位小数，再从积的右边起数出几位小数，点上小数点，当位数不够时，要添“0”补足。
⑤在四则混合运算中，有小括号的要先算小括号。括号内混合运算，先算乘除法，再算加减法。除以一个不为零的数，等于乘这个数的倒数。
⑥有中括号、小括号的，要先算小括号，再算中括号。
23．【答案】解：（4+9）×4÷2
=13×4÷2
=26（平方厘米）
14 ×3.14×4×4
=14 ×4×4×3.14
=4×3.14
=12.56（平方厘米）
26-12.56=13.44（平方厘米）
故阴影部分的面积等于13.44平方厘米。
【知识点】梯形的面积；扇形的面积
【解析】【分析】 阴影部分的面积=梯形的面积- 14 圆的面积 。梯形上底等于圆形半径，圆面积=πr2， 梯形的面积 = （上底+下底）×高。阴影部分的面积=（上底+下底）×高-14πr2，代入公式即可解答此题。
24．【答案】解：如图所示，
①与②的面积相等，
则①的面积为：
6×6-3.14×62× 14
=36-28.26
=7.74（平方厘米）
所以阴影部分的面积为：
6×6-7.74×2
=36-15.48
=20.52（平方厘米）
【知识点】扇形的面积
【解析】【分析】 ①与②的面积相等，则①的面积=正方形面积-扇形面积=正方形面积- 14πr2，阴影部分的面积 =正方形面积-①的面积×2。将已知条件代入公式即可解答此题。
25．【答案】解：
【知识点】根据方向和距离画路线图
【解析】【分析】在图上画出1cm线段代表100米的比例尺。从学校出发， 向北偏东30°方向走200米，以学校为中心，上北下南，左西右东，标出四个方位。画出北偏东30°方向的角，并在北偏东30°的射线上截取2cm长度的线段，以2cm线段的端点为中心，向东截取3cm长度的线段，再以3cm线段的端点为中心，作出东偏南20°方向的角，在射线上截取1cm长度的线段，线段的终点就是明明的家。
26．【答案】解： 180÷（5+4+3）=15（个）
15×5=75（个）
15×4=60（个）
15×3=45（个）
答： 篮球的个数是75个，足球的个数是60个，排球的个数是45个。
【知识点】比的应用
【解析】【分析】 已知篮球、足球、排球的个数比是5：4：3，篮球、足球，排球共180个 。可以看成把180个篮球、足球、排球平均分成了5+4+3=12份，可求出每份的数量。每份的个数=总数量÷份数，篮球占5份，足球占4份，排球占3份，即可求出三种球各有多少。
27．【答案】解：工程队修一条隧道，我们可以设隧道全长为x米，
第一天修了全长的25%，也就是全长的 14 ，是 14 x米，
第二天修了全长的 13 ，还多10米，也就是（ 13 x+10）米，第三天修了60米正好修完，
所以 14 x+ 13 x+10+60=x，
512 x=70
x=70× 125
x=168
答：这条隧道一共有168米。
【知识点】列方程解关于百分数问题
【解析】【分析】根据题意，可得到等量关系式如下：第一天修隧道长度+第二天修隧道长度+第三天修隧道长度=隧道全长，列出方程式可解答此题。
28．【答案】解：设总收入是x；
x×35%-x×20%=300
x×15%=300
x=300÷15%
x=2000
文化教育所占的比例是：25%，所以文化教育的支出是：2000×25%=500（元）。
【知识点】百分数的其他应用
【解析】【分析】由等量关系可得：伙食支出-购买衣物支出=300 可列出方程式，解答求出12月总支出后，即可求出文化教育支出费用。
29．【答案】解：240÷（1- 25 ）
=240÷ 35
=240× 53
=400（米）
400米>360米
答：汽车到乙城不要再加油。
【知识点】分数除法与分数加减法的混合运算
【解析】【分析】根据题意，可以把一满箱油看作单位“1”， 行了240千米时用去油箱的1-25=35，可以求出一箱油能行驶的路程，再和甲乙两城的路程作比较即可解答此题。
30．【答案】解：设原来上层有5x本，下层有7x本。
（5x-20）÷（7x+20）=13
5x-20=（7x+20）×13
3×（5x-20）=7x+20
15x-60=7x+20
8x=80
x=10
5x=5×10=50（本）
7x=7×10=70（本）
答：原来上层有50本书，下层有70本书。
【知识点】应用比例解决实际问题
【解析】【分析】本题可以设原来上层有5x本，下层有7x本，题中存在的等量关系是：现在上层的本数÷现在下层的本数=现在上层是下层的几分之几，据此代入数据和字母作答即可。
31．【答案】（1）50
（2）15
（3）解；1-20%=80%
15×80%=12（分钟）
10+12=22（分钟）
7时30分+22分=7时52分。
答：李叔叔到达的时间为7时52分。
【知识点】分数四则混合运算及应用
【解析】【解答】（1）10÷20%=10÷15=50（分钟）
答：如果李叔叔步行上班，走完全程需要50分钟。
（2）1-20%=80%
12÷80% =15（分钟）
答：如果李叔叔全程都坐出租车，15分钟可以从家到单位。
【分析】（1）把全程看作单位“1”，10分钟走了全程的20%（15），利用分数除法可求出走完全程所需时间。
（2）由图可知，可得出乘坐出租车所用时间12（分钟），乘出租车所行驶的路程为1-20%=45，利用分数除法可求出全程乘出租所需时间。
（3）李叔叔早上7时30分从家出发，李叔叔到单位所用时间=步行时间+乘出租时间，起始时间加上到单位所用时间即可求出李叔叔到单位的时间点。