广东省中山市2023-2024学年八年级（上）期末数学试题（含解析）

这是一份广东省中山市2023-2024学年八年级（上）期末数学试题（含解析），共19页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
一、单项选择题(共10个小题， 每小题3 分， 满分 30分)
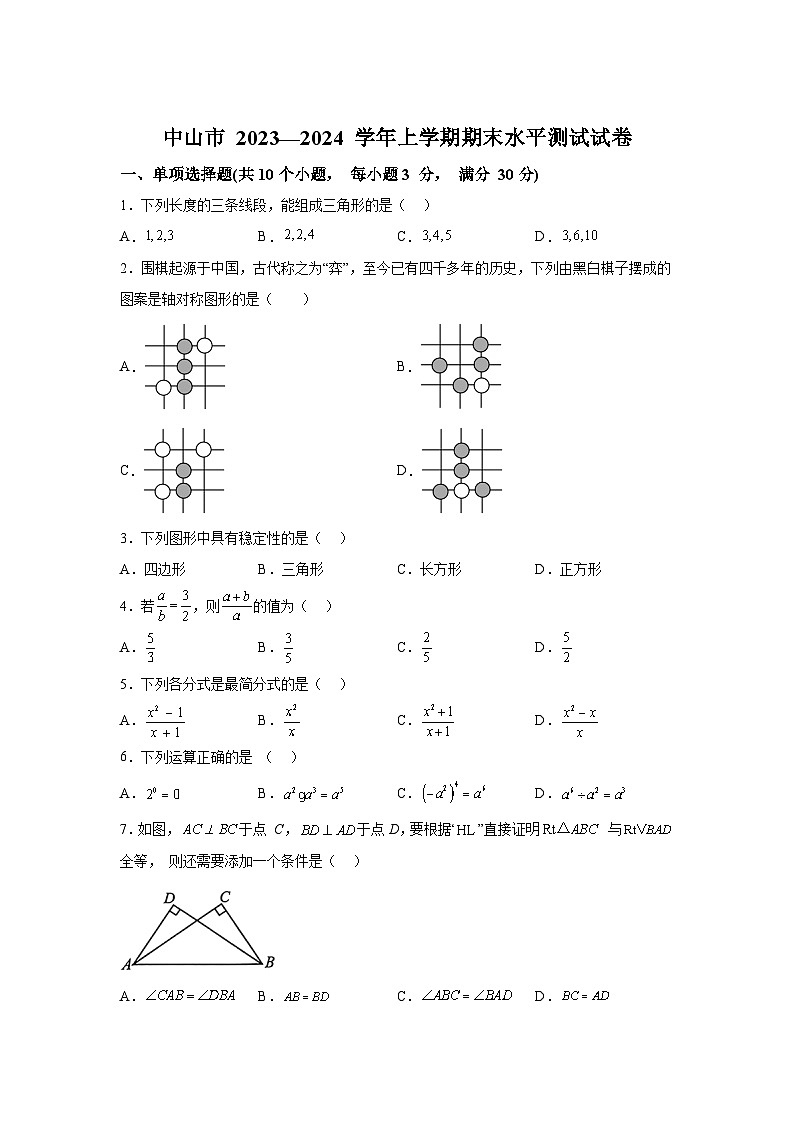
1．下列长度的三条线段，能组成三角形的是（ ）
A．B．C．D．
2．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史，下列由黑白棋子摆成的图案是轴对称图形的是（ ）
A．B．
C．D．
3．下列图形中具有稳定性的是（ ）
A．四边形B．三角形C．长方形D．正方形
4．若，则的值为（ ）
A．B．C．D．
5．下列各分式是最简分式的是（ ）
A．B．C．D．
6．下列运算正确的是 （ ）
A．B．C．D．
7．如图，于点 C，于点D，要根据“”直接证明 与全等， 则还需要添加一个条件是（ ）
A．B．C．D．
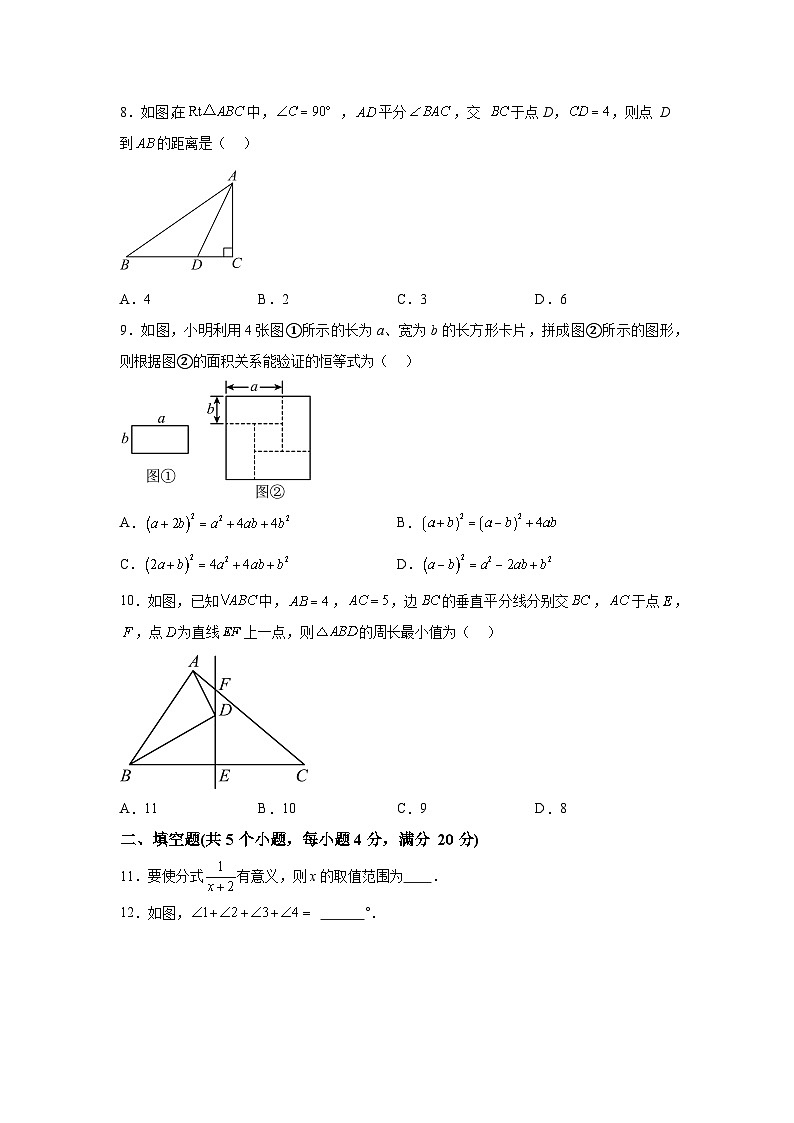
8．如图， 在中， ，平分，交 于点D，，则点 D到的距离是（ ）

A．4B．2C．3D．6
9．如图，小明利用4张图①所示的长为a、宽为b的长方形卡片，拼成图②所示的图形，则根据图②的面积关系能验证的恒等式为（ ）
A．B．
C．D．
10．如图，已知中，，，边的垂直平分线分别交，于点，，点为直线上一点，则的周长最小值为（ ）
A．11B．10C．9D．8
二、填空题(共5个小题，每小题4分，满分 20分)
11．要使分式有意义，则x的取值范围为 ．
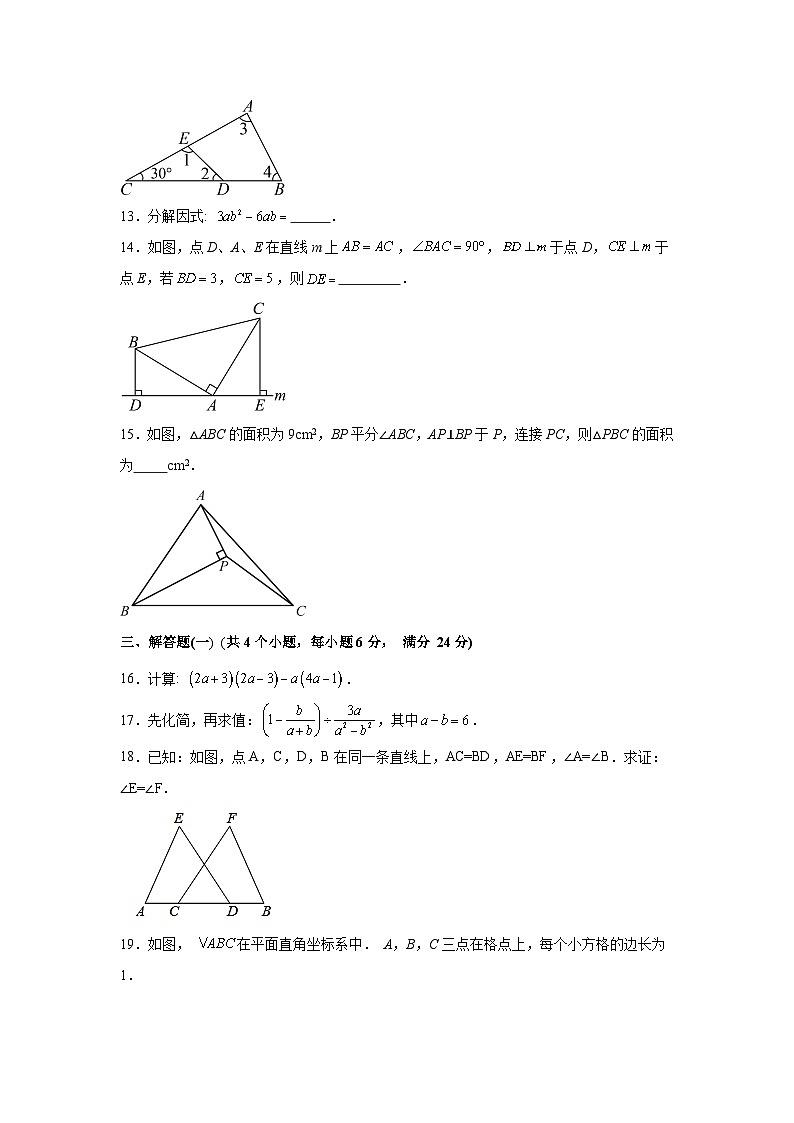
12．如图， °．

13．分解因式: ．
14．如图，点D、A、E在直线m上，，于点D，于点E，若，，则 ．
15．如图，△ABC的面积为9cm2，BP平分∠ABC，AP⊥BP于P，连接PC，则△PBC的面积为 cm2．
三、解答题(一) (共4个小题，每小题6分， 满分 24分)
16．计算: ．
17．先化简，再求值：，其中．
18．已知：如图，点A，C，D，B在同一条直线上，AC=BD，AE=BF，∠A=∠B．求证：∠E=∠F．
19．如图， 在平面直角坐标系中． A，B，C三点在格点上，每个小方格的边长为1．
(1)画出关于y轴对称的;
(2)直接写出关于x轴对称的的各顶点坐标．
四、解答题(二) (共3个小题，每小题8 分， 满分 24分)
20．已知△ABC中，∠A＝90°，∠B＝30°．
（1）作图：作△ABC的高AD交BC于点D（用尺规作图，保留作图痕迹，不写作法）；
（2）求证：BD＝3CD．
21．某校积极开展科技创新活动，在一次用电脑编程控制小型赛车进行比赛的活动中， “梦想号”和“创新号”两辆车从起点同时出发， “梦想号”到达终点时， “创新号”离终点还差．已知“梦想号”的平均速度比“创新号”的平均速度快 ．求“梦想号”和“创新号”的平均速度．
22．阅读材料：要将多项式分解因式，可以先把它的前两项分成一组，再把它的后两项分成一组， 从而得到，这时中又有公因式，于是可以提出，即， 我们称这种方法为分组法． 请你利用分组法解答下列问题：
(1)解决问题：分解因式 ．
(2)拓展运用: 已知a，b，c是的三边，且满足 ，请判断的形状并说明理由．
五、解答题(三)(共2个小题， 第 23 题10分， 第 24 题 12 分， 满分 22分)
23．如图，中， ， ， 点P从点B出发沿线段移动到点A停止，同时点Q从点C出发沿的延长线移动，并与点 P同时停止． 已知点 P，Q移动的速度相同，连接与线段 相交于点D(不考虑点 P与点A，B重合时的情况)．
(1)求证: ；
(2)求证: ；
(3)如图，过点P作于点E，在点P，Q移动的过程中，线段的长度是否变化?如果不变，请求出这个长度；如果变化，请说明理由．
24．定义: 如图1， 若 P 是内部一点， 且， 则称点P为的勃罗卡点， 同时称为的勃罗卡角．
(1)如图2， P为等边内部一点． 其中，， 请判断点P是不是等边的勃罗卡点，并说明理由；
(2)如图3，P为等边的勃罗卡点，求等边的勃罗卡角的度数；
(3)如图4，在（2）的条件下，作点 P 关于 的对称点 ，连接与 相交于点 O，连接，，记的勃罗卡点为 M，的勃罗卡点为N， 求证: 为等边三角形．
答案与解析
1．C
【分析】根据三角形的三边满足两边之和大于第三边来进行判断．
【详解】解：A、，不能构成三角形，故A错误；
B、，不能构成三角形，故B错误；
C、，能构成三角形，故C正确；
D、，不能构成三角形，故D错误．
故选：C．
2．D
【分析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，据此判断即可，解题的关键是正确理解轴对称图形的意义．
【详解】解：A，B，C选项中的图案都不能找到这样的一条直线，直线两旁的部分能够互相重合；
D选项中的图案能找到这样的一条直线，使图形沿一条直线折叠，所以是轴对称图形；
故选：D．
3．B
【分析】此题考查的是对三角形稳定性，三角形不容易产生变形，因此三角形是最稳定的；四边形没有稳定性．
【详解】解：根据三角形具有稳定性，四边形没有稳定性．
故选：B．
4．A
【分析】本题主要考查了分式的求值，先根据已知条件得到，再把代入所求式子中进行约分即可得到答案．
【详解】解：∵，
∴，
∴，
故选A．
5．C
【分析】分子与分母没有公因式的分式，叫最简分式，据此逐一进行判断即可．
【详解】解：A、，本选项不符合题意；
B、，本选项不符合题意；
C、是最简分式，本选项符合题意；
D、，本选项不符合题意；
故选：B．
【点睛】本题主要考查最简分式，掌握最简分式的概念是解题的关键．
6．B
【分析】本题主要考查0次幂的意义、整式幂的运算．根据0次幂的意义，同底数幂的乘法法则，积的乘方法则，同底数幂的除法法则逐一判断各选项即可．
【详解】解：A中，故选项运算错误，不符合题意；
B中，故选项运算正确，符合题意；
C中，故选项运算错误，不符合题意；
D中，故选项运算错误，不符合题意；
故选B．
7．D
【分析】本题主要考查了添加一个条件使得三角形全等，根据HL定理的条件进行判断即可；
【详解】解：∵，，
∴当时，．
当时，．
故选D．
8．A
【分析】本题考查了角平分线性质定理，过点D作于点E，则即为所求，根据角平分线性质得出，即可求出最后结果．
【详解】解：如图，过点D作于点E，则即为所求，
，平分，交 于点D，
,
故选：A．

9．B
【分析】此题考查对完全平方公式几何意义的理解，关键是能从整体和部分两方面来理解完全平方公式的几何意义，图②的面积可以整体表示为，也可将各部分求和表示为由此可得此题结果．
【详解】解：用整体和各部分求和两种方法表示出图②的面积各为：和，
可得，
故选：B．
10．C
【分析】本题主要考查了线段垂直平分线的性质，如图所示，连接，根据线段垂直平分线的性质得到，由三角形周长公式得到的周长，故当A、D、C三点共线时，最小，即此时的周长最小，此时点D与点F重合，最小值即为的长，据此可得答案．
【详解】解：如图所示，连接，
∵边的垂直平分线分别交，于点，，
∴，
∴的周长，
∴当A、D、C三点共线时，最小，即此时的周长最小，此时点D与点F重合，最小值即为的长，
∴的周长的最小值为，
故选C．
11．x≠﹣2
【分析】根据分式有意义的条件可得x+2≠0，解这个不等式即可求出答案．
【详解】解：由题意可知：x+2≠0，
∴x≠﹣2，
故答案为x≠﹣2．
【点睛】本题考查分式有意义的条件，解题的关键是正确理解分式有意义的条件：分母不为0．
12．
【分析】根据三角形内角和为求解即可．
【详解】解：在中有，
在中有，
将上面两式相加得：，则．
故答案为：．
【点睛】本题主要考查三角形内角和为，解题的关键是将等式相加．
13．
【分析】此题主要考查了提取公因式法分解因式，直接提公因式即可．
【详解】解：；
故答案为：．
14．8
【分析】根据垂直得到直角三角形，利用等角的余角相等证得，再利用判定证明，即可得到答案．
【详解】解：∵，，
∴，
∵，
∴，
在与中，
∵，
∴，
∴，，
∴，
故答案为：8．
【点睛】此题考查了全等三角形的判定与性质，根据判定证明是解题的关键．
15．4.5
【分析】根据已知条件证得△ABP≌△EBP，根据全等三角形的性质得到AP=PE，得出S△ABP=S△EBP，S△ACP=S△ECP，推出，代入求出即可．
【详解】
解：延长AP交BC于E，
∵BP平分∠ABC，
∴∠ABP=∠EBP，
∵AP⊥BP，
∴∠APB=∠EPB=90°，
在△ABP和△EBP中， ，
∴△ABP≌△EBP（ASA），
∴AP=PE，
∴
∴ cm2，
故答案为4.5．
【点睛】本题考查了全等三角形的性质和判定，三角形的面积的应用，注意：等底等高的三角形的面积相等．
16．
【分析】本题考查的是单项式乘以多项式，平方差公式的应用，先按照平方差公式，单项式乘以多项式进行整式的乘法运算，再合并即可，掌握“利用平方差公式进行简便运算”是解本题的关键．
【详解】解：
．
17．，2
【分析】本题主要考查了分式的化简求值．先计算括号内的，再计算除法，然后把代入化简后的结果，即可．
【详解】解：
，
当时，原式．
18．证明见解析．
【分析】求出AD=BC，然后利用“边角边”证明△ADE和△BCF全等，根据全等三角形对应角相等证明即可．
【详解】解：∵AC=BD，
∴AC+CD=BD+CD，
即AD=BC，
在△ADE和△BCF中
∴△ADE≌△BCF（SAS），
∴∠E=∠F．
【点睛】本题考查全等三角形的判定与性质．
19．(1)见解析
(2)，，
【分析】本题考查了作图一轴对称变换，记住关于x轴和y轴对称的对应点的坐标特征是解决问题的关键．
（1）利用关于y轴对称的点的坐标特征得到点、、的坐标，然后描点即可；
（2）利用关于x轴对称的点的坐标特征得到点、、的坐标．
【详解】（1）解：如图，即为所求，
（2）由图可知，，，
则关于x轴对称的的各顶点坐标，，．
20．（1）见解析；（2）证明见解析
【分析】（1）利用尺规作图的方法及相关性质作△ABC的高AD交BC于点D即可；
（2）根据30度角所对直角边等于斜边一半即可证明BD＝3CD．
【详解】（1）如图所示，AD即为所求；
（2）证明：
∵△ABC中，∠BAC＝90°，∠B＝30°，
∴BC＝2AC，∠C＝60°，
∵AD⊥BC，
∴∠CAD＝30°，
∴AC＝2CD，
∴BC＝4CD，
∴BD＝3CD．
【点睛】本题主要考查了尺规作图及含30度角的直角三角形的性质，熟练掌握相关方法及性质是解题关键．
21．“创新号”赛车的平均速度为，“梦想号”赛车的平均速度为
【分析】本题考查分式方程的应用，解题的关键是正确寻找等量关系，构建分式方程解决问题，注意解分式方程必须检验，设“创新号”赛车的平均速度为，根据时间关系列出分式方程即可解决问题．
【详解】解：设“创新号”赛车的平均速度为，则“梦想号”赛车的平均速度为，
根据题意列方程得：，
解得：，
经检验是原分式方程的解，且符合题意，
则“梦想号”赛车的平均速度为：，
答：“创新号”赛车的平均速度为，“梦想号”赛车的平均速度为．
22．(1)
(2)是等腰三角形，理由见解析
【分析】本题主要考查了因式分解及其应用，等腰三角形的定义，三角形的三边关系，解题关键是熟练掌握分解因式的几种方法．
（1）把多项式的前两项分成一组，后两项分成一组，利用提公因式法和公式法分解因式；
（2）把所给等式分组为，利用公式法分解因式，再根据三角形的三边关系，求出，即可得到答案．
【详解】（1）解：
（2）是等腰三角形，理由如下：
，
，
，
即，
为等腰三角形．
23．(1)见解析
(2)见解析
(3)为定值5，理由见解析
【分析】本题考查了全等三角形的判定与性质，等腰三角形的判定与性质，平行线的性质，线段的和差，准确作出辅助线找出全等三角形是解题关键．
（1）利用、的移动速度相同，得到，利用线段间的关系即可推出；
（2）过点P作，交于点F，利用等边对等角结合已知可证，即可得出结论；
（3）过点P作，交于点F，由（2）得，可知为等腰三角形，结合，可得出即可得出为定值．
【详解】（1）证明：、的移动速度相同，
，
，
；
（2）如图，过点P作，交于点F，
，
，
，
，
，
，
由（1）得，
，
在与中，
，
，
；
（3）解：为定值5，理由如下：
如图，过点P作，交于点F，
由（2）得：，
为等腰三角形，
，
，
由（2）得，
，
，
为定值5．
24．(1)点P不是等边的勃罗卡点，理由见解析
(2)等边的勃罗卡角的度数为
(3)见解析
【分析】（1）利用等边对等角得出，再利用等边三角形性质，中垂线的性质得出即可得出结论点P不是等边的勃罗卡点；
（2）利用点P为等边的勃罗卡点，求出，证明，即可求出等边的勃罗卡角的度数；
（3）先证明为等腰三角形，再证出， 为等边三角形，在内部作交于点N，连接，可证得点N为的勃罗卡点，且，同理可证点M为的勃罗卡点，且，进而得出最后结论．
【详解】（1）解：点P不是等边的勃罗卡点，理由如下：
，
，
，
为等边三角形，
，，
，
是的中垂线，
平分，
，
，
点P不是等边的勃罗卡点；
（2）点P为等边的勃罗卡点，
，
，
即，
，
同理可得，
在与中，
，
，
，
，
，
，
等边的勃罗卡角的度数为；
（3）证明：点P，关于对称，
为的中垂线，
，
为等腰三角形，
，
由（2）可知，
，
，
为等边三角形，同理可得为等边三角形，
如图，在内部作交于点N，连接，
为的中垂线，
，
，
，
，
，
点N为的勃罗卡点，且，
在内部作交于点M，
同理可证点M为的勃罗卡点，且，
，
，
为等边三角形．
【点睛】本题考查了等边三角形的判定与性质，等腰三角形的判定与性质，全等三角形的判定与性质，中垂线的判定与性质，对于题目中给出的勃罗卡点定义的理解与运用是解答本题的关键．