
所属成套资源:2023-2024学年七年级上学期数学期末考试(华东师大版)基础卷
2023-2024学年华东师大版数学七年级期末考试试题及解析提升卷3
展开
这是一份2023-2024学年华东师大版数学七年级期末考试试题及解析提升卷3,共16页。
1.(本题3分)已知,则的值是( )
A.4B.5C.6D.
2.(本题3分)单项式与是同类项,则的值为( )
A.B.9C.D.
3.(本题3分)某公司去年前三个月平均每月盈利万元,4、5、6月平均每月盈利2万元,7-10月平均每月盈利1.2万元,最后两个月平均每月盈利万元,则这个公司去年总盈利是( )
A.万元B.万元C.万元D.万元
4.(本题3分)下列两数比较大小,正确的是( )
A.B.C.D.
5.(本题3分)某商品打八折后的售价为160元,则该商品的原价为( )
A.200元B.240元C.220元D.260元
6.(本题3分)如图,,相交于点,,射线平分,下列结论中错误的是( )
A.与互为补角B.与互为余角
C.与互为补角D.与为对顶角
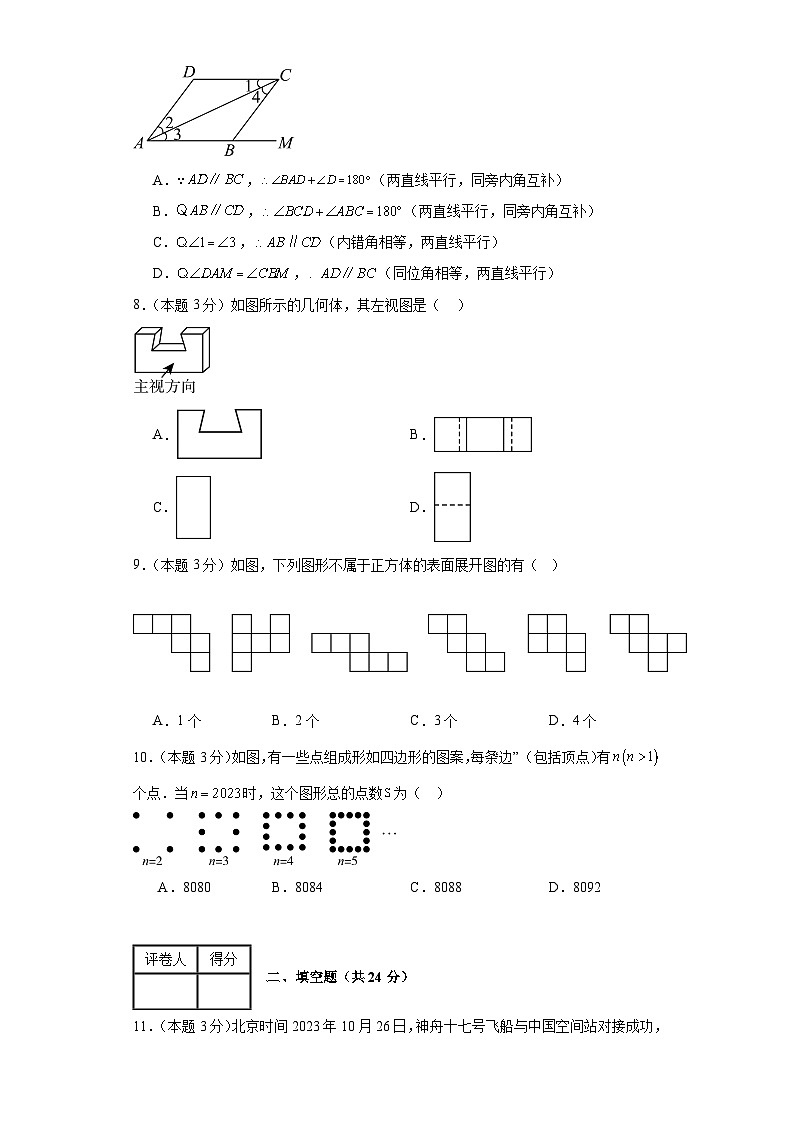
7.(本题3分)如图,下列推理及括号中所注明的推理依据错误的是( )
A.∵,(两直线平行,同旁内角互补)
B.,(两直线平行,同旁内角互补)
C.,(内错角相等,两直线平行)
D.,(同位角相等,两直线平行)
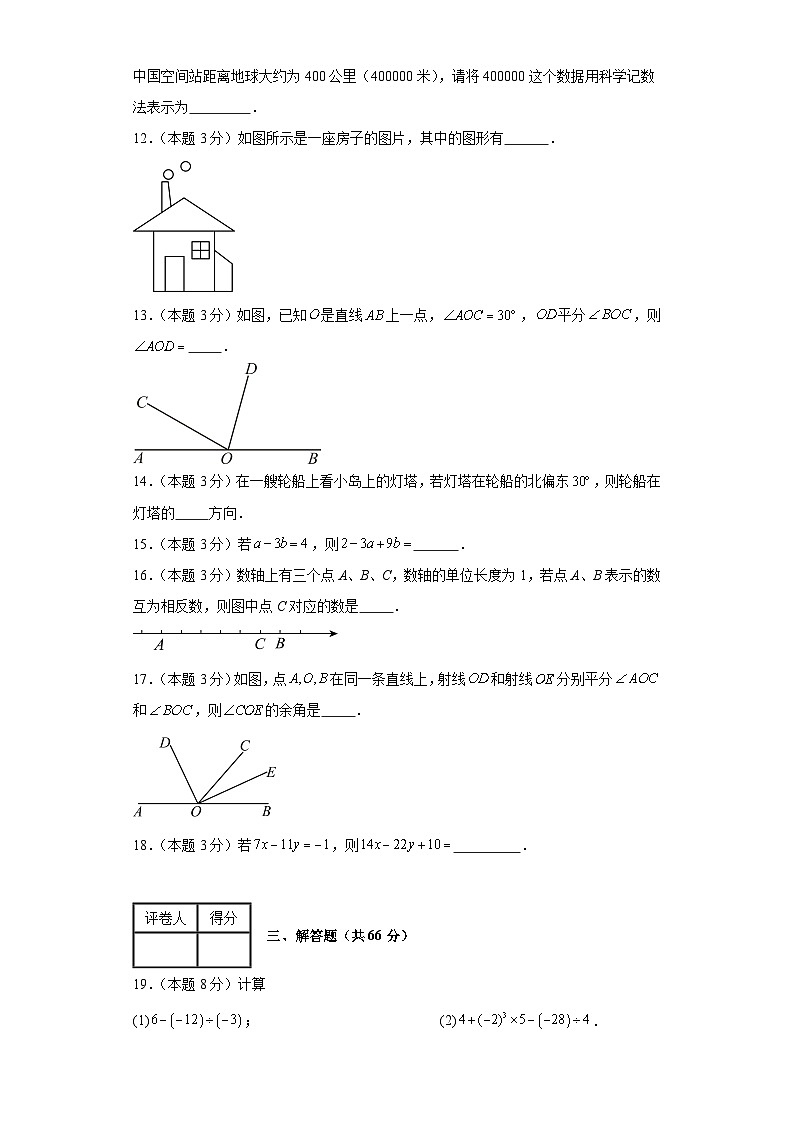
8.(本题3分)如图所示的几何体,其左视图是( )
A.B.
C.D.
9.(本题3分)如图,下列图形不属于正方体的表面展开图的有( )
A.1个B.2个C.3个D.4个
10.(本题3分)如图,有一些点组成形如四边形的图案,每条“边”(包括顶点)有个点.当时,这个图形总的点数为( )
A.8080B.8084C.8088D.8092
11.(本题3分)北京时间2023年10月26日,神舟十七号飞船与中国空间站对接成功,中国空间站距离地球大约为400公里(400000米),请将400000这个数据用科学记数法表示为 .
12.(本题3分)如图所示是一座房子的图片,其中的图形有 .
13.(本题3分)如图,已知是直线上一点,,平分,则 .
14.(本题3分)在一艘轮船上看小岛上的灯塔,若灯塔在轮船的北偏东,则轮船在灯塔的 方向.
15.(本题3分)若,则 .
16.(本题3分)数轴上有三个点A、B、C,数轴的单位长度为1,若点A、B表示的数互为相反数,则图中点C对应的数是 .
17.(本题3分)如图,点在同一条直线上,射线和射线分别平分和,则的余角是 .
18.(本题3分)若,则 .
19.(本题8分)计算
(1); (2).
20.(本题8分)先化简,再求值:,其中,.
21.(本题8分)如图,直线与相交于点F,于点F.
(1)图中与相等的角是 ,与互余的角是 ;
(2)若,求的度数.
22.(本题10分)如图,平面内有,,, 四点,按下列语句画图:
(1)画射线,直线,线段;
(2)延长;
(3)连接与相交于点.
23.(本题10分)补全解题过程.
如图,,,平分,求的度数.
解:,,
,
平分
(依据: ),
,
.
24.(本题10分)阅读材料:我们知道,,类似的,我们把看成一个整体,则.“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把看成一个整体,求将合并的结果.
(2)已知,求代数式的值.
拓广探索:
已知,,,求的值.
25.(本题12分)某登山队队员以大本营为基地,向海拔距离大本营500米的顶峰发起登顶冲击,假设向上走为正,向下走为负,行程记录如下(单位:米),,,,,.
(1)他们有没有登上顶峰?如果没有登上顶峰,他们距离顶峰多少米?
(2)登山时,5名队员在行进中全程均使用了氧气,已知每人每100米消耗氧气升,求5名队员共使用了多少升氧气?
评卷人
得分
一、单选题(共30分)
评卷人
得分
二、填空题(共24分)
评卷人
得分
三、解答题(共66分)
参考答案:
1.A
【分析】本题考查了代数式求值.整体代入是解题的关键.
根据,代值求解即可.
【详解】解:由题意知,,
故选:A.
2.D
【分析】本题主要考查了同类项的定义,代数式求值,解一元一次方程,根据所含字母相同,相同字母指数也相同的单项式叫做同类项得到,据此求出a、b的值,然后代值计算即可.
【详解】解:∵单项式与是同类项,
∴,
∴,
∴,
故选D.
3.A
【分析】本题考查有理数运算的实际应用.根据题意,求出12个月的盈利的和,即可.
【详解】解:由题意,得:万元;
故选A.
4.D
【分析】此题主要考查有理数的大小比较方法,解题关键是先化简再比较.
利用有理数的大小比较方法:正数都大于零,负数都小于零,正数大于负数;两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小;先化简再进一步比较即可.
【详解】解:A、∵,,
∴,故此选项错误;
B、∵,,
∴,故此选项错误;
C、∵,,
∴,故此选项错误;
D、∵负数小于正数,
∴,故此选项正确.
故选D.
5.A
【分析】根据题意列式计算即可.
【详解】解:∵某商品打八折后的售价为160元,
∴该商品的原价为(元),故A正确.
故选:A.
【点睛】本题主要考查了有理数除法的应用,解题的关键是根据题意列出算式.
6.D
【分析】本题主要考查了垂直、角平分线、补角和余角、对顶角等知识,根据角平分线的定义、垂直的定义、对顶角的定义以及补角和余角的定义逐项分析判断即可,熟练掌握角平分线的定义、补角和余角的定义是解题关键.
【详解】解:A. 因为,所以与互为补角,该选项结论正确,不符合题意;
B.因为射线平分,
所以,
又因为,
所以,
所以,即与互为余角,
该选项结论正确,不符合题意;
C.因为,,
所以,
即与互为补角,该选项结论正确,不符合题意;
D. 与为对顶角,该选项结论错误,符合题意.
故选:D.
7.A
【分析】本题考查的是平行线的判定与性质,利用平行线的判定方法与性质逐一分析即可得到答案,熟记平行线的判定方法与平行线的性质是解本题的关键.
【详解】解:∵,(两直线平行,同旁内角互补),故A符合题意;
,(两直线平行,同旁内角互补),故B不符合题意;
,(内错角相等,两直线平行),故C不符合题意;
,(同位角相等,两直线平行),故D不符合题意;
故选A
8.D
【分析】本题主要考查了简单组合体的三视图,掌握主视图、左视图、俯视图分别是从物体的正面、左面、上面看得到的图形成为解题的关键.
根据左视图即从左边观察得到的图形即可解答.
【详解】解:从左边看,可得如图所示几何体的左视图是:
.
故选:D.
9.C
【分析】本题考查了正方体的展开图.熟练掌握正方体展开图“一线不过四,田凹应弃之”(即不能出现同一行有多余4个正方形的情况,不能出现田字形、凹字形的情况)是解题的关键.
根据正方体的展开图的特点进行判断作答即可.
【详解】解:由题意知,从左到右,第1,2,5不属于正方体的表面展开图,第3,4,6属于正方体的表面展开图;
故选:C.
10.C
【分析】本题考查了图形的变化类问题,通过图形的变化,归纳总结,找到规律是解答本题的关键.
根据图形的变化,当时,图形总的点数为:,由此得到答案.
【详解】解:根据题意得:
当时,图形总的点数为:;
当时,图形总的点数为:;
当时,图形总的点数为:;
当时,图形总的点数为:;
当时,图形总的点数为:.
故选:.
11.
【分析】此题考查了科学记数法的表示方法.科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正整数;当原数的绝对值时,n是负整数.
【详解】解:,
故答案为:.
12.三角形、四边形、长方形、正方形、梯形、圆
【分析】根据平面图形的概念求解即可.
【详解】根据题意可得,
其中的图形有三角形、四边形、长方形、正方形、梯形、圆.
故答案为:三角形、四边形、长方形、正方形、梯形、圆.
【点睛】此题考查了简单的平面图形,解题的关键是正确认识常见的平面图形.
13./105度
【分析】本题主要考查了角平分线的定义,几何图形中角的计算,解题的关键是熟练掌握角平分线的定义.
【详解】解:,
,
平分,
,
.
故答案为:.
14.南偏西
【分析】本题考查了方向角,根据题目的已知条件并结合图形求解即可.
【详解】解:如图,灯塔在轮船的北偏东,
轮船在灯塔的南偏西,
故答案为:南偏西.
15.
【分析】本题考查代数式求值,将原式进行变形后代入数值计算即可.
【详解】,
,
故答案为:.
16.2
【分析】本题考查数轴上的点表示数,相反数的定义,正确确定原点是解题关键.首先确定原点位置,进而可得C点对应的数.
【详解】解:∵点A、B表示的数互为相反数,
∴原点在点A、B的正中间,
∴点C对应的数是2.
故答案为:2.
17.和
【分析】本题考查了余角和补角,角平分线,根据角平分线的定义和邻补角的定义即可得出,,从而得出的余角.
【详解】解:∵射线和射线分别平分和,
∴,,
∵,
∴
∴,
∴的余角是和,
故答案为:和.
18.8
【分析】本题主要考查代数式求值,将变形为,然后把整体代入计算求值即可.
【详解】解:∵,
∴,
故答案为:8.
19.(1)
(2)
【分析】本题考查了有理数的混合运算,熟练掌握有理数的运算法则以及运算顺序是解题的关键.
(1)根据有理数加减混合运算法则及顺序进行计算即可;
(2)根据有理数加减混合运算法则及顺序进行计算即可.
【详解】(1)解:
;
(2)解:
.
20.,
【分析】本题主要考查了整式的化简求值,先去括号,然后合并同类项化简,最后代值计算即可.
【详解】解:
,
当,时,原式.
21.(1);
(2).
【分析】本题考查了垂线,余角和补角,对顶角,
(1)根据对顶角相等得出,根据余角的性质得出与互余的角是;
(2)根据邻补角的性质求出的度数,再根据垂线的定义求出的度数,即可求出的度数;
熟练掌握这些知识点是解此题的关键.
【详解】(1)∵和的对顶角,
∴,
∵,
∴,
即,
∴,
即与互余的角是,
故答案为:;
(2)∵,
∴,
∵,
∴,
∴.
22.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据射线,直线,线段的定义画图即可;
(2)根据题意延长
(3)按题目要求标出点E即可.
【详解】(1)解:如图所示,
(2)解:如图所示,
(3)解:如图所示,
23.;100;;角平分线的定义;10.
【分析】本题主要考查了角平分线定义的应用以及角的计算,利用已知和图形,根据交的和差关系恰当填空即可.
【详解】解:,,
,
平分,
(角平分线的定义),
,
,
故答案为:;100;;角平分线的定义;10.
24.(1);(2)8;(3)6
【分析】本题考查了整式的加减运算与化简求值,熟练掌握整体代入思想是解题的关键.
(1)根据合并同类项法则合并即可.
(2)将代数式变形,然后把已知条件的值代入计算即可.
(3)把原式去括号整理后,变为,然后整体代入求值可.
【详解】(1)解:
(2)解:,
,
.
(3)解:,,,
.
25.(1)他们没有登上顶峰,距离顶峰6米
(2)5名队员共使用了15升氧气
【分析】本题考查了有理数混合运算的实际应用;
(1)将所有数据相加,根据结果可知没有登上顶峰,再用500减去所得结果可知他们距离顶峰的距离;
(2)将所有数据的绝对值相加求出每名队员行进的路程,再根据每人每100米消耗氧气升列式计算即可.
【详解】(1)解:(米),
(米),
答:他们没有登上顶峰,距离顶峰6米;
(2)(升),
答:5名队员共使用了15升氧气.
相关试卷
这是一份2023-2024学年华东师大版数学七年级期末考试试题及解析提升卷1,共19页。
这是一份2023-2024学年华东师大版数学七年级期末考试试题及解析提升卷2,共15页。试卷主要包含了已知,,若,则的值为等内容,欢迎下载使用。
这是一份2023-2024学年冀教版数学七年级期末考试试题及解析提升卷2,共19页。试卷主要包含了的相反数是,有理数,,,中,最小的数是,若 ,则式子 的值为,下列说法正确的是等内容,欢迎下载使用。








