初中数学人教版九年级下册27.3 位似优质课件ppt

这是一份初中数学人教版九年级下册27.3 位似优质课件ppt，文件包含273教学课件位似第2课时pptx、273教学设计位似第2课时docx、273预习导学位似第2课时docx、273练习·基础巩固位似第2课时docx、273练习·能力提升位似第2课时docx、273练习·素能拓展位似第2课时docx等6份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

（1）对应角相等，对应边成比例．（2）对应点的连线相交于一点．（3）位似图形的对应顶点到位似中心（在不重合的情况下）的距离之比等于相似比．（4）对应边互相平行或在同一条直线上．
我们知道，在平面直角坐标系中，可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称、旋转（中心对称）等变换，那么，可以用这个方法表示位似变换吗？
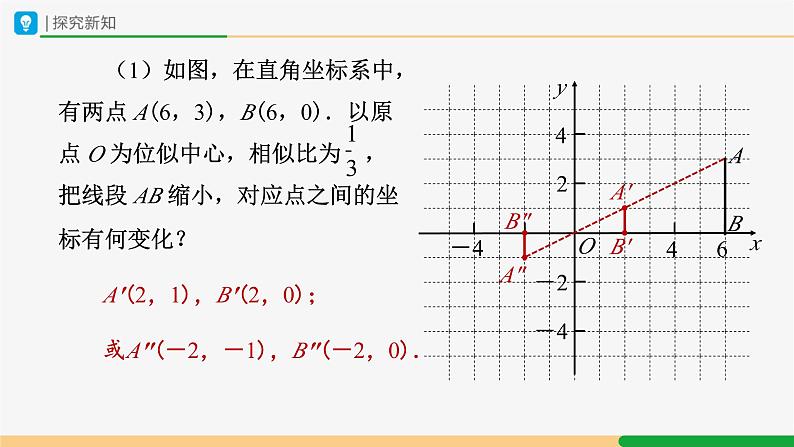
（1）如图，在直角坐标系中，有两点 A(6，3)，B(6，0)．以原点 O 为位似中心，相似比为 ，把线段 AB 缩小，对应点之间的坐标有何变化？
A′(2，1)，B′(2，0)；或A"(－2，－1)，B"(－2，0)．
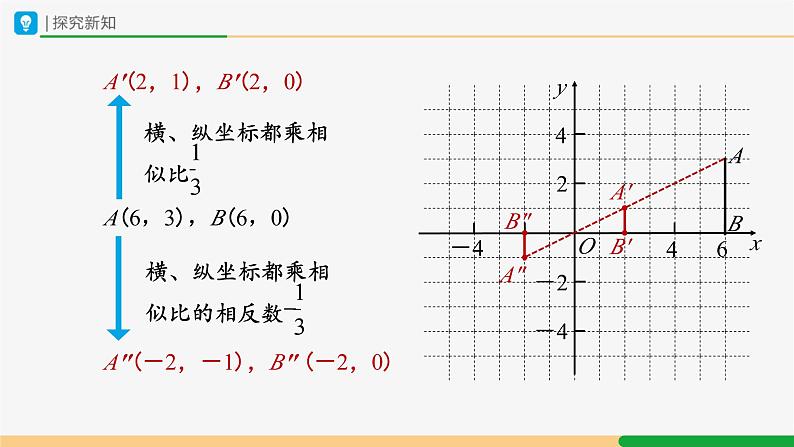
A′(2，1)，B′(2，0)
A″(－2，－1)，B″ (－2，0)
A(6，3)，B(6，0)
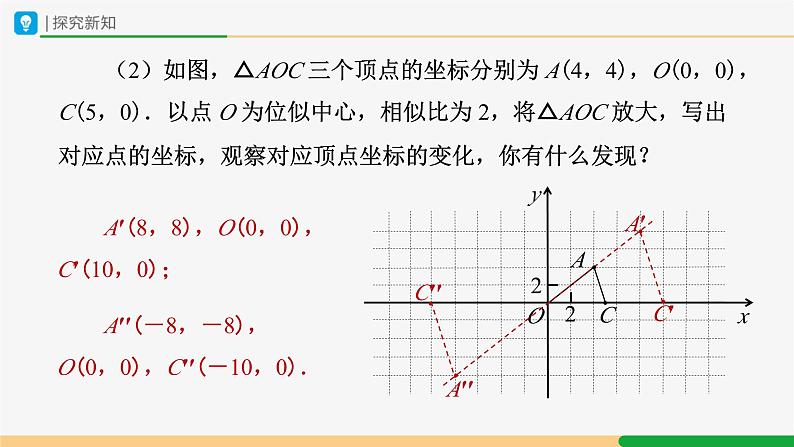
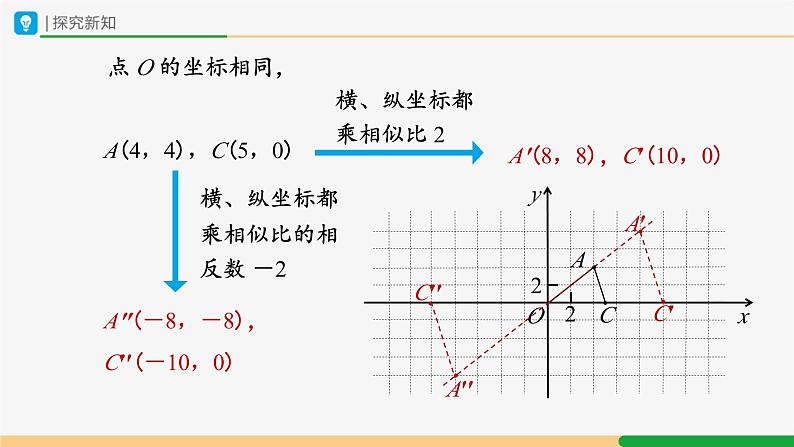
（2）如图，△AOC 三个顶点的坐标分别为 A(4，4)，O(0，0)，C(5，0)．以点 O 为位似中心，相似比为 2，将△AOC 放大，写出对应点的坐标，观察对应顶点坐标的变化，你有什么发现？
A′(8，8)，O(0，0)，C′(10，0)；
A′′(－8，－8)，O(0，0)，C′′(－10，0)．
A′(8，8)，C′(10，0)
A″(－8，－8)，C′′(－10，0)
A(4，4)，C(5，0)
横、纵坐标都乘相似比 2
横、纵坐标都乘相似比的相反数 －2
一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为 k，那么原图形上的点(x，y)对应的位似图形上的点的坐标为(kx，ky)或(－kx，－ky)．用不同方法得到的图形坐标是不同的．
至此，我们已经学习了平移、轴对称、旋转和位似图形的变化方式，你能在下图所示的图案中找到它们吗？
同理，可以找到其他位似图形．
位似变换与其他三种变换有什么联系与区别？
联系：这四种变换都不改变图形的形状，即变换前后得到的图形是相似的．区别：平移、轴对称和旋转都是全等变换，变换前后得到的图形是全等形，而位似变换前后得到的图形一般不是全等的．
例1　如图，△ABO 三个顶点的坐标分别为 A(－2，4)，B(－2，0)，O(0，0)．以原点 O 为位似中心，画出一个三角形，使它与 △ABO 的相似比为 ．
解：如图，利用位似中对应点的坐标的变化规律，分别取点 A′(－3，6)，B′(－3，0)，O(0，0)．顺次连接点 A′，B′，O，
所得△A′B′O 就是要画的一个图形．
还有其他画法吗？自己试一试．
例2　根据不同变换的特点填空．
（1）对于轴对称变换，若以 x 轴为对称轴，则对应点的横坐标______，纵坐标____________；若以 y 轴为对称轴，则对应点的纵坐标_____，横坐标____________．
（2）对于旋转变换，若一个图形绕原点旋转 180°，则旋转前后的两个图形对应点的横坐标与纵坐标_____________．
平面直角坐标系中的位似
平移、轴对称、旋转和位似变换之间的区别与联系
平面直角坐标系中以原点为位似中心的位似图形的画法