第28章 锐角三角函数 人教版数学九年级下册全章复习课件

这是一份第28章 锐角三角函数 人教版数学九年级下册全章复习课件，共20页。
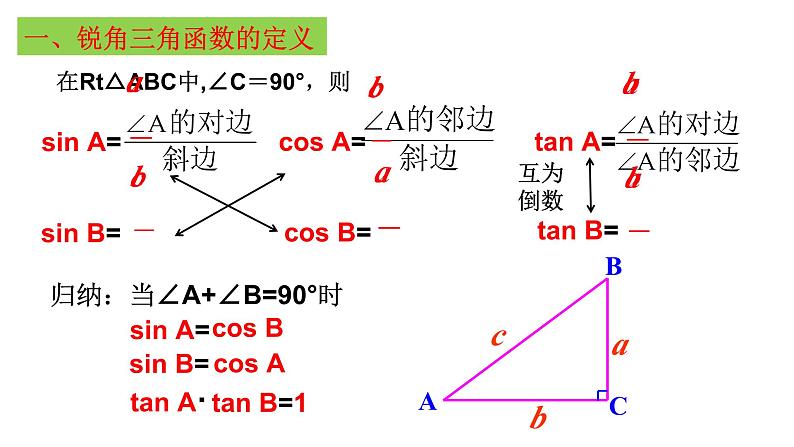
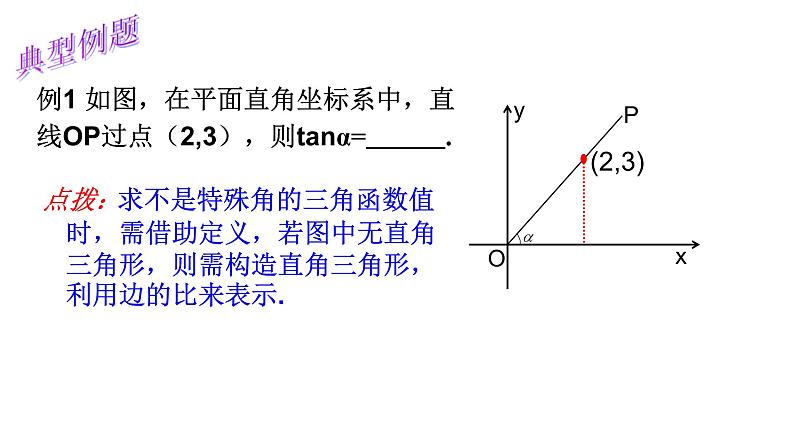
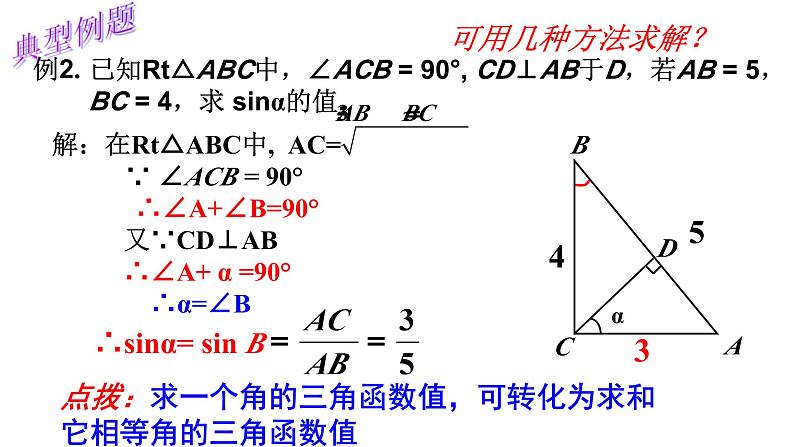
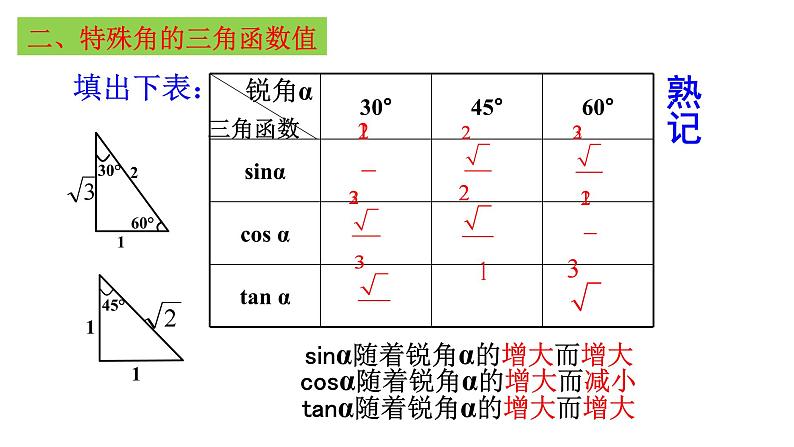
第二十八章 锐角三角函数全章复习本章知识结构梳理锐角三角函数2.30°、45°、60°特殊角的三角函数值。解直角三角形在实际问题中的应用。解直角三角形的依据与一般方法一、锐角三角函数的定义在Rt△ABC中,∠C＝90°，则sin A= cos A= tan A= ∠A的正弦、余弦、正切统称为∠A的锐角三角函数. 对于锐角A的每一个确定的值，sinA都有唯一的值与它对应，所以sinA是∠A的函数，同样地，cosA、tanA也是∠A的函数一、锐角三角函数的定义在Rt△ABC中,∠C＝90°，则sin A= cos A= tan A= sin B= cos B tan B= 归纳：当∠A+∠B=90°时 sin A= cos B= sin B= cos A tan A·tan B=1 互为倒数典型例题例1 如图，在平面直角坐标系中，直线OP过点（2,3），则tanα= .(2,3)点拨： 求不是特殊角的三角函数值时，需借助定义，若图中无直角三角形，则需构造直角三角形，利用边的比来表示.典型例题例2.已知Rt△ABC中，∠ACB = 90°, CD⊥AB于D，若AB = 5，BC = 4，求 sinα的值.∴sinα= sin B453解：在Rt△ABC中, AC= ∵ ∠ACB = 90° ∴∠A+∠B=90°又∵CD⊥AB ∴∠A+ α =90°∴α=∠B点拨：求一个角的三角函数值，可转化为求和它相等角的三角函数值可用几种方法求解？典型例题归纳技巧：例3 如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是______．求一个角的三角函数值①直接法：用定义，有时需作辅助线构造直角三角形。②间接法：转化为求和它相等角的三角函数值。填出下表：二、特殊角的三角函数值熟记sinα随着锐角α的增大而增大tanα随着锐角α的增大而增大cosα随着锐角α的增大而减小锐角α三角函数典型例题=1+例1.计算 2sin30 °+ tan45 º×cos 30°步骤：一“代”二“算”30°22=在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形三、解直角三角形1.什么叫解直角三角形？2.解直角三角形的依据：∠A十∠B＝90° （1）三边关系：（勾股定理）（2）两锐角的关系：（3）边角的关系：归纳：只要知道其中的2个元素（至少有一个是边），就可以求出其余3个未知元素. 三、解直角三角形在Rt△ABC中,∠C=90º，（1）若∠B=38º, AB=20, 求AC. （2）若∠B=38º, AC=10, 求BC和AB. 已知 sin38º≈0.62 cos38º≈0.79 tan38º≈0.78 tan52º≈1.28 有斜用弦无斜用切宁乘勿除取原避中 点拨：当已知和求解中有斜边时，就用正弦或余弦；无斜边时，就用正切；当所求的元素既可用乘法又可用除法时，则用乘法，方便运算；当既可用已知数据又可用中间数据求解时，则用原始数据，尽量避免用中间数据． 四、解直角三角形的应用 因此要掌握直角三角形的一般解法，有时要与方程、全等三角形、相似三角形等知识结合在一起，要注意各种方法的灵活运用。 解直角三角形的知识在解决实际问题中有广泛的应用，如在测量高度、宽度、角度，确定方案时都常用到解直角三角形。解这类题关键是把实际问题转化为数学问题，常通过作辅助线构造直角三角形来解决。知识回顾41.仰角和俯角在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.铅直线水平线视线视线仰角俯角四、解直角三角形的应用概念四、解直角三角形的应用概念2.方位角 指南或指北的方向线与目标方向线构成的角(一般取锐角)，叫做方位角.如图：点A在点O的北偏西30º方向 点B在点O的南偏东45º方向（东南方向）四、解直角三角形的应用概念3.坡角、坡度坡度（坡比）：坡面的铅直高度h和水平宽度l的比叫做坡度，用字母i表示，则坡角：坡面与水平面的夹角叫做坡角hl坡度i与坡角α的关系典型例题 例1. 某学校教学楼靠近一座山坡，坡面AB上方的一块平地BC与地面平行，斜坡AB=40米，坡角∠BAD=60°，为防山体滑坡，学校决定对山坡进行改造．经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B沿BC削进到E处，问BE至少是多少米（结果保留根号）？点拨：题目中没有直角三角形时，我们可以作辅助线构造直角三角形.过点A作AF⊥CB的延长线于点E，则在Rt△ABF中，∠ABF=60° 则在Rt△AEF中，∠AEF=45° ADBECF典型例题典型例题3 例2.海中有一个小岛P，它的周围18海里内有暗礁，渔船跟踪鱼群由西向东航行，在点A测得小岛P在北偏东60°方向上，航行12海里到达B点，这时测得小岛P在北偏东45°方向上．如果渔船不改变航线继续向东航行，有没有触礁危险？请说明理由．ABC60°45°PD例3：如图，直升飞机在高为200米的大楼AB上方P点处，从大楼的顶部和底部测得飞机的仰角为30°和45°，求飞机的高度PO .PBA200米C典型例题解直角三角形的实际应用——常见的基本图形ααββ四、解直角三角形的应用αβ点拨：对于较复杂的图形，需借助桥梁（相等的边、公共边、相等的角）将两个图形联系起来.小结 寄语：数学思想方法是数学的灵魂，本章的学习中运用了数形结合、转化、方程等数学思想方法，希望同学们能熟悉并灵活运用.