





初中数学人教版九年级下册28.1 锐角三角函数教课内容ppt课件
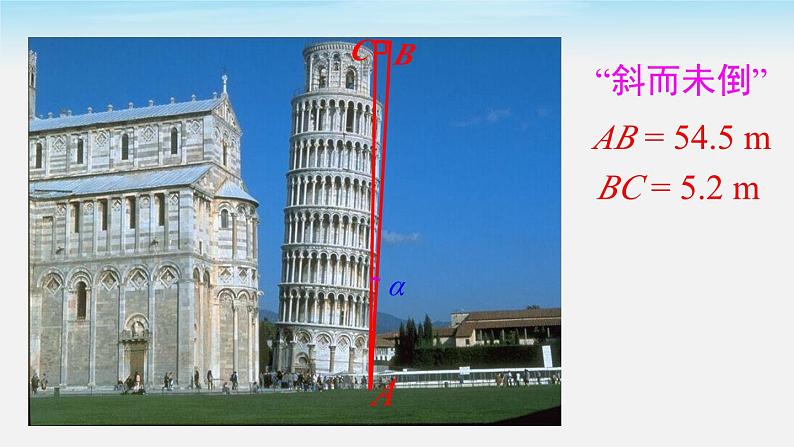
展开比萨斜塔位于意大利中部比萨古城内的教堂广场上,是一组古罗马建筑群中的钟楼.该塔于 1174 年动工兴建,1350 年完工,是 8 层圆柱形建筑,全部用白色大理石砌成,塔高 AB = 54.5 米,塔体总重量达 1.42 万吨.由于地面塌陷,该塔逐渐倾斜,现在塔顶偏离“自然姿势”的水平距离 BC = 5.2 米. 仔细观察下图,你能求出比萨斜塔现在的倾斜角 α 是多少吗?
AB = 54.5 m
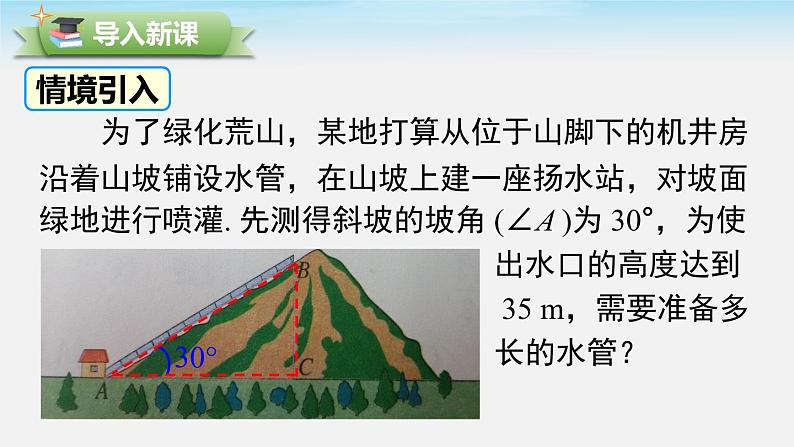
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌. 先测得斜坡的坡角 (∠A )为 30°,为使 出水口的高度达到 35 m,需要准备多 长的水管?
已知直角三角形的边长求正弦值
从上述情境中,你可以发现一个什么数学问题呢?能否结合数学图形把它描述出来?
如图,在 Rt△ABC 中,∠C = 90°,∠A = 30°,BC = 35 m,求 AB.
根据“直角三角形中30°角所对的边等于斜边的一半”,可知∴ AB = 2BC = 2×35 = 70 (m). 故需要准备 70 m 长的水管.
在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
在 Rt△ABC 中,如果∠C = 90°,∠A = 45°, 那么 BC 与 AB 的比是一个定值吗?
解:因为∠A = 45°,∠C = 90°,所以 AC = BC, 由勾股定理,得 AB2 = AC2 + BC2 = 2BC2,
在直角三角形中,如果一个锐角等于 45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于 .
任意画 Rt△ABC 和 Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系?你能解释一下吗?
因为∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC ∽Rt△A'B'C'. 所以
这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与斜边的比也是一个固定值.
如图,在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA,即
例如,当∠A=30° 时,我们有
例 1 如图,在 Rt△ABC 中,∠C = 90°,求 sinA 和sinB 的值.
解:如图①,在 Rt△ABC 中,由勾股定理得
如图②,在 Rt△ABC 中,由勾股定理得
1. 如图,判断对错:
sinA = 0.6 ( )
sinB = 0.8 ( )
2. 在 △ABC中,∠C = 90°,AB = 7,BC = 3,则 sinA 的值为 ( ) A. B. C. D.
例 2 如图,在平面直角坐标系内有一点 P (3,4),连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的正弦值.
解:如图,过点 P 作 PA⊥x 轴于点 A,则点 A (3,0),AP = 4.
在 Rt△APO 中,由勾股定理得
方法总结:在平面直角坐标系求某角的正弦值,一般过已知点向 x 轴或 y 轴引垂线,构造直角三角形,再结合勾股定理求解.
如图,已知点 P 的坐标是 (a,b),则 sinα 等于 ( )
A. B.C. D.
已知锐角的正弦值求直角三角形的边长
提示:已知 sinA 及∠A 的对边 BC 的长度,可以求出斜边 AB 的长,然后再利用勾股定理,求出 AC 的长度,进而求出 sinB 及 Rt△ABC 的面积.
∴ AB = 3BC = 3×3 = 9.
1. 在 Rt△ABC 中,∠C = 90°,sinA = ,BC = 6,则 AB 的长为 ( )
A. 4 B. 6 C. 8 D. 10
2. 在△ABC 中,∠C = 90°,如果 sinA = ,AB = 6, 那么 BC =_____.
例 4 在 △ABC 中,∠C = 90°,AC = 24 cm,sinA = ,求这个三角形的周长.
解:由 sinA = ,设 BC = 7x cm,则 AB = 25x cm.
即 24x = 24,解得 x = 1.
故 BC = 7x = 7 cm,AB = 25x = 25 cm.
∴ △ABC 的周长为 BC+AC+AB = 7+24+25 = 56 (cm).
在 Rt△ABC 中,由勾股定理得
方法总结:已知一边及其邻角的正弦值时,一般需结合方程思想和勾股定理解决问题.
1. 在直角三角形 ABC 中,若三边长都扩大为原来的 2 倍,则锐角 A 的正弦值将 ( ) A. 扩大为原来的 2 倍 B. 不变 C. 缩小为原来的 D. 无法确定扩大还是缩小
2. 如图,在△ABC 中,∠B = 90°,sinA 的值为( )
A. B. C. D.
3. 如图,在正方形网格中有 △ABC,则 sin∠ABC 的值为 .
4. 如图,点 D (0,3),O (0,0),C (4,0) 在 ⊙A 上, BD 是 ⊙A 的一条弦,则 sin∠OBD =_____.
解析:连接 CD,可得出 ∠OBD = ∠OCD,根据点 D (0,3),C(4,0),得 OD = 3,OC = 4,由勾股定理得出 CD = 5,再在直角三角形中求出sin∠OCD 的值即可.
5. 如图,在 △ABC 中, AB = BC = 5,sinA = ,求 △ABC 的面积.
解:作 BD⊥AC 于点 D. ∵ sinA = ,
又∵ AB = AC,BD⊥AC,∴ AC = 2AD = 6,∴ S△ABC = AC·BD÷2 = 12.
解:∵ CD⊥AB,∴∠ADC =∠ACB = 90°. ∴∠ACD = ∠B = 90°-∠A.
6. 如图,在 △ABC 中,∠ACB = 90°,CD⊥AB. (1) sinB 可以用哪两条线段之比表示?
(2) 若 AC = 5,CD = 3,求 sinB 的值.
解: 由 (1) 知,
数学九年级下册28.1 锐角三角函数课文内容课件ppt: 这是一份数学九年级下册28.1 锐角三角函数课文内容课件ppt,共30页。PPT课件主要包含了情景引入,“斜而未倒”,BC52m,情境引入,合作探究,思考1,思考2,典例精析,练一练,A30等内容,欢迎下载使用。
初中人教版28.1 锐角三角函数评课课件ppt: 这是一份初中人教版28.1 锐角三角函数评课课件ppt,共25页。PPT课件主要包含了正弦的定义,知识点1,故AB,你发现了什么,正弦的表示,知识点2,因此sinA,sinB,基础巩固,综合应用等内容,欢迎下载使用。
初中数学人教版九年级下册28.1 锐角三角函数课文内容课件ppt: 这是一份初中数学人教版九年级下册28.1 锐角三角函数课文内容课件ppt,共17页。PPT课件主要包含了“斜而未倒”,BC52m,AB545m,如∠A的正弦,记作sinA,正弦值及其变化规律,小试牛刀,判断对错,想一想,sin∠ACD等内容,欢迎下载使用。













