2023-2024学年甘肃省天水市秦安县九年级（上）期末数学试卷（含解析）

这是一份2023-2024学年甘肃省天水市秦安县九年级（上）期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列各数中，绝对值最大的数是( )
A. −2B. 3C. 0D. −4
2.下列成语中，表示必然事件的是( )
A. 水中捞月B. 守株待兔C. 水涨船高D. 刻舟求剑
3.近年来出生人口持续走低，即使国家开放三胎，也缓解不了颓势，2022年我国出生人口是1062万人，数据1062万用科学记数法表示应为( )
A. 1062×104B. 10.62×106C. 1.062×107D. 0.1062×108
4.4的算术平方根的平方根是( )
A. 2B. −2C. 2D. ± 2
5.下列二次函数的图象通过平移能与二次函数y=x2−2x−1的图象重合的是( )
A. y=2x2−x+1B. y=x2+2x+1
C. y=12x2−2x−1D. y=12x2+2x+1
6.方程x2+2x+1=0的根是( )
A. x1=x2=1B. x1=x2=−1
C. x1=−1，x2=1D. 无实根
7.如图抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1，且图象经过点P(3,0)，则a−b+c的值为( )
A. 0
B. −1
C. 1
D. 3
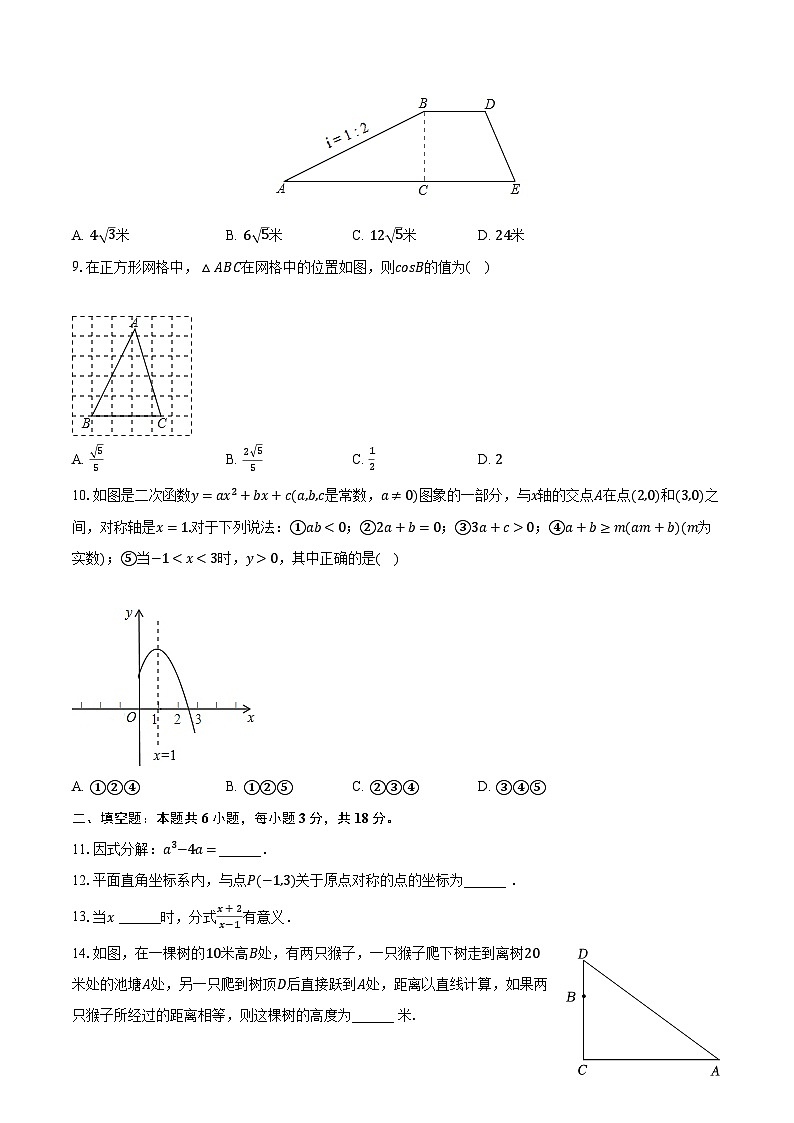
8.如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为( )
A. 4 3米B. 6 5米C. 12 5米D. 24米
9.在正方形网格中，△ABC在网格中的位置如图，则csB的值为( )
A. 55B. 2 55C. 12D. 2
10.如图是二次函数y=ax2+bx+c(a,b,c是常数，a≠0)图象的一部分，与x轴的交点A在点(2,0)和(3,0)之间，对称轴是x=1.对于下列说法：①ab<0；②2a+b=0；③3a+c>0；④a+b≥m(am+b)(m为实数)；⑤当−10，其中正确的是( )
A. ①②④B. ①②⑤C. ②③④D. ③④⑤
二、填空题：本题共6小题，每小题3分，共18分。
11.因式分解：a3−4a=______．
12.平面直角坐标系内，与点P(−1,3)关于原点对称的点的坐标为______ ．
13.当x ______时，分式x+2x−1有意义．
14.如图，在一棵树的10米高B处，有两只猴子，一只猴子爬下树走到离树20米处的池塘A处，另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树的高度为______ 米.
15.如图，设点P在函数y=6x的图象上，PC⊥x轴于点C，交函数y=2x的图象于点A，PD⊥y轴于点D，交函数y=2x的图象于点B，则四边形PAOB的面积为______．
16.若关于x的方程2x+ax+1=1的解是负数，则a的取值范围是______ ．
三、计算题：本大题共1小题，共5分。
17.计算：4sin60°−|−1|+( 3−1)0+ 48
四、解答题：本题共10小题，共91分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题5分)
解方程：2x2−5x+2=0．
19.(本小题8分)
已知|a−2|+ b−3=0，则a2−abb2⋅a2−aba2−b2的值为______ ．
20.(本小题10分)
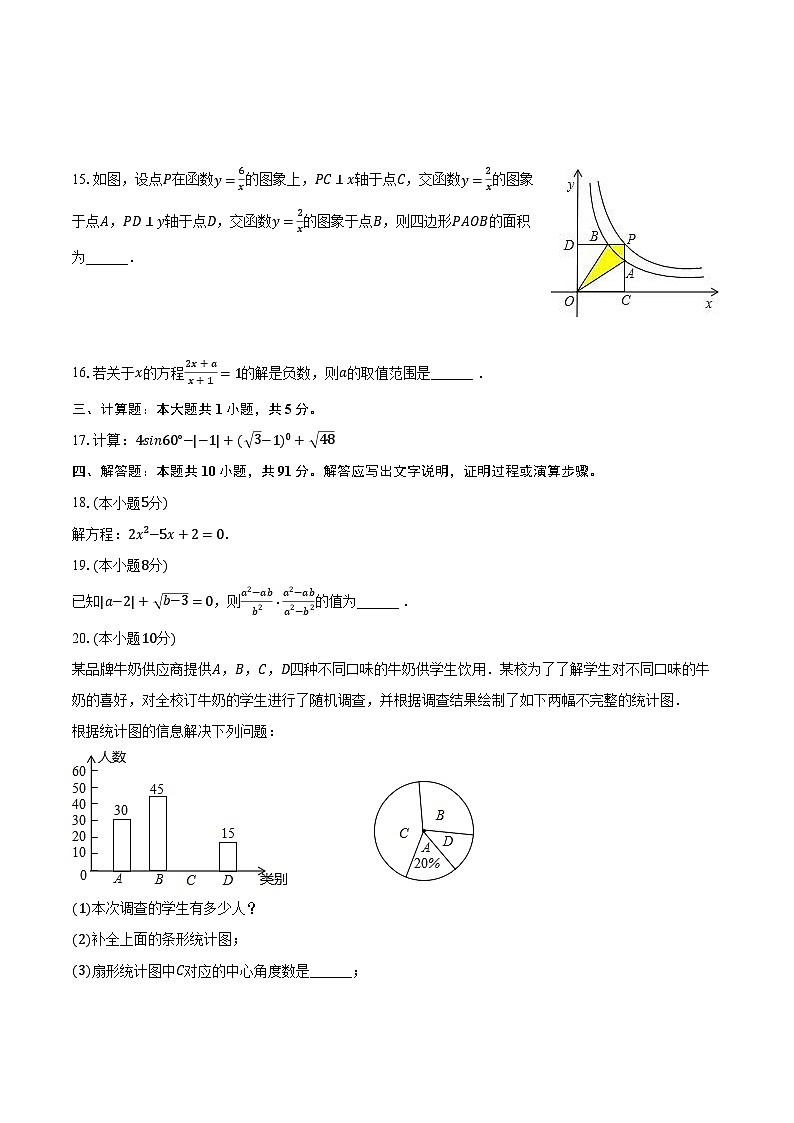
某品牌牛奶供应商提供A，B，C，D四种不同口味的牛奶供学生饮用．某校为了了解学生对不同口味的牛奶的喜好，对全校订牛奶的学生进行了随机调查，并根据调查结果绘制了如下两幅不完整的统计图．
根据统计图的信息解决下列问题：
(1)本次调查的学生有多少人？
(2)补全上面的条形统计图；
(3)扇形统计图中C对应的中心角度数是______；
(4)若该校有600名学生订了该品牌的牛奶，每名学生每天只订一盒牛奶，要使学生能喝到自己喜欢的牛奶，则该牛奶供应商送往该校的牛奶中，A，B口味的牛奶共约多少盒？
21.(本小题8分)
已知m、n是一元二次方程x2−3x−1=0的两个实数根，求下列代数式的值：
(1)(m−n)2；(2)mn+nm．
22.(本小题8分)
一个不透明的口袋里装有分别标有汉字“我”、“爱”、“中”、“国”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先摇均匀．
(1)若从中任取一个球，球上的汉字刚好是“爱”的概率是多少？
(2)从中任取一球，不放回，再从中任取一球，请用树状图或列表的方法，求取出的两个球上的汉字能组成“中国”的概率．
23.(本小题10分)
已知在平面直角坐标系中，一次函数y=x+b的图象与反比例函数y=kx的图象交于点A(1,m)和点B(−2,−1)．
(1)求k、b的值；
(2)连结OA，OB，求△AOB的面积；
(3)结合图象直接写出，当x取何值时，一次函数值大于反比例函数值．
24.(本小题10分)
某商场将每件进价为80元的A商品按每件100元出售，一天可售出128件．经过市场调查，发现这种商品的销售单价每降低1元，其日销量可增加8件．设该商品每件降价x元，商场一天可通过A商品获利润y元．
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)；
(2)A商品销售单价为多少时，该商场每天通过A商品所获的利润最大？
25.(本小题10分)
如图，初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°，已知A点的高度AB为2米，台阶AC的坡度为1： 3(即AB：BC=1： 3)，且B，C，E三点在同一条直线上，请根据以上条件求出树DE的高度．(测量器的高度忽略不计)
26.(本小题10分)
如图所示，在平行四边形ABCD中，∠A=90°，AB=6cm，BC=12cm，点E由点A出发沿AB方向向点B匀速移动，速度为1cm/s，点F由点B出发沿BC方向向点C匀速移动，速度为2cm/s，如果动点E，F同时从A，B两点出发，连接EF，若设运动时间为t s，解答下列问题：
(1)当t为多少时，△BEF为等腰直角三角形；
(2)是否存在某一时刻t，使△EFB∽△FDC？若存在，求出t的值；若不存在，请说明理由．
27.(本小题12分)
如图，在平面直角坐标系中，抛物线y=ax2+bx−2交x轴于A，B两点，交y轴于点C，且OA=2OC=8OB.点P是第三象限内抛物线上的一动点．
(1)求此抛物线的表达式；
(2)若PC/​/AB，求点P的坐标；
(3)连接AC，求△PAC面积的最大值及此时点P的坐标．
答案和解析
1.【答案】D
【解析】解：
依题意，
∵|−2|=2，|3|=3，|0|=0，|−4|=4
∴4>3>2>0
故选：D．
根据绝对值的性质来判断即可，正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值还是0．
本题主要考查绝对值的性质，牢记绝对值的性质是解题的关键
2.【答案】C
【解析】解：A，水中捞月是不可能事件；
B、守株待兔是随机事件；
C、水涨船高是必然事件；
D、刻舟求剑是不可能事件；
故选：C．
根据事件发生的可能性大小判断相应事件的类型．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
3.【答案】C
【解析】解：1062万=10620000=1.062×107．
故选：C．
科学记数法的表现形式为a×10n的形式，其中1≤|a|<10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数．
本题考查了科学记数法的表示方法，科学记数法的表现形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键是要正确确定a的值以及n的值．
4.【答案】D
【解析】解：∵4的算术平方根是2，
∴4的算术平方根的平方根是± 2．
故选：D．
先求出4的算术平方根，再根据平方根定义求出即可．
本题考查了对平方根和算术平方根的应用，主要考查学生的计算能力．
5.【答案】B
【解析】【分析】
主要考查了二次函数图象与几何变换，由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
根据经过平移后能与抛物线y=x2−2x−1重合可知a=1，然后作出选择．
【解答】
解：∵经过平移后能与二次函数y=x2−2x−1的图象重合，
∴a=1，
观察选项，只有选项B符合题意．
故选：B．
6.【答案】B
【解析】解：∵x2+2x+1=0，
∴(x+1)2=0，
则x+1=0，
解得：x1=x2=−1，
故选：B．
由原方程得出(x+1)2=0，开方即可得．
本题主要考查解一元二次方程，解题的关键是熟练掌握完全平方公式及配方法解一元二次方程．
7.【答案】A
【解析】解：∵抛物线y=ax2+bx+c的对称轴为x=1，
∴根据二次函数的对称性得：点(3,0)的对称点为(−1,0)，
∵当x=−1时，y=a−b+c=0，
∴a−b+c的值等于0．
故选：A．
根据二次函数对称性可求出点(3,0)关于对称轴直线x=1的对称点为(−1,0)，然后把(−1,0)代入y=ax2+bx+c即可求出答案．
本题主要考查了二次函数的性质，解答本题的关键是求出点P关于对称轴的对称点，此题难度不大．
8.【答案】B
【解析】解：在Rt△ABC中，
∵i=BCAC=12，AC=12米，
∴BC=6米，
根据勾股定理得：
AB= AC2+BC2=6 5(米)，
故选：B．
先根据坡度的定义得出BC的长，进而利用勾股定理得出AB的长．
此题考查了解直角三角形的应用−坡度坡角问题，勾股定理，难度适中．根据坡度的定义求出BC的长是解题的关键．
9.【答案】A
【解析】【分析】
本题考查了三角函数的定义，求锐角的三角函数值的方法：利用锐角三角函数的定义，转化成直角三角形的边长的比．在直角△ABD中，利用勾股定理即可求得AB的长，然后根据余弦函数的定义即可求解．
【解答】
解：连接AD，
在直角△ABD中，BD=2，AD=4，
则AB= BD2+AD2= 22+42=2 5，
则csB=BDAB=22 5= 55．
故选A．
10.【答案】A
【解析】【分析】
本题主要考查了二次函数图象与系数的关系，关键是熟练掌握①二次项系数a决定抛物线的开口方向，当a>0时，抛物线向上开口；当a<0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时(即ab>0)，对称轴在y轴左；当a与b异号时(即ab<0)，对称轴在y轴右．(简称：左同右异)③常数项c决定抛物线与y轴交点，抛物线与y轴交于(0,c)．
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴判定b与0的关系以及2a+b=0；当x=−1时，y=a−b+c；然后由图象确定当x取何值时，y>0．
【解答】
解：①∵对称轴在y轴右侧，
∴a、b异号，
∴ab<0，故正确；
②∵对称轴x=−b2a=1，
∴2a+b=0；故正确；
③∵2a+b=0，
∴b=−2a，
∵当x=−1时，y=a−b+c<0，
∴a−(−2a)+c=3a+c<0，故错误；
④根据图示知，当x=1时，二次函数有最大值；
此时y=a+b+c，
所以有am2+bm+c≤a+b+c，
所以a+b≥m(am+b)(m为实数)．
故正确．
⑤如图，当−1故错误．
故选：A．
11.【答案】a(a+2)(a−2)
【解析】【分析】
此题主要考查了提取公因式法和公式法分解因式，熟练掌握平方差公式是解题关键．
首先提取公因式a，进而利用平方差公式分解因式得出即可．
【解答】
解：a3−4a=a(a2−4)=a(a+2)(a−2)．
故答案为：a(a+2)(a−2)．
12.【答案】(1,−3)
【解析】解：根据中心对称的性质，得点P(−1,3)关于原点对称点P′的坐标是(1,−3)，
故答案为：(1,−3)．
平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y)，从而可得出答案．
本题主要考查关于原点对称的点坐标的关系，是需要识记的基本问题．记忆方法是结合平面直角坐标系的图形记忆．
13.【答案】≠1
【解析】解：∵分式x+2x−1有意义，
∴x−1≠0，
解得x≠1，
故答案为：≠1．
分式有意义的条件是分母不等于零，据此可得结论．
本题主要考查了分式有意义的条件，解题时也要注意分式无意义的条件是分母等于零．
14.【答案】15
【解析】解：如图，设树的高度为x米，因两只猴子所经过的距离相等都为30米．
由勾股定理得：x2+202=[30−(x−10)]2，解得x=15m．
故这棵树高15m．
根据两只猴子所经过的距离相等，将两只猴子所走的路程表示出来，根据勾股定理列出方程求解．
把实际问题转化为数学模型，构造直角三角形，然后利用勾股定理解决．
15.【答案】4
【解析】解：根据题意，S四边形PCOD=PC⋅PD=6，
S△OBD=S△OAC=12×2=1，
所以，四边形PAOB的面积=S四边形PCOD−S△OBD−S△OAC=6−1−1=4．
故答案为：4
根据反比例函数系数k的几何意义求出四边形PCOD的面积，△OBD和△OAC的面积，然后求解即可．
本题考查了比例系数k的几何意义，过双曲线上的任意一点分别向两条坐标作垂线，与坐标轴围成的矩形面积就等于|k|．
16.【答案】a>1且a≠2
【解析】解：去分母得：2x+a=x+1，
解得：x=1−a，
由解为负数，得到1−a<0，且1−a≠−1，
解得：a>1且a≠2，
故答案为：a>1且a≠2
分式方程去分母转化为整式方程，表示出解，根据解为负数求出a的范围即可．
此题考查了分式方程的解，做题时注意考虑分母不为0．
17.【答案】解：原式=4× 32−1+1+4 3
=2 3+4 3
=6 3．
【解析】本题主要考查实数的运算，解题的关键是掌握特殊锐角三角函数值、绝对值性质、零指数幂、二次根式性质．直接利用特殊锐角三角函数值、绝对值、零指数幂以及二次根式进行运算，再进一步计算可得．
18.【答案】解： 2x2−5x+2=0，
(x−2)(2x−1)=0，
则x−2=0或2x−1=0，
解得x1=2，x2=12．
【解析】利用因式分解法求解即可．
本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
19.【答案】−445
【解析】解：∵|a−2|+ b−3=0，
∴a=2，b=3，
∴a2−abb2⋅a2−aba2−b2=a(a−b)b2⋅a(a−b)(a+b)(a−b)=a2(a−b)b2(a+b)=4×(2−3)9×(2+3)=−445．
故答案为：−445．
根据绝对值和算术平方根的性质求出a，b的值，再把要求的式子进行化简，然后代入进行计算即可．
此题考查了分式的化简求值，用到的知识点是平方差公式、约分，解答此题的关键是求出a，b的值．
20.【答案】(1)本次调查的学生有30÷20%=150人；
(2)C类别人数为150−(30+45+15)=60人，
补全条形图如下：
(3)144°；
(4)600×(45+30150)=300(人)，
答：该牛奶供应商送往该校的牛奶中，A，B口味的牛奶共约300盒．
【解析】解：
(1)见答案；
(2)见答案；
(3)扇形统计图中C对应的中心角度数是360°×60150=144°
故答案为：144°；
(4)见答案．
【分析】
(1)利用A类别人数及其百分比可得总人数；
(2)总人数减去A、B、D类别人数，求得C的人数即可补全图形；
(3)360°×C类别人数所占比例可得；
(4)总人数乘以样本中A、B人数占总人数的比例即可．
本题考查条形统计图、扇形统计图等知识．结合生活实际，绘制条形统计图，扇形统计图或从统计图中获取有用的信息，是近年中考的热点．只要能认真准确读图，并作简单的计算，一般难度不大．
21.【答案】解∵m、n是一元二次方程x2−3x−1=0的两个实数根，
∴m+n=3，mn=−1．
(1)原式=(m+n)2−4mn
=32−4×(−1)
=13；
(2)原式=m2+n2mn
=(m+n)2−2mnmn
=32−2×(−1)−1
=−11．
【解析】(1)(2)先根据根与系数的关系求出m+n和mn的值，然后把所给代数式变形后代入计算即可．
本题考查了一元二次方程根与系数的关系，若x1，x2为方程ax2+bx+c=0(a≠0)的两个根，则x1，x2与系数的关系式：x1+x2=−ba，x1⋅x2=ca．
22.【答案】解：(1)从中任取一个球，球上的汉字刚好是“爱”的概率=14；
(2)画树状图为：

共有12种等可能的结果，其中取出的两个球上的汉字能组成“中国”的结果数为2，
所以取出的两个球上的汉字能组成“中国”的概率=212=16．
【解析】(1)直接利用概率公式求解；
(2)画树状图展示所有12种等可能的结果数，再找出取出的两个球上的汉字能组成“中国”的结果数，然后根据概率公式求解．
本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．掌握概率公式是解题的关键．
23.【答案】解：(1)∵一次函数y=x+b的图象与反比例函数y=kx的图象交于点A(1,m)和点B(−2,−1)．
∴−1=−2+b，−1=k−2
∴b=1，k=2；
(2)∵一次函数y=x+1经过点A(1,m)，
∴m=1+1=2，
∴A(1,2)，
由一次函数y=x+1可知，直线与y轴的交点C为(0,1)，
∴S△AOB=12×1×1+12×1×2=32；
(3)观察图象可知满足条件的x的值：−21．
【解析】(1)把B(−2,−1)分别代入反比例函数y=kx，一次函数y=x+b，即可求得k和b；
(2)求得A的坐标，然后根据三角形的面积公式即可求得．
本题考查了反比例函数与一次函数的交点问题，根据函数的解析式求点的坐标，待定系数法求函数的解析式，三角形面积的求法，熟练掌握待定系数法求函数解析式是解题的关键．
24.【答案】解：(1)由题意得，商品每件降价x元时单价为(100−x)元，销售量为(128+8x)件，
则y=(128+8x)(100−x−80)=−8x2+32x+2560，
即y与x之间的函数解析式是y=−8x2+32x+2560；
(2)∵y=−8x2+32x+2560=−8(x−2)2+2592，
∵−8<0，
∴开口向下，函数有最大值，
∴当x=2时，y取得最大值，此时y=2592，
∴销售单价为：100−2=98(元)，
答：A商品销售单价为98元时，该商场每天通过A商品所获的利润最大．
【解析】本题考查二次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用二次函数的性质解答．
(1)根据题意可以得到y与x的函数关系式；
(2)根据(1)中的函数关系式，然后化为顶点式即可解答本题．
25.【答案】解：∵AF⊥AB，AB⊥BE，DE⊥BE，
∴四边形ABEF为矩形，
∴AF=BE，EF=AB=2
设DE=x，在Rt△CDE中，CE=DEtan∠DCE=DEtan60∘= 33x，
在Rt△ABC中，
∵ABBC=1 3，AB=2，
∴BC=2 3，
在Rt△AFD中，DF=DE−EF=x−2，
∴AF=DFtan∠DAF=x−2tan30∘= 3(x−2)，
∵AF=BE=BC+CE．
∴ 3(x−2)=2 3+ 33x，
解得x=6．
答：树DE的高度为6米．
【解析】由于AF⊥AB，则四边形ABEF为矩形，设DE=x，在Rt△CDE中，CE=DEtan∠DCE=DEtan60∘= 33x，在Rt△ABC中，得到ABBC=1 3，求出BC，在Rt△AFD中，求出AF，由AF=BC+CE即可求出x的长．
本题考查了解直角三角形的应用--仰角、坡度问题、矩形的判定与性质、三角函数；借助仰角构造直角三角形并解直角三角形是解决问题的关键．
26.【答案】解：(1)∵四边形ABCD是平行四边形，∠A=90°，
∴四边形ABCD为矩形，
∴∠B=90°．
当△BEF为等腰直角三角形时，只能是BE=BF，AE=t，则BE=AB−AE=6−t，BF=2t，
∴2t=6−t．
解得：t=2．
∴当t=2时，△BEF为等腰直角三角形．
(2)存在，理由如下：
∵△EFB∽△FDC，
∴EFCF=BFCD．
∵BE=6−t，BF=2t，CF=12−2t，
∴6−t12−2t=2t6．
解得：t=32或t=6．
又∵t=6时，B与E重合，所以不符合，舍去，
综上所述，当t=32时，△EFB∽△FDC．
【解析】(1)由已知条件易证四边形ABCD是矩形，所以∠A=∠B=∠C=90°，若△BEF为等腰直角三角形，则BE=BF，进而可求出t的值；
(2)若△EFB∽△FDC，则BE：CF=BF：DC，结合题目的已知条件可得到关于t的方程，解方程即可得知是否存在t的值．
本题综合考查了和相似三角形有关的问题，用到的知识点有矩形的判定和性质、等腰直角三角形的判定和性质、一元二次方程的运用以及相似三角形的判定和性质，特别是(2)小问得到关于t的一元二次方程是解题关键．
27.【答案】解：(1)抛物线y=ax2+bx−2中c=−2，故OC=2，
而OA=2OC=8OB，则OA=4，OB=12，
故点A、B、C的坐标分别为(−4,0)、(12,0)、(0,−2)，
则y=a(x+4)(x−12)，把C点坐标代入，得：−2=a×4×(−12)，解得：a=1，
故抛物线的表达式为：y=(x+4)(x−12)=x2+72x−2；
(2)抛物线y=x2+72x−2的对称轴为x=−74，
当PC/​/AB时，点P和C的纵坐标相同，
设P(m,−2)
∴0−(−74)=−74−m
∴m=−72
∴点P的坐标为(−72,−2)．
(3)过点P作PH/​/y轴交AC于点H，如图，
设直线AC的表达式为：y=kx+b(k≠0)，
把点A(−4,0)、C(0,−2)的坐标代入，得
0=−4k+b−2=b,
解得：k=−12b=−2,
∴直线AC的表达式为y=−12x−2，
设P(x,x2+72x−2)，则H(x,−12x−2)，
∴PH=−12x−2−(x2+72x−2)=−x2−4x，
则△PAC的面积：
S=S△PHA+S△PHC=12PH·OA=12×4·(−x2−4x)=−2(x+2)2+8，
∵−2<0，
∴S有最大值，当x=−2时，S的最大值为8，
而当x=−2时，y=(−2)2+72×(−2)−2=−5，
∴△PAC面积的最大值为8，此时点P的坐标为(−2,−5)．
【解析】本题考查的是二次函数的综合运用，涉及到一次函数的性质、面积的计算等，有一定的综合性．
(1)抛物线y=ax2+bx−2，则c=−2，故OC=2，而OA=2OC=8OB，则OA=−4，OB=12，确定点A、B、C的坐标，即可求解；
(2)抛物线的对称轴为x=−74，当PC/​/AB时，点P、C的纵坐标相同，利用抛物线的对称性即可求解；
(3)过点P作PH/​/y轴交AC于点H，则△PAC的面积：S=S△PHA+S△PHC=12PH·OA，利用二次函数的性质即可求解．