初中数学华师大版九年级下册27.3 圆中的计算问题第2课时导学案

这是一份初中数学华师大版九年级下册27.3 圆中的计算问题第2课时导学案，共6页。学案主要包含了知识链接，新知预习等内容，欢迎下载使用。

学习目标：
1.体会圆锥侧面积的探索过程.（重点）
2.会求圆锥的侧面积，并能解决一些简单的实际问题.（重点、难点）
自主学习
一、知识链接
1.半径为r,圆心角度数为n°的扇形，其弧长l=__________,扇形面积S=__________.
2.如图，将Rt△ABC绕直角边BC旋转一周，形成的几何体为__________,请画出该几何体的三视图.
思考：圆锥的侧面展开图是什么形状？如何求圆锥的侧面积和全面积呢？
二、新知预习
（预习课本P58-61）填空并完成练习：
1.在图①的方框中，填入对应的名称：

图① 图②
如图②，圆锥底面半径为r,母线长为a,高为h，根据图形，填空：
r,h,a之间满足的数量关系为____________;
圆锥侧面展开图的半径为_____________,弧长为___________;
由S扇形=lr可知，圆锥侧面展开图的面积为•_____•____=_____;
圆锥的全面积为S侧+S底=____________________.
练习：
1.已知圆锥的底面半径为5 cm，母线长为13 cm，则这个圆锥的侧面积是（ ）
A．130π cm2B．120π cm2C．65π cm2D．60π cm2
2.一个圆锥的母线长是3，底面直径是2，则这个圆锥的表面积为（ ）
A．2πB．3πC．4πD．5π
3.圆锥的侧面积为8π，母线长为4，则它的底面半径为（ ）
A．2B．1C．3D．4
合作探究
要点探究
探究点：圆锥的侧面积和全面积
问题1 沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形，这个扇形的弧长与底面的周长有什么关系？
问题2 圆锥侧面展开图是扇形，这个扇形的半径与圆锥中的哪一条线段相等？
【要点归纳】如图，圆锥侧面展开图扇形的半径等于圆锥母线的长l，侧面展开图扇形的弧长等于圆锥的底面周长2πr，因此，圆锥的侧面积为πrl，圆锥的全面积为πr(r+l).
【典例精析】
例1 若将半径为24 cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为（ ）
A．3 cmB．6 cmC．12 cmD．24 cm
【针对训练】一个圆锥的底面半径r＝10，高h＝20，则这个圆锥的侧面积是（ ）
A．100πB．200πC．100πD．200π
例2 小明在手工制作课上，用面积为150π cm2，半径为15 cm的扇形卡纸，围成一个圆锥侧面，求这
个圆锥的底面半径．
【针对训练】圆锥的表面展开图由一个扇形和一个圆组成，已知圆的周长为20π，扇形的圆心角为120°，
求圆锥的全面积.
例3 一个圆锥的高为3cm，侧面展开图是半圆，求：
（1）圆锥母线长与底面半径的比；
圆锥的全面积．
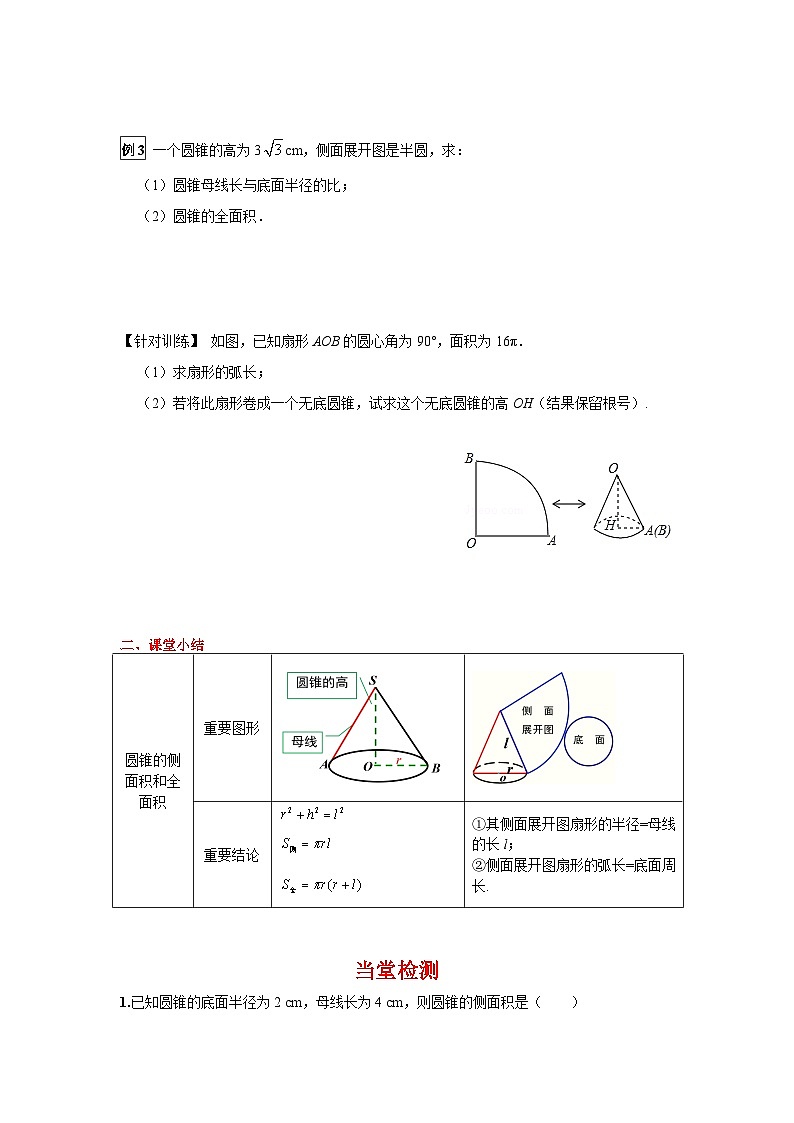
【针对训练】 如图，已知扇形AOB的圆心角为90°，面积为16π．
（1）求扇形的弧长；
（2）若将此扇形卷成一个无底圆锥，试求这个无底圆锥的高OH（结果保留根号）.
二、课堂小结
当堂检测
1.已知圆锥的底面半径为2 cm，母线长为4 cm，则圆锥的侧面积是（ ）
A．10 cm2B．10π cm2C．8 cm2D．8π cm2
2.若用半径为6，圆心角为120°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为（ ）
A．1B．2C．3D．4
3.如果圆锥的母线长为10 cm，高为8 cm，那么它的侧面积等于（ ）
A．80π cm2B．60π cm2C．40π cm2D．30π cm2
4. 某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO＝8米，底面半径OB＝6米，求圆锥的侧面积是________平方米（结果保留π）．
5.已知一个几何体的三视图如图，根据图示的数据计算该几何体的全面积及侧面展开图的圆心角（结果保留π）．
6.如图，蒙古包可近似地看作由圆锥和圆柱组成，现在准备用毛毡搭建一个底面圆面积为25π m2，圆柱高为3 m，圆锥高为2 m的蒙古包，求需要毛毡的面积是多少？
参考答案
自主学习
知识链接
1.
圆锥；画三视图略.
新知预习
1.填空如图所示：
2.（1） （2）a 2πr （3）a 2πr πra （4）πra +πr2
练习：
1.C 2.C 3.A
合作探究
一、要点探究
探究点：圆锥的侧面积和全面积
问题1 解：扇形的弧长与底面圆周长相等.
问题2 解：扇形半径与圆锥的母线长相等.
【典例精析】例1 C 【针对训练】C
例2 解：∵S＝l•R，∴•l•15＝150π，解得l＝20π.设圆锥的底面半径为r，则2π•r＝20π，∴r＝
10 cm．故圆锥底面半径为10 cm．
【针对训练】解：设圆锥的底面圆的半径为r，母线长为l. 根据题意得2πr＝20π，解得r＝10.
20π＝，解得l＝30，所以圆锥的全面积＝π×102+×20π×30＝400π．
例3 解：（1）设圆锥母线长为l，底面圆的半径为r. 根据题意得2πr＝，
所以l＝2r，即圆锥母线长与底面半径的比为2：1.
(2)因为r2+（3）2＝l2，即r2+（3）2＝4r2，解得r＝3，所以l＝6. 所以圆锥的全面积＝π•32+
•2π•3•6＝27π．
【针对训练】解：（1）设扇形的半径是R，则＝16π，解得R＝8，设扇形的弧长是l，则lR＝16π，即4l＝16π，解得l＝4π．故扇形的弧长为4π．
（2）设圆锥的底面圆的半径为r．根据题意得2πr＝4π，解得r＝2，所以这个无底圆锥的高OH＝＝2．
当堂检测
1.D 2.B 3.B 4.60π
5.解：∵由图可知，圆锥的高为4，底面圆的直径为6，半径为3，∴圆锥的母线长为5.∴圆锥的侧面积=πrl＝π×3×5＝15π，底面圆的面积=πr2＝9π，∴该几何体的表面积为24π．
侧面展开扇形的弧长为6π，所以侧面展开图所对的圆心角度数为＝216°.
6.解：设底面圆的半径为R，则πR2＝25π，解得R＝5. 由勾股定理得圆锥的母线长＝＝（m），所以圆锥的侧面积＝×2π×5×＝5π(m2).圆柱的侧面积＝2π×5×3＝30π(m2)，所以需要毛毡的面积为（30π+5π）m2．
圆锥的侧面积和全面积
重要图形

重要结论
①其侧面展开图扇形的半径=母线的长l；
②侧面展开图扇形的弧长=底面周长.