期末经典题型练习（一）2023-2024学年九年级上册苏科版（含解析）

这是一份期末经典题型练习（一）2023-2024学年九年级上册苏科版（含解析），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．一个不透明的袋子中装有3个白球，2个黑球，它们除了颜色外都相同．将球摇匀后，从中随机摸出一个球，记下颜色后放回，再随机摸出一个球．两次摸到的球颜色相同的概率是（ ）
A．B．C．D．
2．某校举行学生会成员的竞选活动，对竞选者从民主测评和演讲两个方面进行考核，两项成绩均按百分制计，规定民主测评的成绩占40%，演讲的成绩占60%，小新同学的民主测评和演讲的成绩分别为80分和90分，则他的最终成绩是（ ）
A．83分B．84分C．85分D．86分
3．一元二次方程化为一般形式后，常数项为（ ）．
A．6B．C．1D．
4．若a为方程的解，则的值为（ ）
A．4B．2C．－4D．－12
5．下列语句中，正确的是（ ）
A．任何一个圆都只有一个圆内接三角形
B．钝角三角形的外心在三角形内部
C．三角形的外心是到三角形三边的距离相等的交点
D．三角形的外心是三角形三边垂直平分线交点
6．如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面圆的半径为（ ）cm．
A．15B．30C．45D．30π
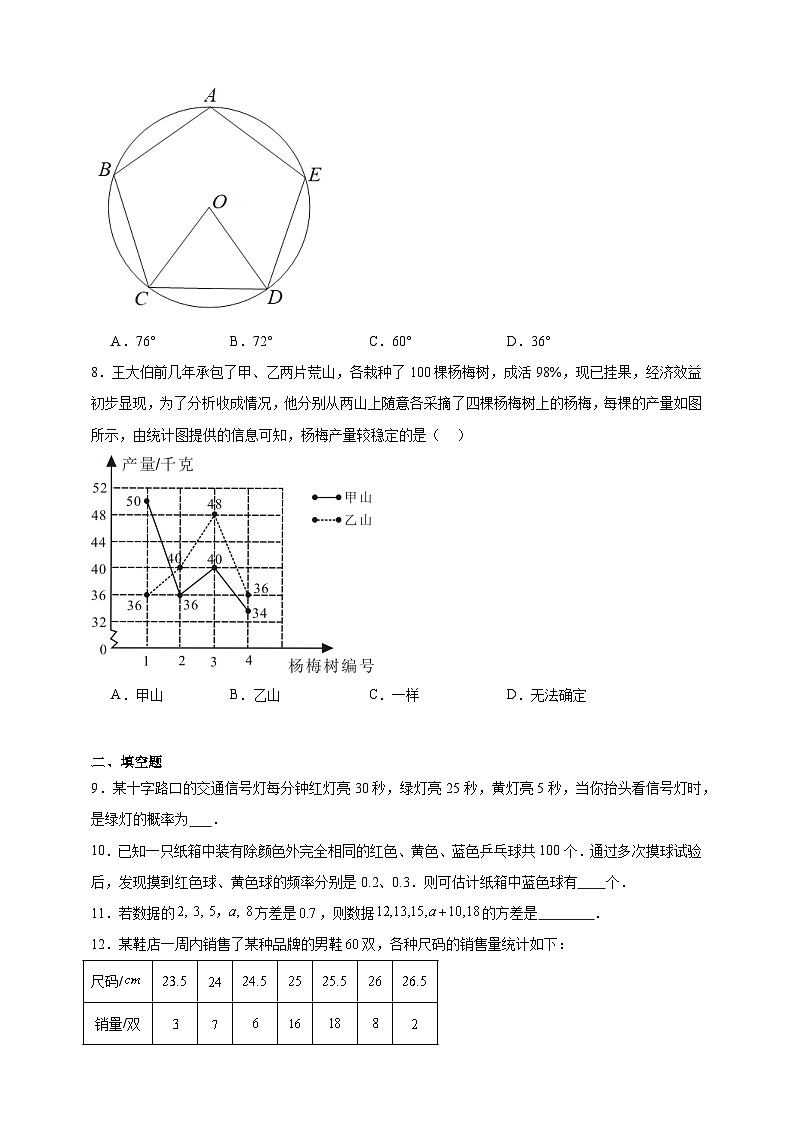
7．如图，正五边形ABCDE内接于⊙O，则正五边形中心角∠COD的度数是（ ）
A．76°B．72°C．60°D．36°
8．王大伯前几年承包了甲、乙两片荒山，各栽种了100棵杨梅树，成活98%，现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了四棵杨梅树上的杨梅，每棵的产量如图所示，由统计图提供的信息可知，杨梅产量较稳定的是（ ）
A．甲山B．乙山C．一样D．无法确定
二、填空题
9．某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为 ．
10．已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个．通过多次摸球试验后，发现摸到红色球、黄色球的频率分别是0.2、0.3．则可估计纸箱中蓝色球有 个．
11．若数据的方差是，则数据的方差是 ．
12．某鞋店一周内销售了某种品牌的男鞋双，各种尺码的销售量统计如下：
由此你能给这家鞋店提供的进货建议是 .
13．若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根，则这个直角三角形斜边的长是 ．
14．如图，在矩形ABCD中，AB＝5，BC＝7，点E为BC上一动点，把△ABE沿AE折叠当点B的对应点落在∠ADC的角平分线上时，则点到BC的距离为 ．
15．在一元二次方程中，若，则称a是该方程的中点值．
（1）方程的中点值是 ；
（2）已知的中点值是3，其中一个根是2，则此时mn的值为 ．
16．已知点、、、在圆上，且切圆于点，于点，对于下列说法：①圆上是优弧；②圆上是优弧；③线段是弦；④和都是圆周角；⑤是圆心角，其中正确的说法是 ．
17．如图，在平面直角坐标系中，点，，的横、纵坐标都为整数，过这三个点作一条圆弧，则此圆弧的圆心坐标为 ．
18．如图，在⊙O中，AC＝BD，若∠AOC＝120°，则∠BOD＝ ．
三、解答题
19．关于x的方程有且只有一个实数解，求k.
20．如图，要建一个面积为140平方米的仓库，仓库的一边靠墙，这堵墙的长为18米，在与墙垂直的一边要开一扇2米宽的门．已知围建仓库的现有木板材料可使新建板墙的总长为32米，那么这个仓库的宽和长分别为多少米？
21．如图是两个自由转动的转盘，盘A被分成四等份，分别标有1，2，3，4四个数字，转盘B被分成三等份，分别标有5，6，7三个数字．小王和小李用这两个转盘做游戏，若两个转盘转出的数字之积为奇数，则小王胜，若两个转盘转出的数字之积为偶数，则小李胜．（如果指针恰好指在分界线上，就得重转，直到指针指向某一数字为止．）

(1)请用树状图或列表法，分别求出小王和小李获胜的概率；
(2)这个游戏规则公平吗?如果不公平，请你设计一个公平合理的游戏规则．
22．某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数;(2)写出甲、乙测验成绩的中位数;
(3)计算甲、乙测验成绩的方差;(保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
23．如图，已知等边的边长为6，以为直径的与边，分别交于D，E两点，连结，．
（1）求的度数．
（2）求劣弧的长．
24．已知是的直径，是的切线，是切点，与交于点．
（1）如图1，若，求的度数；
（2）如图2，若为的中点，求证：直线是的切线．
参考答案：
1．B
【分析】先画出树状图得到所有等可能的结果数，再由概率公式即可求出两次摸出的球颜色相同的概率．
【详解】解：画树状图如图：
共有25种等可能的结果，两次摸出的球颜色相同有13种情况，
则两次摸出的球颜色相同的概率为，
故选：B．
【点睛】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率所求情况数与总情况数之比．
2．D
【分析】根据加权平均数的定义列式计算即可．
【详解】解：他的最终成绩为（分，
故选：．
【点睛】本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
3．B
【分析】方程整理为一般形式，找出常数项即可．
【详解】解：方程整理得：，则常数项为−6，
故选：B．
【点睛】此题考查了一元二次方程的一般形式，一元二次方程的一般形式是：（a，b，c是常数且a≠0），在一般形式中叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
4．A
【分析】将代入方程可得，再将其作为整体代入求值即可得．
【详解】解：由题意，将代入方程得：，即，
则
故选：A．
【点睛】本题考查了一元二次方程的解、代数式求值，熟练掌握整体思想是解题关键．
5．D
【分析】根据确定圆的条件、三角形外接圆的性质以及外心的定义分析得出即可．
【详解】A、任何一个圆有无数个圆内接三角形，故本选项不符合题意；
B、钝角三角形的外心在三角形外部，故本选项不符合题意；
C、三角形的外心是三角形三边垂直平分线的交点，故本选项不符合题意；
D、三角形的外心是三角形三边垂直平分线交点，故本选项符合题意；
故选：D．
【点睛】本题考查了三角形的外心的定义、确定圆的条件、外心的性质，熟记外心的性质是解题的关键．
6．A
【分析】作出等腰三角形底边上的高线OE，首先根据直角三角形30°所对的直角边等于斜边的一半求出等腰三角形底边上的高线OE的长度，即得到扇形OCD所在的圆的半径R，然后根据弧长公式求出的长度，的长度即为圆锥底面圆的周长，最后根据周长求出半径即可．
【详解】如图，过点O作OE⊥AB，垂足为E，
∵△OAB为顶角为120°的等腰三角形，
∴=30°，cm，
∴cm，
设圆锥的底面圆半径为rcm，根据题意得，
，
解得，
所以该圆锥的底面圆的半径为15cm，
故选A．
【点睛】本题考查了直角三角形30°所对的直角边等于斜边的一半、扇形的弧长公式、圆的周长公式，准确将扇形的弧长转化为底面圆的周长是解决本题的关键．
7．B
【分析】根据正多边形的中心角的计算公式：计算即可．
【详解】解：∵五边形ABCDE是⊙O的内接正五边形，
∴五边形ABCDE的中心角∠COD的度数为=72°，
故选：B．
【点睛】本题考查的是正多边形和圆，掌握正多边形的中心角的计算公式：是解题的关键．
8．B
【分析】根据平均数的求法求出平均数，再求出两组数据的方差，再比较即可解答．
【详解】解：根据题意得：甲山四颗杨梅产量的平均数为：
千克，
乙山四颗杨梅产量的平均数为：
千克，
∴ ，
，
∴ ，
∴乙山上的杨梅产量较稳定．
故选：B
【点睛】本题考查了折线统计图、平均数与方差的意义，熟练掌握方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定是解题的关键．
9．
【分析】随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数，据此用绿灯亮的时间除以三种灯亮的总时间，求出抬头看信号灯时，是绿灯的概率为多少即可．
【详解】抬头看信号灯时，是绿灯的概率为．
故答案为．
【点睛】此题主要考查了概率公式的应用，要熟练掌握，解答此题的关键是要明确：（1）随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数．（2）P（必然事件）=1．（3）P（不可能事件）=0．
10．50.
【分析】蓝色球的个数等于总个数乘以摸到蓝色球的概率即可
【详解】由已知得纸箱中蓝色球的个数为:
100×(1-0.2-0.3)=50(个)
故答案为:50
【点睛】此题考查概率公式，难度不大
11．0.7
【分析】根据方差的意义与求法将第一组数据中的的值求出来,再代入第二组数据求方差即可.但仔细观察可以发现,第二组数据每一个数都是在第一组数据的基础上加10,其波动情况并没有发生变化,故方差没有变化,也是0.7.
【详解】解:根据方差的意义,第二组数据每一个数都是在第一组数据基础上加了10,波动情况没有发生变化,故其方差也为0.7.
故答案为:0.7.
【点睛】本题主要考查了方差的意义,深刻理解其意义是解答关键.
12．25.5cm尺码的鞋子可以多进一些（答案不唯一，符合实情就行）
【分析】利用众数的意义进行解答即可.
【详解】解：去鞋厂进货时25.5cm尺码型号的鞋子可以多进一些，这组数据中的众数是25.5，故男鞋中型号25.5cm尺码销售较好，25.5cm尺码的鞋子可以多进一些.
故答案为：25.5cm尺码的鞋子可以多进一些. （答案不唯一，符合实情就行）
【点睛】本题题主要考查了众数的意义，理解众数反映了一组数据的集中程度，是描述一组数据集中趋势的量是解答本题的关键.
13．
【分析】由题意解一元二次方程得到或，再根据勾股定理得到直角三角形斜边的长是．
【详解】解：一个直角三角形两条直角边的长分别是一元二次方程的两个实数根，
由公式法解一元二次方程可得，
根据勾股定理可得直角三角形斜边的长是，
故答案为：．
【点睛】本题考查勾股定理求线段长，根据题意解出一元二次方程的两根是解决问题的关键．
14．2或1/1或2
【分析】连接，过点作于M．设，则AM=7-x，根据等腰直角三角形的性质和折叠的性质得到：（7-x）2=25-x2，通过解方程求得x的值，易得点到BC的距离．
【详解】解： 矩形ABCD，

连接，过点作于M．
∵点B的对应点落在∠ADC的角平分线上，


∴设，则AM=7-x， 又由折叠的性质知，
∴在直角中，
由勾股定理得到：，即（7-x）2=25-x2，
解得：x1=3，x2=4，
则点到BC的距离为5-3=2或5-4=1．
故答案为：2或1．
【点睛】本题考查的是翻折变换的性质，掌握翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．
15． 4 48
【分析】（1）利用中点值的定义进行分析即可；
（2）利用中点值的定义求出的值，将的值与方程的根代入方程即可求出，从而计算的值．
【详解】解：（1）由，得，
，
该方程的中点値为．
（2）由，得，
该方程的中点值为，
，解得．
的一个根是，
，即，
解得．
符合题意．
．
故答案为：；．
【点睛】本题考查了新定义概念，解决本题的关键是充分理解新定义的含义．
16．①②③⑤
【分析】根据优弧的定义，弦的定义，圆周角的定义，圆心角的定义逐项分析判断即可
【详解】解：，都是大于半圆的弧，故①②正确，
在圆上，则线段是弦；故③正确；
都在圆上，
是圆周角
而点不在圆上，则不是圆周角
故④不正确；
是圆心，在圆上
是圆心角
故⑤正确
故正确的有：①②③⑤
故答案为：①②③⑤
【点睛】本题考查了优弧的定义，弦的定义，圆周角的定义，圆心角的定义，理解定义是解题的关键．优弧是大于半圆的弧，任意圆上两点的连线是弦，顶点在圆上，并且两边都和圆相交的角叫做圆周角，顶点在圆心，并且两边都和圆相交的角叫做圆心角．
17．（2，1）
【分析】根据垂径定理的推论：弦的垂直平分线必过圆心，可以作弦AB和BC的垂直平分线，交点即为圆心．
【详解】解：根据垂径定理的推论：弦的垂直平分线必过圆心，
可以作弦AB和BC的垂直平分线，交点即为圆心．
如图所示，则圆心是（2，1）．
故答案为（2，1）．
【点睛】本题考查垂径定理的应用，解答此题的关键是熟知垂径定理，即“垂直于弦的直径平分弦”．
18．/120度
【分析】根据圆的性质，可得OA=OB，OC=OD，证明△AOC≌△BOD，即可得答案．
【详解】解：由题意可知：OA=OB，OC=OD，
∵AC＝BD，
∴△AOC≌△BOD，
∵∠AOC＝120°，
∴∠BOD＝120°，
故答案为：120°．
【点睛】本题考查了圆的性质、三角形全等的判定和性质，做题的关键是证明△AOC≌△BOD．
19．4或或0
【分析】分k=0和k≠0求解，当k≠0时，再分方程是一元二次方程和不是一元二次方程两种情况求解．
【详解】当k=0时，方程变形为，整理，得4x+1=0，
方程只有一个实数解，符合题意，
当k≠0时，方程两边用时乘以x(x-1)，
整理，得，
当k=4时，方程变形为3x+1=0，
方程只有一个实数解，符合题意，
当k≠4时，方程只有一个实数根，
所以，
解得k=，
综上所述，当方程只有一个实数解，符合题意的k值为4或或0．
【点睛】本题考查了分式方程的解法，分式方程转化为一元一次方程或一元二次方程，正确进行分类是解题的关键．
20．这个仓库的长和宽分别为14米、10米
【分析】首先设这个仓库的长为x米，则宽表示为（32+2-x），再根据面积为140平方米的仓库可得x×（32+2-x）=140，再解一元二次方程即可．
【详解】解：设这个仓库的长为x米，由题意得：x×（32+2-x）=140，
解得：x1=20，x2=14，
∵这堵墙的长为18米，
∴x=20不合题意舍去，
∴x=14，
宽为：×（32+2-14）=10（米）．
答：这个仓库的长和宽分别为14米、10米．
【点睛】此题主要考查了一元二次方程的应用，关键是正确理解题意，正确表示出长方形的长和宽．
21．(1)小王胜的概率，小李胜的概率，
(2)不公平，理由见详解
【分析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；
（2）因为小王胜的概率，小李胜的概率，可判断所以这个游戏不公平．设计对游戏双方公平的游戏规则只要他们获胜的概率相等即可．
【详解】（1）画树状图如下：

共有12种等可能的结果，其中奇数有4种可能，偶数有8种可能；
小李胜：胜两个数字的积为偶数的概率是：．
小王胜：两个数字的积为奇数的概率是：．
（2）这个游戏不公平，理由如下：
小王胜的概率，小李胜的概率，
则，
所以这个游戏不公平．
对游戏双方公平的游戏规则可为：若转出的两数之积为3的倍数，小王胜；否则小李胜，．
【点睛】本题考查了游戏公平性：先利用列表法或树状图法展示所有等可能的结果数，然后根据概率的概念分别计算出游戏双方获胜的概率，再比较大小进行判断．也考查了利用列表法或树状图法求概率．
22．(1)=80(分)，=80(分)；(2)80(分)，80(分)；(3)≈9.33，≈11.33；（4）应该派甲去参赛，理由见解析．
【分析】（1）由平均数的计算公式计算甲、乙测试成绩的平均分；
（2）将一组数据从小到大（或从大到小）重新排列后，中间两个数的平均数是甲、乙测试成绩的中位数；
（3）由方差的计算公式计算甲、乙测试成绩的方差；
（4）方差越小，表明这个同学的成绩偏离平均数越小，即波动越小，成绩越稳定．
【详解】(1)= =80(分)，==80(分)．
(2)甲测验成绩的中位数是=80(分)，乙测验成绩的中位数是=80(分)．
(3) =[(79-80)2+(78-80)2+(84-80)2+(81-80)2+(83-80)2+(79-80)2]≈9.33，= [(83-80)2+(77-80)2+(80-80)2+(85-80)2+(80-80)2+(75-80)2]≈11.33．
(4)应该派甲去参赛．理由：因为甲、乙测验成绩的平均数和中位数相同，但甲的方差小，所以甲的测验成绩更稳定，应该派甲去参赛．
【点睛】本题考查了平均数，中位数，方差的意义．平均数表示一组数据的平均程度．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量．
23．（1）；（2）劣弧的长为
【分析】（1）由题意易得，，然后问题可求解；
（2）根据弧长计算公式可直接进行求解．
【详解】解：（1）∵是等边三角形，
∴，
∵，
∴，
∴△AOD、△OBE都为等边三角形，
∴，
∴；
（2）由（1）及弧长计算公式可得：
．
【点睛】本题主要考查弧长计算公式，熟练掌握弧长计算公式是解题的关键．
24．（1）55°；（2）见解析
【分析】（1）根据AP是⊙O的切线，可得∠BAP=90°，∠P=35°，即可求得∠ABP的度数；
（2）连接AC，OC，根据AB是⊙O的直径，可得∠ACB=∠ACP=90°，再根据D为AP的中点，得DC=AD=DP，∠DAC=∠DCA，进而可以证明直线CD是⊙O的切线．
【详解】解：（1）是的直径，是的切线，
，
；
．
（2）如图，连接AC，OC，
∵AB是⊙O的直径，
∴∠ACB=∠ACP=90°，
∵D为AP的中点，
∴DC=AD=DP，
∴∠DAC=∠DCA，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠OAC+∠DAC=∠OCA+∠DCA，
∵∠OAC+∠DAC=∠BAP=90°，
∴∠OCA+∠DCA=∠OCD=90°．
∵OC是半径，
∴直线CD是⊙O的切线．
【点睛】本题考查了切线的判定与性质、圆周角定理，解决本题的关键是掌握切线的判定与性质．
尺码/
销量/双
次数
1
2
3
4
5
6
甲
79
78
84
81
83
75
乙
83
77
80
85
80
75