数学人教版5.3.2 命题、定理、证明教学演示ppt课件

这是一份数学人教版5.3.2 命题、定理、证明教学演示ppt课件，共25页。PPT课件主要包含了如延长线段AB，命题的形式，如果那么，命题的组成，题设是已知事项，题设成立，结论一定成立，真命题，不能保证结论一定成立，假命题等内容，欢迎下载使用。
我们日常讲话中，有些话是对某件事情作出判断的，而有些话只是对事物进行描述的.
鄱阳湖是中国最大的淡水湖.
在几何中，同样有判断和描述这两类语言，如：
①两条直线相交，只有一个交点.
②画线段AB=3cm.
探究点1 命题及其构成
判断一件事情的语句，叫做命题．
1.只要对一件事情作出了判断，不管正确与否，都是命题.
如：相等的角是对顶角.
2.如果一个句子没有对某一件事情作出任何判断，那么它就不是命题.
思考：下列语句中，哪些是命题，哪些不是命题?（1）两直线平行，同位角相等.（2）正数大于负数.（3）同角的余角相等.（4）两直线平行，同旁内角相等.（5）对顶角相等.（6）在直线AB上任取一点C.（7）明天会下雨吗?（8）画线段AB=CD.（9）相等的角都是直角.（10）同旁内角互补.
一个词语、疑问句、感叹句、祈使句以及表示画图的语句都不是命题.
①如果两条直线都与第三条直线平行，那么这两条直线也互相平行；②如果两个数的绝对值相等，那么这两个数也相等.③如果一个数的平方等于9，那么这个数是3.
观察下列命题，你能发现这些命题有什么共同的结构特征？
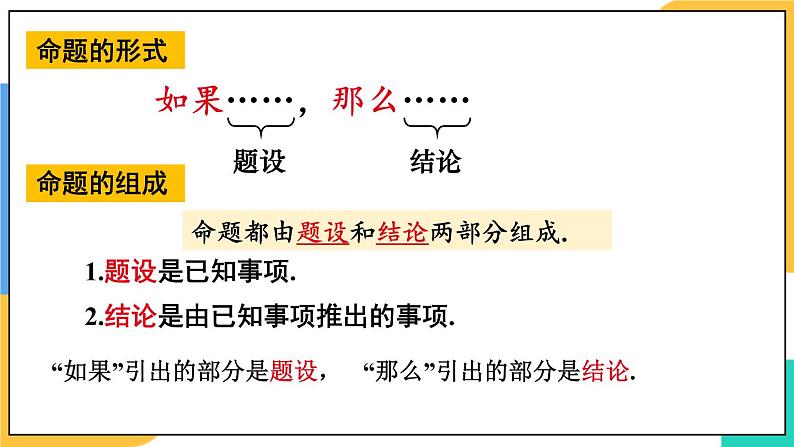
都是“如果……那么……”的形式.
命题都由题设和结论两部分组成.
2.结论是由已知事项推出的事项.
“如果”引出的部分是题设，
“那么”引出的部分是结论.
指出下列命题的题设、结论，并改写成“如果……那么……”的形式．
①两条平行线被第三条直线所截，同旁内角互补；②对顶角相等；③等式两边加同一个数，结果仍是等式.
如果两条平行线被第三条直线所截，那么同旁内角互补.
如果两个角是对顶角，那么这两个角相等.
如果在等式的两边加同一个数，那么结果仍是等式.
1.下列语句是命题的是( ).A.连接A，B 两点B.用三角板画∠AOB=30°C.两点之间，线段最短D.两直线相交有几个交点?
2.指出下列命题的题设和结论：（1）如果AB⊥CD，垂足为O，那么∠AOC=90°；（2）如果∠1=∠2，∠2=∠3，那么∠1=∠3；（3）两直线平行，同位角相等.
【选自教材第21页 练习 第1题】
问题1：他们是不是命题？
问题2：指出上述命题的题设和结论.
观察下列语句，回答问题．
问题3：判断上述命题是否正确？如果错误，为什么？
①如果两条直线相交，那么它们只有一个交点；②同旁内角互补，两直线平行；③相等的两个角是对顶角；④任意两个直角都相等.
探究点2 真命题与假命题
思考：下列命题哪些是真命题? 哪些是假命题?（1）在同一平面内，如果一条直线垂直于两条平行线中的一条，那么也垂直于另一条；（2）如果两个角互补，那么它们是邻补角；（3）如果 | a | = | b |，那么 a = b ；（4）经过直线外一点有且只有一条直线与这条直线平行；（5）两点确定一条直线．
思考：如何判定一个命题是假命题?
例如，要判定命题 “相等的角是对顶角” 是假命题， 可以举出如下反例：
如图：OC是∠AOB的平分钱， ∠1=∠2， 但它们不是对顶角．
判断一个命题是假命题，只要举出一个例子(反例)，它符合命题的题设，但不满足结论就可以了.
1.举出学过的2～3个真命题.
【选自教材第21页 练习 第2题】
2.命题“同位角相等”是真命题吗?如果是，说出理由；如果不是，请举出反例.
【选自教材第22页 练习 第2题】
2.如图：∠1和∠2是同位角， 但它们不相等．
在很多情况下，一个命题的正确性需要经过推理，才能作出判断，这个推理过程叫做证明.
证明中的每一步推理都要有根据，不能“想当然”.这些根据，可以是已知条件，也可以是学过的定义、基本事实等.
探究点3 定理与证明
例1 如图，已知直线 b∥c，a⊥b. 求证a⊥c.
证明：∵ a⊥b（已知），
∴∠1=90º （垂直的定义）.
又∵ b∥c（已知），
∴∠1=∠2（两直线平行，同位角相等）.
∴∠2=∠1=90º（等量代换）.
∴ a⊥c（垂直的定义）.
由此，我们归纳出几何证明的一般步骤：
②根据命题的题设和结论，结合图形，写出已知、求证；
③通过分析，找出证明的方法，写出证明过程．
数学中有些命题的正确性是人们在长期实践中总结出来的，并把它们作为判断其他命题真假的原始依据，这样的真命题叫做公理.
直线公理：两点确定一条直线.
线段公理：两点之间，线段最短.
平行公理：经过直线外的一点有且只有一条直线与已知直线平行.
平行线性质公理：两直线平行，同位角相等.
平行线判定公理：同位角相等，两直线平行.
有些命题是基本事实，还有些命题它们的正确性是经过推理证实的，这样得到的真命题叫做定理.定理也可以作为继续推理的依据.
补角的性质：同角或等角的补角相等.
余角的性质：同角或等角的余角相等.
对顶角相等：对顶角相等.
垂线的性质：①过一点有且只有一条直线与已知直线垂直.
1.在下面的括号内，填上推理的根据.
【选自教材第22页 练习 第1题】
如图，∠A +∠B=180°，求证∠C +∠D=180°.证明：∵∠A+∠B=180°，∴AD∥BC（_________________________），∴∠C+∠D=180°（_________________________）.
同旁内角互补，两直线平行
两直线平行，同旁内角互补
2.如图，在三角形ABC中，点D在边BC的延长线上，CE平分∠ACD，AB∥CE，求证∠A=∠B.
证明：∵CE平分∠ACD (已知)，∴∠ACE=∠DCE(角平分线的定义)．∵AB∥CE(已知)，∴∠A=∠ACE(两直线平行，内错角相等)，∠B=∠DCE(两直线平行，同位角相等)．∴∠A=∠B(等量代换).
3.如图，点D在AB上，直线DG交AF于点E.请从①DG∥AC，②AF平分∠BAC，③∠DAE=∠DEA 中任选两个作为题设，余下一个作为结论，构造一个真命题，并予以证明.题设：_______，结论：_______. (均填写序号)
证明:∵DG∥AC，∴∠DEA=∠EAC．∵AF平分∠BAC，∴∠DAE＝∠EAC.∴∠DAE＝∠DEA．(答案不唯一)
定义：判断一件事情的语句叫做命题
题设：已知事项结论：由已知事项推出的事项
形式：如果……那么……