河南省开封市开封县2022-2023学年八年级上学期期末模拟测试数学试卷(含解析)

这是一份河南省开封市开封县2022-2023学年八年级上学期期末模拟测试数学试卷(含解析)，共15页。试卷主要包含了选择题等内容，欢迎下载使用。

1. 下列图案中，是轴对称图形的是（ ）
A. B. C. D.
2. 冠状病毒是一个大型病毒家族，借助电子显微镜，我们可以看到这些病毒直径约为125纳米（1纳米米），125纳米用科学记数法表示等于（ ）
A. 米B. 米C. 米D. 米
3. 下列运算，正确的是（ ）
A. a3+2a3＝3a6B. （a2）4＝a8
C. a2a3＝a6D. （2ab）2＝2a2b2
4. 现有两根木棒，它们的长是20cm和30cm，若要钉成一个三角形木架，则应选取的第三根木棒长为（ ）
A. 10cmB. 50cmC. 60cmD. 40cm
5. 如图，要测量池塘两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C，D，使BC=CD．再作出BF的垂线DE，使A，C，E三点在一条直线上，通过证明ΔABC≌ΔEDC，得到DE的长就等于AB的长，这里证明三角形全等的依据是（ ）
A. HLB. SASC. SSSD. ASA
6. 下列等式中，不成立的是（ ）
A. B.
C. D.
7. 若一个凸多边形的每一个外角都等于36°，则这个多边形的内角和是（ ）
A. 1080°B. 1260°C. 1440°D. 1620°
8. 如图，在 ABC 中，ED / / BC ，ABC 和 ACB 的平分线分别交 ED 于点 G 、F ，若 FG  2 ，ED  6 ,则EB  DC 的值为（ ）
A. 6B. 7
C. 8D. 9
9. 如图，将长方形ABCD的各边向外作正方形，若四个正方形周长之和为24，面积之和为12，则长方形ABCD的面积为（ ）
A. 4B. C. D. 6
10. 已知关于x的分式方程无解，则k的值为（ ）
A. 0B. 0或-1C. -1D. 0或
二.填空题(共5题，总计 15分)
11. 分解因式：5x4﹣5x2＝________________．
12. 若，则分式__．
13. 一个多边形的每一个内角都是120°，则此多边形从一个顶点出发可以引__________条对角线．
14. 有一三角形纸片ABC，∠A＝70°，点D是AC边上一点，沿BD方向剪开三角形纸片后，发现所得两个纸片均为等腰三角形，则∠C的度数可以是_____．
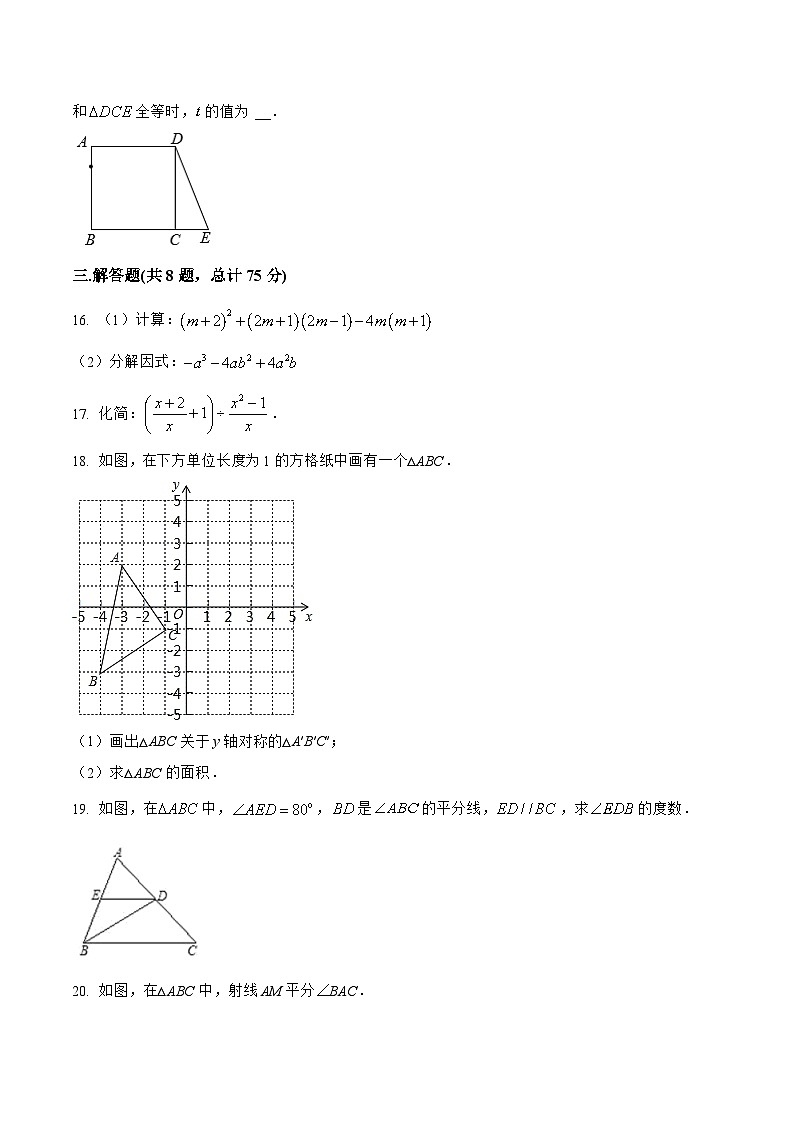
15. 如图，在正方形中，，延长到点，使，连接，动点从点出发，以每秒的速度沿向终点运动．设点的运动时间为秒，当和全等时，的值为 __．
三.解答题(共8题，总计75分)
16. （1）计算：
（2）分解因式：
17. 化简：．
18. 如图，在下方单位长度为1的方格纸中画有一个△ABC．
（1）画出△ABC关于y轴对称△A′B′C′；
（2）求△ABC的面积．
19. 如图，在中，，是的平分线，，求的度数．
20. 如图，在△ABC中，射线AM平分∠BAC．
（1）尺规作图（不写作法，保留作图痕迹）作BC的中垂线，与AM相交于点G，连接BG、CG；
（2）在（1）条件下，∠BAC和∠BGC有何数量关系？并证明你的结论．
21. 实践与探索
如图1，边长为的大正方形有一个边长为的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）
（1）上述操作能验证的等式是__________；（请选择正确的一个）
A． B． C．
（2）请应用这个公式完成下列各题：
①已知，，则__________．
②计算：
22. 刘峰和李明相约周末去科技馆看展览，根据他们的谈话内容，试求李明乘公交车、刘峰骑自行车每小时各行多少千米？
23.
（1）【自主学习】填空：
如图1，点是的平分线上一点，点A在上，用圆规在上截取，连接，可得 ，其理由根据是 ；
（2）【理解运用】如图2，在中，，，平分，试判断和、之间的数量关系并写出证明过程．
（3）【拓展延伸】如图3，在中，，，分别是，的平分线，，交于点，若，，请直接写出的长．
开封县2022-2023学年八年级（上）数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】：C
解析：A选项不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，不符合题意．
B选项不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，不符合题意．
C选项轴对称图形，符合题意．
D选项不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，不符合题意．
2.【答案】：A
解析：解：125纳米=125×10-9米=米，
故选：A．
2.【答案】：B
解析：因为，所以A不符合题意；
因为，所以B符合题意；
因为，所以C不符合题意；
因为，所以D不符合题意．
故选：B．
4.【答案】：D
解析：解：根据三角形三边关系，
∴三角形的第三边x满足：，即，
故选：D．
5.【答案】：D
解析：因为证明在△ABC≌△EDC用到的条件是：CD=BC，∠ABC=∠EDC=90，∠ACB=∠ECD，
所以用到的是两角及这两角的夹边对应相等即ASA这一方法．
故选D
6.【答案】：C
解析：A、，故A不符合题意．
B、，故B不符合题意．
C、，故C符合题意．
D、，故D不符合题意．
故选：C．
7.【答案】：C
解析：该多边形的变数为
此多边形内角和为
故选C
8.【答案】：C
解析：∵ED∥BC，
∴∠EGB=∠GBC，∠DFC=∠FCB，
∵∠GBC=∠GBE，∠FCB=∠FCD，
∴∠EGB=∠EBG，∠DCF=∠DFC，
∴BE=EG，CD=DF，
∵FG=2，ED=6，
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8，
故选C．
9.【答案】：B
解析：解：设AB＝a，AD＝b，由题意得8a＋8b＝24，2a2＋2b2＝12，
即a＋b＝3，a2＋b2＝6，
∴，
即长方形ABCD的面积为，
故选：B．
10.【答案】：D
解析：解：分式方程去分母得： ，即 ，
当，即 时，方程无解；
当x=-1时，-3k+1=-3k，此时k无解；
当x=0时，0=-3k，k=0，方程无解；
综上，k的值为0或 ．
故答案为：D．
二. 填空题
11.【答案】： 5x2（x＋1）（x－1）
解析：5x4-5x2=5x2（x2-1）
=5x2（x+1）（x-1）．
故答案为：5x2（x+1）（x-1）．
12.【答案】：1
解析：原分式，
，
．
故答案为：1．
13.【答案】：3
解析：解：∵一个多边形的每个内角都是120°，
∴这个多边形的每个外角都是60°
∴该多边形的边数为：360°÷60°=6，
∴从这个多边形的一个顶点出发可以画对角线条数为：6﹣3=3．
故答案为：3．
14.【答案】： 20°或35°或27.5°
解析：由题意知△ABD与△DBC均为等腰三角形，
对于△ABD可能有①AB＝BD，此时∠ADB＝∠A＝70°，
∴∠BDC＝180°﹣∠ADB＝180°﹣70°＝110°，
∠C＝（180°﹣110°）＝35°，
②AB＝AD，此时∠ADB＝（180°﹣∠A）＝（180°﹣70°）＝55°，
∴∠BDC＝180°﹣∠ADB＝180°﹣55°＝125°，
∠C＝（180°﹣125°）＝27.5°，
③AD＝BD，此时，∠ADB＝180°﹣2×70°＝40°，
∴∠BDC＝180°﹣∠ADB＝180°﹣40°＝140°，
∠C＝（180°﹣140°）＝20°，
综上所述，∠C度数可以为20°或35°或27.5°．
故答案为：20°或35°或27.5°
15.【答案】： 2或7
解析：∵正方形ABCD,
∴
是直角三角形，
为直角三角形，
点只能在上或者上，
当点在上时，如图，当时，有，
，
，
，
当点在上时，则当时，有，
，
故答案为：2或7．
三.解答题
16【答案】：
（1）
（2）
解析：
【小问1解析】
解：原式；
【小问2解析】
解：原式．
17【答案】：
解析：
解：原式=
=
= ．
18【答案】：
（1）见解析；（2）
解析：
（1）解：关于y轴对称的如下图所示 ：
（2）
．
19【答案】：
40°
解析：
解：∵ED∥BC，∠AED=80°，∴∠ABC=AED=80°；
∵BD是∠ABC的平分线，∴∠DBC∠ABC，∴∠DBC=40°．
∵ED∥BC，∴∠EDB=∠DBC=40°．
20【答案】：
（1）详见解析；（2）∠BAC+∠BGC＝180°，证明详见解析．
解析：
解：（1）线段BC的中垂线EG如图所示：
（2）结论：∠BAC+∠BGC＝180°．
理由：在AB上截取AD＝AC，连接DG．
∵AM平分∠BAC，
∴∠DAG＝∠CAG，
在△DAG和△CAG中
∵
∴△DAG≌△CAG（SAS），
∴∠ADG＝∠ACG，DG＝CG，
∵G在BC的垂直平分线上，
∴BG＝CG，
∴BG＝DG，
∴∠ABG＝∠BDG，
∵∠BDG+∠ADG＝180°，
∴∠ABG+∠ACG＝180°，
∵∠ABG+∠BGC+∠ACG+∠BAC＝360°，
∴∠BAC+∠BGC＝180°．
21【答案】：
（1）A；（2）①4；②5050
解析：
（1）图1表示，图2的面积表示，两个图形阴影面积相等，得到
故选A ；
（2）①
∵
∴，解得
②原式=（1002-992）+（982-972）+…+（42-32）+（22-12）
=（100+99）（100-99）+（98+97）（98-97）+…+（4+3）（4-3）+（2+1）（2-1）
=100+99+98+97+…+4+3+2+1
=101×50
=5050
22【答案】：
刘峰骑自行车每小时行20千米，李明乘公交车每小时行60千米
解析：
解：设刘峰骑自行车每小时行x千米，则李明乘公交车每小时行千米，
根据题意，得，
解得，
经检验，是所列分式方程的解，且符合题意，
∴（千米/时），
答：刘峰骑自行车每小时行20千米，李明乘公交车每小时行60千米．
23【答案】：
（1），SAS
（2），证明见解析
（3）5
解析：
（1）由角平分线的定义得出，根据可证明；
（2）先截取，连接，根据判定，得出，，，进而得出结论；
（3）在上取一点，使，证明，由全等三角形的性质得出，证明，由全等三角形的性质得出，则可求出答案．
【小问1解析】
解：点是的平分线上一点，
，
在和中，
，
，
故答案为：；；
【小问2解析】
．
证明：在上截取，
平分，
，
在和中，
，
，
，AD=DE，
，
，
，
即，
，
，
，
．
【小问3解析】
在上取一点，使，
在中，，
，
，
，
，
，
平分，
，
在和中，
，
，
，
，
，
是的平分线，
，
在和中，
，
，
，
．刘峰：我查好地图了，你看看
李明：好的，我家门口的公交车站，正好有一趟到科技馆那站停的车，我坐明天的车．
刘峰：从地图上看，我家到科技馆的距离比你家近10千米，我就骑自行车去了．
李明：行，根据我的经验，公交车的速度一般是你骑自行车速度的3倍，那你明天早上点从家出发，如顺利，咱俩同时到达．