华东师大版2023-2024学年数学八年级上册期末模拟试卷2(含答案)

这是一份华东师大版2023-2024学年数学八年级上册期末模拟试卷2(含答案)，共14页。试卷主要包含了单选题，填空题，计算题，解答题，综合题等内容，欢迎下载使用。

1．有理数 - 125的立方根为
A．－5 B．5 C．±5 D．－5 5
2．若0＜x＜1，则x，x2， x 的大小关系是（ ）
A．x＜x2＜ xB．x2＜x＜ x C．x ＜x2＜x D．x＜ x ＜x2
3．下列计算正确的是（ ）
A．（﹣a3）2＝a5 B．﹣3a2b+3ba2＝0 C．a2×a3≡a6D．（﹣3a2b）3＝a6b3
4．下列命题是真命题的是（ ）
A．五边形的内角和是720°
B．三角形的重心是这个三角形的三条角平分线的交点
C．内错角相等
D．三角形的任意两边之和大于第三边
5．如图， AD 是 △ABC 的边 BC 上的中线， AB=7，AD=5 ，则 AC 的取值范围为（ ）
A．56．以2022年北京冬奥会为契机，某学校开展以“弘扬奥林匹克精神，感受冰雪运动魅力”为主题的冰雪嘉年华实践课程．为了解学生掌握滑雪技巧及滑雪水平等情况，教练分别对甲、乙两名学生10次训练的结果进行了统计，其中每次训练的成绩分别为5分，4分，3分，2分，1分五档．统计结果如图所示，下列结论正确的是（ ）
A．x甲=x乙，S甲2>S乙2B．x甲=x乙，S甲2C．x甲>x乙，S甲2>S乙2D．x甲7．如图，下面是利用尺规作∠AOB的角平分线OC的作法，在用尺规作角平分线过程中，用到的三角形全等的判定方法是（ ）
作法：
①以O为圆心，适当长为半径画弧，分别交OA，OB于点D，E；
②分别以D，E为圆心，大于 12 DE的长为半径画弧，两弧在∠AOB内交于一点C；
③画射线OC，射线OC就是∠AOB的角平分线．
A．ASAB．SASC．SSSD．AAS
8．如图，在 ΔABC 中， ∠ACB=45°，BC=1，AC=22 ，将 ΔABC 绕点 A 逆时针旋转得到 ΔAB'C' ，其中点 B' 与点 B 是对应点，且点 C，B'，C' 在同一条直线上；则 B'C 的长为（ ）
A．3B．4C．2.5D．32
二、填空题
9．已知一个立方体的体积是27cm3，那么这个立方体的棱长是 cm.
10．若4x2•□=8x3y，则“□”中应填入的代数式是 ．
11．分解因式：2a3﹣8a= ．
12．如图，在△ABC中，AB＝4，AC＝6，∠ABC和∠ACB的平分线交于O点，过点O作BC的平行线交AB于M点，交AC于N点，则△AMN的周长为 ．
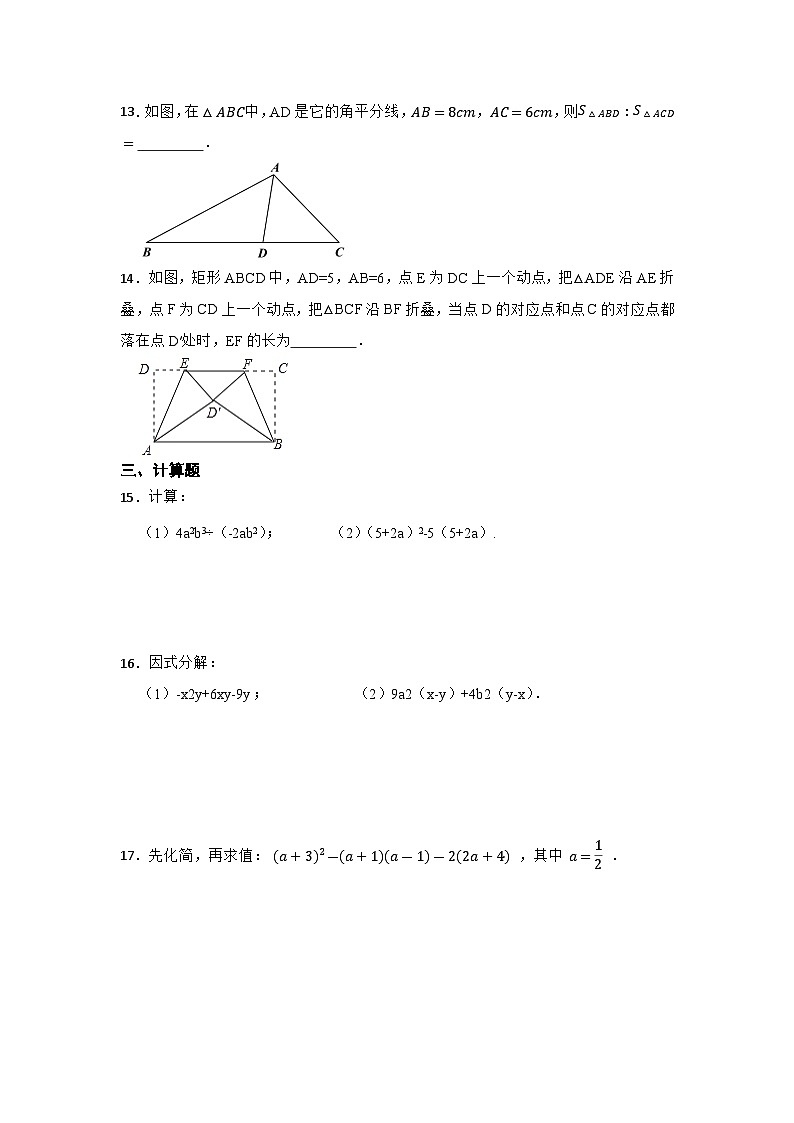
13．如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD= ．
14．如图，矩形ABCD中，AD=5，AB=6，点E为DC上一个动点，把△ADE沿AE折叠，点F为CD上一个动点，把△BCF沿BF折叠，当点D的对应点和点C的对应点都落在点D′处时，EF的长为 ．
三、计算题
15．计算：
（1）4a2b3÷（﹣2ab2）； （2）（5+2a）2﹣5（5+2a）.
16．因式分解：
（1）-x2y+6xy-9y； （2）9a2（x-y）+4b2（y-x）．
17．先化简，再求值： (a+3)2-(a+1)(a-1)-2(2a+4) ，其中 a=12 ．
四、解答题
18．如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE
（1）求证：AD=ED
（2）连接BE，猜想△BEC的形状，并说明理由
19．如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段DE，点A、B、D、E均在小正方形的顶点上．
（1）①在方格纸中画出以AB为一边的锐角等腰三角形ABC，点C在小正方形的顶点上，且 △ABC 的面积为10；
②在方格纸中画出以DE为一边的直角三角形DEF，点F在小正方形的顶点上，且 △DEF 的面积为5；
（2）连接CF，则线段CF长为 ．
20．4月23日是“世界读书日”，某校团委发起了“让阅读成为习惯”的读书活动，鼓励学生利用周末积极阅读课外书籍.为了解该校学生周末两天的读书时间，校团委随机调查了八年级部分学生的读书时间x(单位：分钟)，把读书时间分为四组：A(30≤x<60)，B(60≤x<90)，C(90≤x<120)，D(120≤x<150).部分数据信息如下：
a.B组和C组的所有数据：85 90 60 70 110 75 65 78 100 90 80 95 90
b.根据调查结来绘制了如下尚不完整的统计图：
请根据以上信息，回答下列问题：
（1）被调查的学生共有 ▲ 人，并补全频数分布直方图；
（2）在扇形统计图中，C组所对应的扇形圆心角是 °；
（3）若该校八年级共有400名学生，请估计八年级学生中周末两天读书时间不少于90分钟的人数.
21．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
（1）请判断FC与AD的数量关系，并说明理由；
（2）若AB＝6，AD＝2，求BC的长度．
22．阅读材料：
配方法是初中数学中经常用到的一种重要方法，学好配方法对我们学好数学有很大的帮助，所谓配方就是将某一个多项式变形为一个完全平方式，变形一定要恒等．
例如，解方程x2-4x+4=0，有(x-2)2=0，
∴x=2．
再如，由x2-4x+y2-6y+13=0得：
(x2-4x+4)+(y2-6y+9)=0，
即：(x-2)2+(y-3)2=0，
∴x=2，y=3．
根据上述材料解答下列各题：
（1）若x2-10x+y2+2y+26=0，求xy的值．
（2）若x2-4xy+5y2-2y+1=0，求x+y的值．
（3）若a，b，c表示三角形ABC的三边长，且a2+b2+c2=ab+bc+ca，试说明：三角形ABC是等边三角形．
23．如图1，△ABE是等腰三角形，AB=AE， ∠BAE=45° ，过点B作BC⊥AE于点C，在BC上截取CD=CE，连接AD、DE并延长AD交BE于点P；
（1）求证：AD=BE；
（2）试说明AD⊥BE；
（3）如图2，将△CDE绕着点C旋转一定的角度，那么AD与BE的位置关系是否发生变化，说明理由．
五、综合题
24．如图，在△ABC中，∠C=90°，BC=8，AC=6，AB=10，动点P从点A出发以每秒2个单位长度的速度沿A→C→B运动到点B停止，同时点Q从点B出发，以每秒1个单位长度的速度沿B→C运动，到点C停止，若设点P运动的时间是t秒(t>0)．
（1）点P到达点C时，t= ；到B时，t= 秒；
（2）当CP=BQ时，求t的值；
（3）当点P在边BC上时；
①当△APQ的面积等于12时，直接写出t的值．
②当点P或点Q到边AC和边AB的距离相等时，直接写出t的值．
答案
1．A
2．B
3．B
4．D
5．C
6．A
7．C
8．A
9．3
10． 2xy
11．2a（a+2）（a﹣2）
12．10
13．4∶3
14．83
15．（1）解：4a2b3÷（-2ab2）
=-2ab；
（2）解：（5+2a）2-5（5+2a）
=25+4a2+20a-25-10a
=4a2+10a.
16．（1）解：原式=-yx2-6x+9
=-yx-32
（2）解：原式=x-y9a2-4b2
=x-y3a+2b3a-2b
17．解：原式 =a2+6a+9-(a2-1)-4a-8
=2a+2 ，
∵a=12 ，
∴ 原式 =1+2=3 ．
18．（1）证明：∵∠BAC=90°，点D是BC的中点，
∴AD=BD=CD= 12 BC，
由翻折得DE=BD，
∴AD=DE
（2）解：△BEC是直角三角形．
∵BD=ED
∴∠DBE=∠DEB=x°，
∵CD=ED，
∴∠DCE=∠DEC=y°，
∵2x+2y=180°，
∴x+y=90°
即∠BEC=90°,
所以△BEC是直角三角形.
19．（1）
（2）5
20．解：20；补全频数分布直方图如下：(2)在扇形统计图中，C组所对应的扇形圆心角是______∘；【答案】108(3)若该校八年级共有400名学生，请估计八年级学生中周末两天读书时间不少于90分钟的人数.【答案】解：400×6+320=180（人）答：八年级学生中周末两天读书时间不少于90分钟的有180人.
（1）解：20；补全频数分布直方图如下：
（2）108
（3）解：400×6+320=180（人）
答：八年级学生中周末两天读书时间不少于90分钟的有180人.
21．（1）解：FC=AD，理由如下：
∵AD∥BC（已知），
∴∠ADC=∠ECF（两直线平行，内错角相等），
∵E是CD的中点（已知），
∴DE=EC（中点的定义）．
在△ADE与△FCE中，
∠ADC=∠ECFDE=EC∠AED=∠CEF，
∴△ADE≌△FCE（ASA），
∴FC=AD（全等三角形的性质）；
（2）解：∵△ADE≌△FCE，
∴AE=EF，AD=CF（全等三角形的对应边相等），
∵BE⊥AE，
∴BE是线段AF的垂直平分线，
∴AB=BF=BC+CF，
∴AB=BC+AD，
∵AB=6，AD=2，
∴BC=4．
22．（1）解：x2-10x+y2+2y+26=0
即x2-2·5x+25+y2+2y+1=0，
∴（x-5）2+（y+1）2=0，
∴x=5，y=-1；
则xy=5-1=15.
（2）解：x2-4xy+5y2-2y+1=0
即x2-4xy+4y2+y2-2y+1=0，
∴（x-2y）2+（y-1）2=0，
∴x-2y=0，y=1，
∴x=2，
则x+y=2+1=3
（3）解：△ABC为等边三角形．理由如下：
∵a2+b2+c2=ac+ab+bc，
即a2+b2+c2-ac-ab-bc=0，
∴2a2+2b2+2c2-2ac-2ab-2bc=0，
即a2+b2-2ab+b2+c2-2bc+a2+c2-2ac=0，
∴（a-b）2+（b-c）2+（c-a）2=0，
∴a-b=0，b-c=0，c-a=0，
∴a=b=c，
∴△ABC为等边三角形.
23．（1）证明：∵BC⊥AE，∠BAE=45°，
∴∠CBA=∠CAB，
∴BC=CA，
在△BCE和△ACD中， BC=AC∠BCE=∠ACD=90°CE=CD ，
∴△BCE≌△ACD(SAS)，
∴AD=BE；
（2）解：∵△BCE≌△ACD，
∴∠CBE=∠CAD，
∵∠CAD+∠ADC=90°，∠BDP=∠ADC，
∴∠CBE+∠BDP=90°，
∴∠APB=90°，
∴AD⊥BE；
（3）解：AD与BE的位置关系不发生改变．
如图2，
∵∠BCA=∠ECD=90° ，
∴∠BCA+∠BCD=∠ECD+∠BCD ，
∴∠BCE＝∠ACD，
在△BCE和△ACD中， BC=AC∠BCE=∠ACDCE=CD ，
∵△BCE≌△ACD(SAS)，
∴BE=AD，∠EBC=∠DAC，
∵∠BFP=∠AFC，
∴∠BPF=∠ACF=90°，
∴AD⊥BE．
24．（1）3；7
（2）解： 当点P在线段AC上时，AP=2t，则PC=6-2t，
∴6-2t=t，
∴t=2．
当点P在线段CB上时，PC=2t-6，
∴2t-6=t，
∴t=6，
综上，当t=2或6时，CP＝BQ。
（3）①t=6或103
②t=4.5或5