专题05 轴对称重难点题型分类-2022-2023学年八年级数学上册重难点题型期末复习热点题型（人教版）

这是一份专题05 轴对称重难点题型分类-2022-2023学年八年级数学上册重难点题型期末复习热点题型（人教版），文件包含专题05轴对称重难点题型分类原卷版2022-2023学年八年级数学上册重难点题型分类高分必刷题人教版docx、专题05轴对称重难点题型分类解析版2022-2023学年八年级数学上册重难点题型分类高分必刷题人教版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

期末试题中的典型考题，具体包含的题型有：轴对称图形、垂直平分线的性质与判定、尺规作图、最短路径问题、等腰三角形的性质与判定、等边三角形的性质与判定。适合于培训机构的老师给学生作培训时使用或者学生考前刷题时使用。
题型一 轴对称图形
1．（2021·湖南）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．B．C．D．
2．（2021·辽宁）若点M(2，a)和点N(a+b，3)关于y轴对称，则a、b的值为（ ）
A．a=3，b=－5B．a=－3，b=5C．a=3，b=5D．a=－3，b=1
3.如图，是小亮在镜中看到身后墙上的时钟，此时时钟的实际时刻是（ ）
A．3：55B．8：05C．3：05D．8：55
4．（2022·浙江）如图，把一张长方形纸片沿折叠后与的交点为，、分别在、的位置上，若，则的值为（ ）
A．B．C．D．
题型二 垂直平分线的性质与判定
1. 垂直平分线的定义
经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）．
2. 垂直平分线的性质
垂直平分线上任意一点,到线段两端点的距离相等.．
3.垂直平分线的判定
到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
5．（2015·湖北）如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）
A．8B．9C．10D．11
6.（2017·湖北）如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为( )
A．30°B．45°C．50°D．75°
7．如图，∠BAC＝110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（ ）
A．20°B．40°C．50°D．60°
8．（2021·宁夏）如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．
（1）求∠ECD的度数；（2）若CE＝5，求BC长．
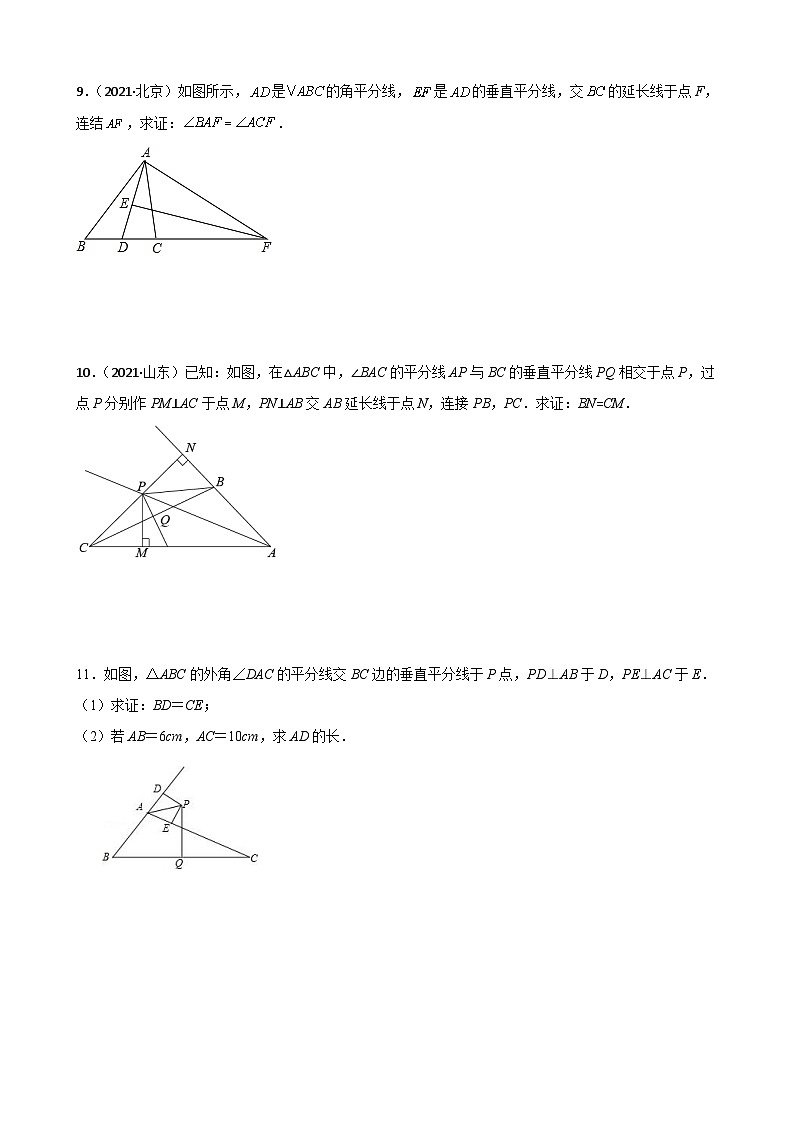
9．（2021·北京）如图所示，是的角平分线，是的垂直平分线，交的延长线于点F，连结，求证：．
10．（2021·山东）已知：如图，在△ABC中，∠BAC的平分线AP与BC的垂直平分线PQ相交于点P，过点P分别作PM⊥AC于点M，PN⊥AB交AB延长线于点N，连接PB，PC．求证：BN=CM．
11．如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点，PD⊥AB于D，PE⊥AC于E．
（1）求证：BD＝CE；
（2）若AB＝6cm，AC＝10cm，求AD的长．
12．已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线D交于点D，DM⊥AB于M，DN⊥AC的延长线于N．
（1）证明：BM＝CN；
（2）当∠BAC＝70°时，求∠DCB的度数．
13．（2022·广东）如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E，
（1）若∠BAC=50°，求∠EDA的度数；
（2）求证：直线AD是线段CE的垂直平分线．
14．（2019·广东）如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．
求证：（1）∠ECD=∠EDC；
（2）OC=OD；
（3）OE是线段CD的垂直平分线．
题型三 尺规作图
15．（2022·辽宁）已知在中，点为线段边上一点，则按照顺序，线段分别是的（ ）
A．①中线，②角平分线，③高线B．①高线，②中线，③角平分线
C．①角平分线，②高线，③中线D．①高线，②角平分线，③中线
16．（2022·山东）如图，在中，分别以点和点为圆心，大于的长为半径画弧，两弧相交于点，，作直线，交于点，连接．若的周长为12，，则的周长为（ ）
A．10B．9C．8D．7
17．（2022·福建）如图，已知△ABC．
(1)求作BC边上高AD，交BC于点D，∠BAC的平分线AE，交BC于点E（要求：尺规作图，不写作法，保留作图痕迹）．
(2)若∠B＝35°，∠C＝65°，求∠DAE的度数．
18．按要求完成下列作图，不要求写作法，只保留作图痕迹．
（1）已知：线段AB，作出线段AB的垂直平分线MN．
（2）已知：∠AOB，作出∠AOB的平分线OC．
19．（2020·北京）如图，已知∠BAC及两点M、N．
求作：点P，使得PM＝PN，且P到∠BAC两边的距离相等．

题型四 最短路径问题
20.（青竹湖）如图，在△中，，、 是△的两条中线，是上一个动点，则下列线段的长度等于最小值的是（ ）

21．已知∠MON＝40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数是（ ）
A．40°B．100°C．140°D．50°
22．（2020·北京）如图，在平面直角坐标系xOy中，点O(0，0)，A(－1，2)，B(2，1)．
在图中画出△AOB关于y轴对称的△A1OB1，并直接写出点A1和点B1的坐标；
(2)在x轴上画出点P，使得PA+PB的值最小．
23．（北雅）阅读下列一段文字：已知在平面内两点P1（x1，y1）、P2（x2、y2），其两点间的距离P1P2＝问题解决：已知A（1，5），B（7，3）
（1）试求A、B两点的距离；
（2）在x轴上找一点P（不求坐标，画出图形即可），使PA+PB的长度最短，求出PA+PB的最短长度．
（3）在x轴上有一点M，在y轴上有一点N，连接A、N、M、B得四边形ANMB，若四边形ANMB的周长最短，请找到点M、N（不求坐标，画出图形即可），求出四边形ANMB的最小周长．
题型五 等腰三角形的性质与判定
1.定义：两条边相等的三角形是等腰三角形。
2.等腰三角形的性质定理及推论：
定理：等腰三角形的两个底角相等（简称：等边对等角）
推论1：等腰三角形顶角平分线平分底边并且垂直于底边。即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。（简称：三线合一）
24．已知等腰三角形的两边长分别是4和6，则它的周长是（ ）
A．14B．16C．18D．14或16
25．（2022·四川）如图，已知中，，，和的平分线相交于点，过点作的平行线，分别交，于，，则的周长是__________．
26．（2020·北京）等腰△ABC的一个角为30°，则其顶角度数为__________．
27．（2021·广西）如图，在△ABE中，∠A＝105°，AE的垂直平分线MN交BE于点C，且AB+BC＝BE，则∠B的度数是（ ）
A．45°B．60°C．50°D．55°
28．（2022·贵州）如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）
A．30°B．40°C．36°D．70°
29.若等腰三角形一腰上的高与另一腰的夹角为40°，则这个等腰三角形的底角度数是 ．
30．（2022·江苏）已知：如图△ABC中，AB=AC，AD和BE是高，它们交于点H，且AE=BE．求证：
(1)△AHE≌△BCE；
(2)AH=2BD．
31．（2020·北京）已知：在△ABC中，∠ABC=45°，于点D，点E为CD上一点，且DE=AD，连接BE并延长交AC于点F，连接DF．求证：BE=AC．
32．（2021·重庆）在中，，，点为的中点，、分别在、上，且．
(1)求证：；
(2)判断的形状，并说明理由．
33．（2021·河北）如图，△ABC和△AOD是等腰直角三角形，AB=AC，AO=AD，∠BAC=∠OAD=90°，点O是△ABC内的一点，∠BOC=130°．
（1）求证：OB=DC；
（2）求∠DCO的大小；
（3）设∠AOB=α，那么当α为多少度时，△COD是等腰三角形．
34．如图，点C在线段AB上，AD∥EB，AC＝BE，AD＝BC，DE与BC交于点G，CF平分∠DCE．
（1）求证：△CDE为等腰三角形；
（2）试判断CF、DE的位置关系，并说明理由．
题型六 等边三角形的性质与判定
1、等边三角形的性质：三边相等；三个角都等于60∘；30∘角所对的直角边是斜边的一半。
2、等边三角形的判定：三条边相等；两个角等于60∘；两边相等 + 一个60∘的角。
35．（2021·山东）如图，已知直线，将等边三角形如图放置．若，则等于（ ）
A．17°B．22°C．27°D．32°
36．（2021·四川）如图，点D、E分别在等边三角形ABC的边BC、AC上，且BD=CE，连接AD、BE相交于点P，则∠APE的度数是（ ）
A．60°B．55°C．45°D．30°
37．（2021·福建）下列说法错误的是（ ）
A．角是轴对称图形，角平分线所在的直线是它的对称轴
B．等腰三角形一边上的中线和这条边上的高重合
C．三角形三条边上的中垂线的交点到三个顶点的距离相等
D．有两个角是60°的三角形是等边三角形
38．下面给出几种三角形：（1）有两个角为60°的三角形；（2）三个外角都相等的三角形；（3）一边上的高也是这边上的中线的三角形；（4）有一个角为60°的等腰三角形，其中是等边三角形的个数是（ ）
A．4个B．3个C．2个D．1个
39．（2021·四川）如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=1，则EF=___．
40．（2021·重庆）如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，AD恰好平分∠BAC，若DE＝1，则BC的长是_____．
41．如图，在△ABC中，AB＝AC，∠BAC＝120°，D为BC中点，DE⊥AB于E，AD＝4，求线段BE的长度．
42．（2021·云南）如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
（1）求∠F的度数；
（2）若CD=2，求DF的长．
43．如图，点P，M，N分别在等边△ABC的各边上，且MP⊥AB于点P，MN⊥BC于点M，PN⊥AC于点N．
（1）求证：△PMN是等边三角形；
（2）若AB＝18cm，求CM的长．
44．如图，△ABC是等边三角形，BD⊥AC，AE⊥BC，垂足分别为D、E，AE、BD相交于点O，连接DE．
（1）判断△CDE的形状，并说明理由．
（2）若AO＝12，求OE的长．
45．已知，如图，△ABC为等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1．
（1）求证：△ABE≌△CAD；
（2）求∠BPQ的度数；
（3）求AD的长．
46．（2019·重庆）如图，P为等边△ABC外一点，AH垂直平分PC于点H，∠BAP的平分线交PC于点D．
（1）求证：DP＝DB；
（2）求证：DA+DB＝DC；
A.
B.
C.
D.