考点巩固卷12 平面向量（十二大考点）-备战2024年高考数学一轮复习高分突破（新高考通用）

这是一份考点巩固卷12 平面向量（十二大考点）-备战2024年高考数学一轮复习高分突破（新高考通用），文件包含考点巩固卷12平面向量十二大考点原卷版docx、考点巩固卷12平面向量十二大考点解析版docx等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。

考点01平面向量的基本概念
1．下列说法错误的是（ ）
A．向量与的长度相等B．两个相等向量若起点相同，则终点相同
C．共线的单位向量都相等D．只有零向量的模等于0
【答案】C
【分析】根据相反向量、相等向量、单位向量和零向量的定义判断各个选项．
【详解】对于A，向量与互为相反向量，其长度相等，故A正确；
对于B，因为相等向量的方向相同，长度相等，则两个相等的向量，若起点相同，则终点也相同，故B正确；
对于C，共线的单位向量可以是相反向量，故C错误；
对于D，因为模长为0的向量为零向量，所以只有零向量的模长等于0，故D正确．
故选：C．
2．给出下列3个命题，①相等向量是共线向量；（2）若与不相等，则向量与是不共线向量；③平行于同一个向量的两个向量是共线向量；其中真命题的个数是（ ）
A．0B．1C．2D．3
【答案】B
【分析】根据相等向量、共线向量的定义判断即可.
【详解】长度相等且方向相同的向量叫做相等向量，故相等向量一定是共线向量，即①正确；
若与不相等，则向量与也可以共线，只要与模不同即可，故②错误；
平行于同一个向量的两个向量不一定是共线向量，如，，，
此时，，但是与不一定共线，故③错误；即真命题只有个.
故选：B
3．（多选）下列叙述中正确的是（ ）
A．若，则
B．若，则
C．已知非零向量与且//，则与的方向相同或相反
D．对任一非零向量是一个单位向量
【答案】CD
【分析】A注意即可判断；B根据向量的性质判断；C由共线向量的定义判断；D由单位向量的定义判断.
【详解】A：若时，不一定有，错误；
B：向量不能比较大小，错误；
C：非零向量与且//，则与的方向相同或相反，正确；
D：非零向量，则是一个单位向量，正确.
故选：CD
4．（多选）下列说法正确的有（ ）
A．
B．λ、μ为非零实数，若，则与共线
C．两个向量不能比较大小，但它们的模能比较大小
D．若平面内有四个点A、B、C、D，则必有
【答案】BCD
【分析】利用向量数量积的定义可判断A；利用向量共线定理可判断B；根据向量的概念可判断C；利用向量的减法运算可判断D.
【详解】对于A选项，，故错误；
对于B选项，因为为非零实数，且，与一定共线，故正确；
对于C选项，向量不能比较大小；向量的模可比较大小，故正确；
对于D选项，由，所以，故正确.
故选：BCD.
5．（多选）下列关于平面向量的说法中不正确的是（ ）
A．已知非零向量，，，若，，则
B．若，则为平行四边形
C．若且，则
D．若点G为的重心，则
【答案】BC
【分析】根据向量共线的概念可判断选项A,B；利用向量垂直的数量积关系即可判断C错误；利用三角形重心的结论即可判断选项D.
【详解】对于选项A，对于非零向量，，，由，，且为非零向量，可知，选项A正确；
对于选项B，因为，则四点可能共线，所以不一定为平行四边形，故选项B错误；
对于选项C，由可得，则，不一定，故选项C错误；
对于选项D，由平面向量中三角形重心的结论可知，若点G为的重心，则，故选项D正确，
故选项：BC.
考点02平面向量的线性运算
6．如图，向量，，，则向量（ ）

A．B．C．D．
【答案】C
【分析】根据向量的加减法求解即可.
【详解】依题意，得，
故选：C．
7．在正六边形中，（ ）
A．B．C．D．
【答案】C
【分析】根据平面向量运算求得正确答案.
【详解】依题意，.
故选：C

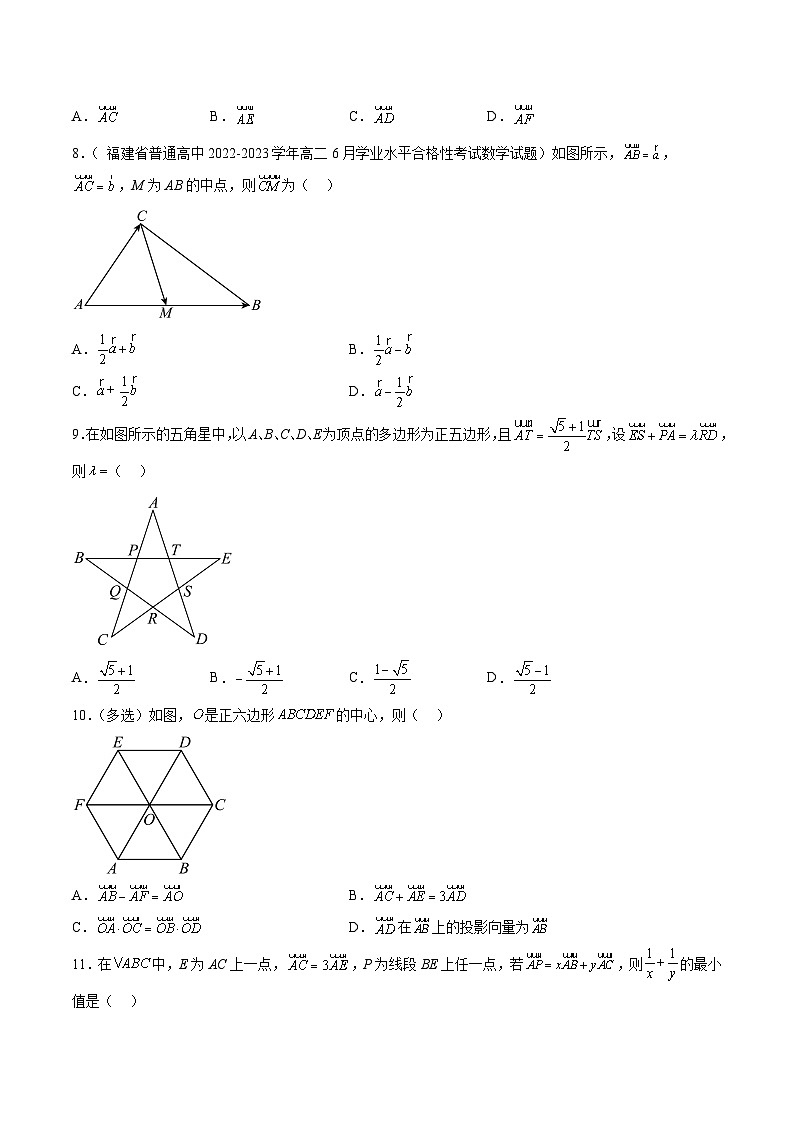
8．（ 福建省普通高中2022-2023学年高二6月学业水平合格性考试数学试题）如图所示，，，M为AB的中点，则为（ ）

A．B．
C．D．
【答案】B
【分析】根据给定条件，利用向量的加法列式作答.
【详解】，，M为AB的中点，
所以.
故选：B
9．在如图所示的五角星中，以A、B、C、D、E为顶点的多边形为正五边形，且，设，则（ ）

A．B．C．D．
【答案】C
【分析】将转化为，结合已知可得.
【详解】在五角星中，，，则，
，
，
，
.
故选：C.
10．（多选）如图，是正六边形的中心，则（ ）

A．B．
C．D．在上的投影向量为
【答案】CD
【分析】根据向量的线性运算法则，可判定A、B不正确，结合向量的数量积的定义域运算，可判定C正确，结合向量的投影的定义与运算，可判定D正确.
【详解】根据题意，结合平面向量的线性运算法则，可得：
对于A中，由，所以A不正确；
对于B中，由，所以B不正确；
对于C中，设正六边形的边长为，可得，，所以，所以C正确；
对于D中，如图所示，连接，可得，
可得，所以在向量上的投影向量为，所以D正确.
故选：CD.

11．在中，E为AC上一点，，P为线段BE上任一点，若，则的最小值是（ ）
A．B．C．6D．8
【答案】B
【分析】由题可得，后由基本不等式可得答案.
【详解】由题可得B，P，E三点共线，则.
又，，则，则.
当且仅当，即时取等号.
故选：B

考点03向量共线与三点共线
12．设，是两个不共线的向量，关于向量，有①，；②，；③；，④；．其中，共线的有________．（填序号）
【答案】①②③
【分析】根据向量共线的条件对各选项逐一判断即可.
【详解】①，共线；
②，共线；
③，共线；
④和无法表示成，所以不共线.
故答案为：①②③
13．如图，在中，是的中点，是线段上靠近点的三等分点，设.

(1)用向量与表示向量；
(2)若，求证：三点共线.
【答案】(1)，
(2)证明见解析
【分析】（1）利用向量的线性运算及平面向量的基本定理即可求解；
（2）利用向量的线性运算及向量共线的充要条件即可求解.
【详解】（1）是的中点，
；
.
（2），
与平行，
又与有公共点，
三点共线.
14．设是不共线的两个向量，.若三点共线，则k的值为__________.
【答案】
【分析】根据三点共线可得向量共线，由此利用向量共线定理可列出向量等式，即可求得答案.
【详解】因为三点共线，故,
则，使得，
又，
故，则，解得，
故答案为：
15．在中，，且，则________．
【答案】
【分析】根据平面向量的线性运算求解即可.
【详解】，，
即，，．
故答案为：.
16．已知，是平面上的非零向量，则“存在实数，使得”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【分析】根据充分性必要性的定义，结合向量共线的结论进行判断.
【详解】因为分别表示与方向相同的单位向量，所以由可知，方向相同；
“存在实数，使得”即共线，包含方向相同或方向相反两种情况．
所以，“存在实数，使得”不能推出是“”；
“” 可以推出“存在实数，使得”，
所以“存在实数，使得”是“”的必要不充分条件．
故选：B.
17．已知是不共线的向量，且，则（ ）
A．A、B、D三点共线B．A、B、C三点共线
C．B、C、D三点共线D．A、C、D三点共线
【答案】D
【分析】利用平面向量共线向量定理求解.
【详解】因为，
所以，
若A、B、D三点共线，则，而 无解，故A错误；
因为，
所以，
若A、B、C三点共线，则，而 无解，故B错误；
因为，
所以，
若B、C、D三点共线，则，而 无解，故C错误；
因为，
所以，
即，所以A、C、D三点共线，故D正确.
故选：D
考点04平面向量共线定理的推论
18．如图所示，在中，，P是上的一点，若，则实数m的值为（ ）．

A．B．C．D．
【答案】D
【分析】利用共线定理的推论可得.
【详解】因为，所以，
所以，
因为P，B，N三点共线，所以，解得.
故选：D
19．如图，在△ABC中，点P在边BC上，且，过点P的直线l与射线AB，AC分别交于不同的两点M，N，若，，则实数的值是（ ）

A．B．C．D．
【答案】B
【分析】结合向量的运算可得，然后由三点共线得，可得答案.
【详解】由题意知：，
又，，即，
由三点共线，可得，即.
故选：B.
20．已知长方形中，，是线段的中点，是线段上靠近的三等分点，线段，交于点，则（ ）
A．B．
C．D．
【答案】A
【分析】设，根据平面向量线性运算及平面共线定理的推论以，结合平面向量基本定理，即可求得的值，从而得结论.
【详解】由题可知，

设
则
,
又
，
所以，解得，所以.
故选：A.
21．在中，点O满足，过点O的直线分别交射线AB，AC于点M，N，且，，则的最小值为（ ）
A．B．C．3D．4
【答案】A
【分析】利用共线定理的推论可得，然后妙用“1”可得.
【详解】由题可知，，
因为，，所以，，
又，所以，
所以，
因为三点共线，所以，
所以，
当且仅当，即时，等号成立.
所以的最小值为.
故选：A

22．已知A，B，P是直线l上不同的三点，点O在直线l外，若，则（ ）
A．2B．C．3D．
【答案】A
【分析】根据已知等式，结合向量减法法则化简，而三点共线，可得，解得的值，设，可得，所以，从而求出的值．
【详解】，，
整理得，，
当时，显然不成立，故，
所以，
，，是直线上不同的三点，
，解得，，
设，，
，
，解得，即．
故选：A．
23．在中，点是边所在直线上的一点，且，点在直线上，若向量，则的最小值为（ ）
A．3B．4C．D．9
【答案】B
【分析】由题意可得，又点，，三点共线，所以，再利用“1”的代换，结合基本不等式求解即可．
【详解】，，
，
点，，三点共线，
，
又，，
，
当且仅当，即，时，等号成立，
的最小值为4．
故选：B．
考点05平面向量基本定理
24．（多选）已知M为△ABC的重心，D为边BC的中点，则（ ）
A．B．
C．D．
【答案】ABC
【分析】根据三角形重心的性质及向量的线性运算、基本定理一一判定即可.
【详解】如图，根据向量加法的平行四边形法则，易得，故A正确；
由题意得M为线段AD的靠近D点的三等分点，所以，
又，所以，故B正确；
，故C正确；
，，又，所以，故D错误.

故选：ABC
25．如图，在的方格中，已知向量的起点和终点均在格点，且满足，那么______.

【答案】1
【分析】可作单位向量，从而可用表示向量，根据平面向量基本定理即可得出关于的方程组，求解即可.
【详解】如图所示，作单位向量,

则，，
所以.
又，所以,
所以，解得，
所以.
故答案为:1.
26．在中，点为与的交点，，则（ ）
A．0B．C．D．
【答案】B
【分析】利用平面向量基本定理得到，，从而列出方程组，求出，得到，求出答案.
【详解】因为，所以为中点，
三点共线，故可设，即，
整理得，
因为，所以，即，
三点共线，
可得，
所以，解得，
可得，则，.
故选：B
27．如果表示平面内所有向量的一个基底，那么下列四组向量，不能作为一个基底的是（ ）
A．、B．、
C．、D．、
【答案】C
【分析】利用平面向量基底的定义逐项判断，可得出合适的选项.
【详解】对于A选项，设，
因为、不共线，则，显然不成立，A中的两个向量可作一个基底；
对于B选项，设，
因为、不共线，则，显然不成立，B中的两个向量可作一个基底；
对于C选项，因为，C中的两个向量不能作一个基底；
对于D选项，设，
因为、不共线，则，显然不成立，D中的两个向量可作一个基底.
故选：C.
28．如图，在梯形ABCD中，，E，F分别是AB，BC的中点，AC与DE相交于点O，设，．

(1)用，表示；
(2)用，表示．
【答案】(1)
(2)
【分析】（1）由题设知且，根据用表示出即可；
（2）由题意可得，再用表示出即可.
【详解】（1）在中，因为E，F分别是AB，BC的中点，所以，且，
故.
（2）因为，所以，则，
故
.
29．如图，在中，点，分别在边和边上，，分别为和的三等分点，点靠近点，点靠近点，交于点，设，，则（ ）

A．B．
C．D．
【答案】B
【分析】利用表示，结合平面向量基本定理确定其表达式.
【详解】设，，
所以，
又，
所以，
因为，
所以，
所以，解得，
所以，
故选：B.
考点06平面向量的坐标运算
30．已知向量，且，则（ ）
A．B．C．D．
【答案】C
【分析】根据平面向量共线的坐标公式计算即可.
【详解】因为，且，
所以，所以.
故选：C.
31．若，，C为AB的中点，D为AB上更靠近A的三等分点，则C的坐标为______，D的坐标为______．
【答案】
【分析】根据中点的坐标公式求的坐标，利用求的坐标.
【详解】根据中点坐标公式，的坐标为，
，则．因为，所以的坐标为．
故答案为：，
32．在平面直角坐标系xOy中，，，．
(1)若，求实数x，y的值；
(2)若，求实数m的值．
【答案】(1)
(2)
【分析】（1）利用向量坐标化的线性运算即可得到关于的方程组，解出即可；
（2）首先计算得，再利用向量共线得到关于的方程，解出即可.
【详解】（1）由，有，
有解得
故；
（2）由，，
又由，有，
解得，故．
33．已知边长为1的正方形ABCD中，AB与x轴正半轴成30°角．求点B和点D的坐标和与的坐标及点C的坐标．

【答案】，，，．
【分析】根据题意，得，．由此结合三角函数的定义，算出点、两点的坐标，进而可得到与的坐标．由向量相等即可求解.
【详解】由题意，点在原点，与轴正半轴成,
可得，．
设，，，．
则，，，．
同理可得，，，．
，，，．
由于
34．已知，，．
(1)若，求的值；
(2)若，且，，三点共线，求的值．
【答案】(1)
(2)
【分析】（1）首先求出的坐标，再根据向量共线的坐标表示得到方程，解得即可；
（2）首先求出，的坐标，依题意，根据向量共线的坐标表示得到方程，解得即可；
【详解】（1）因为，，所以，
因为，所以，解得.
（2）因为，，
因为，，三点共线，所以，所以，解得，
故的值为．
35．在矩形中，，，E为CD的中点，若，，则________．
【答案】
【分析】建立如下图的平面直角坐标系，求出各点坐标，由平面向量线性运算的坐标表示可得的坐标，由，列方程组，解方程组可得和的值即可求解.
【详解】建立如下图的平面直角坐标系，
由已知得，，，，
由得，
设，则，
可得，解得，所以，，
又因为，
所以，解得，，则.
故答案为：.
考点07求数量积
36．在平面直角坐标系中，设向量，
(1)当时，求，的值；
(2)若且，求的值.
【答案】(1)，
(2)
【分析】（1）根据特殊角的三角函数值代入计算可得；
（2）根据数量积的坐标表示，利用二倍角公式、辅助角公式将式子化简，即可得到，从而求出，即可得解.
【详解】（1）因为，
当时，，
所以，，
（2）∵，，
∴
，
∴，
∵，，∴，解得，
∴.
37．已知，，.
(1)若，求；
(2)设，求的单调递增区间.
【答案】(1)
(2)，.
【分析】（1）当时，写出向量、的坐标，利用平面向量数量积的坐标运算可求得的值；
（2）利用平面向量数量积的坐标运算以及辅助角公式化简函数的解析式，利用正弦型函数的单调性可求得函数的单调递增区间.
【详解】（1）解：当时，则，，所以，.
（2）解：因为，
由，，
解得，.
所以的单调递增区间为，.
38．已知，，且与夹角为求：
(1)
(2)
【答案】(1)
(2)
【分析】（1）由平面向量的数量积的定义求解即可；
（2）由平面向量的数量积的运算律求解即可.
【详解】（1）因为，，且与夹角为，
所以.
（2）.
39．如图，设、是平面内相交成角的两条数轴，、分别是与轴、轴正方向同向的单位向量，若向量，则把有序数对叫做向量在坐标系中的坐标.若在该坐标系中，，，则______.

【答案】
【分析】利用平面向量数量积的定义可求得的值，由题意得出，，利用平面向量数量积的运算性质可求得的值.
【详解】由平面向量数量积的定义可得，
由题意可得，，
所以，.
故答案为：.
40．已知四边形是矩形，，，则（ ）
A．B．-7C．D．-25
【答案】B
【详解】利用平面向量数量积的运算律计算求值即可．
【分析】
.
故选：B
41．如图所示，正方形的边长为2，为的中点，为的中点，则（ ）

A．B．
C．D．
【答案】D
【分析】先将用表示，再根据数量积的运算律即可得解.
【详解】由题意，，
所以.
故选：D.
考点08垂直关系的判断及应用
42．已知平面向量，，向量与的夹角为．
(1)求与；
(2)求证：．
【答案】(1)；
(2)证明见解析
【分析】（1）代入向量数量积，以及模的计算公式，即可求解；
（2）要证明向量垂直，转化为证明.
【详解】（1）由题意，，
；
（2）证明：由（1）得，
所以，
故．
43．已知平面向量，，，，，则的值是______.
【答案】
【分析】先利用向量垂直数量积为0求出的值，再根据向量的平方等于模长的平方即可求解.
【详解】，
因为，所以，解得，
又因为，
所以，
故答案为：
44．已知向量，．
(1)若，求；
(2)若，求实数的值．
【答案】(1)
(2)
【分析】（1）由数量积坐标表示求解即可；
（2）计算，由垂直向量的坐标表示求解即可.
【详解】（1）时，，，
所以．
（2），
，
因为，
所以
整理得，故．
45．已知向量.
(1)若点A，B，C不能构成三角形，求实数应满足的条件；
(2)若为直角三角形，求实数的值.
【答案】(1)
(2)或
【分析】（1）当三点共线时，点A，B，C不能构成三角形，即共线，利用向量共线的坐标公式计算即可得出答案.
（2）为直角三角形，分为直角，为直角和为直角，利用垂直向量的坐标表示即可得出答案.
【详解】（1）因为点A，B，C不能构成三角形，所以，
因为，，，
所以，
，
，所以，解得，
综上可得，当时，A，B，C不能构成三角形；
（2）①若为直角，则，所以，
解得；
②若为直角，则，
所以，解得；
③若为直角，则，
所以，
即，因为，所以方程无解；
综上可得，当或时为直角三角形.
46．已知，，与的夹角是，求：
(1)
(2)当为何值时，
【答案】(1)
(2)
【分析】（1）根据向量数量积定义和运算律可求得，从而得到；
（2）利用向量垂直与数量积的运算律得到关于的方程，从而得解.
【详解】（1）因为，，与的夹角是，
所以，
故，
则.
（2）因为，所以，
则，即，
所以.
47．已知向量 ， ，若 ，则的值为（ ）
A．B．C．D．
【答案】A
【分析】利用平面向量垂直的坐标表示求出的值，利用二倍角公式以及弦化切可求得所求代数式的值.
【详解】已知向量 ， ，且，
则，即，
若，则，这与矛盾，
所以，，故，
因此，
.
故选：A.
考点09向量的模
48．已知向量与满足，，与的夹角为.
(1)求；
(2)求；
(3)当为何值时，？
【答案】(1)；
(2)；
(3).
【分析】（1）利用数量积的定义直接计算作答.
（2）利用数量积的运算律，结合（1）的结论求解作答.
（3）利用垂直关系的向量表示不解作答.
【详解】（1）因为，，与的夹角为，所以.
（2）由（1）知，所以.
（3）由，得，解得，
所以当时，.
49．已知三个不共线的平面向量，，两两所成的角相等，，，，则______.
【答案】5
【分析】由平面向量两两所成角相等可得两两所成角为，再利用数量积运算性质即可得出.
【详解】由题知三个不共线的平面向量两两夹角相等，可得任意两向量的夹角是，
因为，，，
所以
，
所以.
故答案为：5
50．如图，四边形ABCD为筝形（有一条对角线所在直线为对称轴的四边形），满足，AD的中点为E，，则筝形ABCD的面积取到最大值时，AB边长为___________.

【答案】
【分析】建立坐标系，利用向量法结合基本不等式得出，进而得出AB边长.
【详解】以点为坐标原点，建立如下图所示的直角坐标系.
设，
则.
因为，所以，
即，当且仅当时，取等号.
筝形ABCD的面积为
即当时，筝形ABCD的面积最大.
此时AB边长为.
故答案为：

51．如图，在平面四边形中，，，，则的最小值为__________．

【答案】
【分析】建立如图所示的平面直角坐标系，设，利用垂直关系和模的坐标公式可得，故可求模的最小值.
【详解】以为原点建立如图所示的平面直角坐标系，设，

因为，且，故，
故，，
故，
而，故，故，
即，
所以
，
当时，.
故答案为：
52．（ 2023·河南驻马店·统考三模）已知平面向量满足,且，则=_________________ ．
【答案】
【分析】由数量积的运算律求出，再由向量的模长公式即可得出答案.
【详解】由,得,
所以.
故答案为：
53．已知两点，，且在线段AB上，若，则点的坐标为（ ）
A．B．
C．D．
【答案】C
【分析】设点，表示出，由条件可得，再利用在线段AB上可得，联立即可求得答案.
【详解】设点，则，
由得，
即①，
又在线段AB上，故共线，
则②，
①②联立得，而在线段AB上，则，
故，解得，（舍去），
则，故,
故选：C
考点10求两个向量的夹角
54．已知为坐标原点，点，则__________.
【答案】
【分析】利用向量的坐标运算得到点坐标，然后利用数量积求夹角即可.
【详解】设点，所以，，，，
因为，所以，解得，，
因为，所以.
故答案为：.
55．向量与的夹角为（ ）
A．B．C．D．
【答案】A
【分析】根据向量的坐标运算求解.
【详解】因为，
则，且，
所以.
故选：A.
56．设两个向量，满足，．
(1)若，求，的夹角；
(2)若，的夹角为60°，向量与的夹角为锐角，求实数的取值范围．
【答案】(1)
(2)且.
【分析】（1）根据数量积运算以及结果，结合模长，即可求得，再根据数量积求得夹角；
（2）根据夹角为锐角则数量积为正数，求得的范围，再排除向量与不为同向共线向量对应参数的范围，则问题得解.
【详解】（1）因为，所以，
又，，所以，
所以，又，
所以向量、的夹角是.
（2）因为向量与的夹角为锐角，所以，
且向量与不同向共线，
即，
又、夹角为，所以，
所以，解得，
又向量与不同向共线，
所以，解得，
所以的取值范围是且.
57．已知向量，．
(1)若，求实数k的值；
(2)若与的夹角是钝角，求实数k的取值范围．
【答案】(1)k＝
(2)．
【分析】（1）先求出，然后再根据垂直关系即可求出；
（2）由与的夹角是钝角得到且与方向不相反，得到不等式组，求出实数k的取值范围.
【详解】（1），
因为，所以，
解得：.
（2）若与的夹角是钝角，
则且与方向不相反，
即，且
解得：且，
故实数k的取值范围是.
58．若两个非零向量满足，则向量与的夹角为（ ）
A．B．C．D．
【答案】B
【分析】根据向量夹角公式结合数量积公式计算求解.
【详解】设向量与的夹角为θ.
由，左右两边平方得,得.
由，得，从而.
故选:B.
59．已知单位向量与互相垂直，且，记与的夹角为，则（ ）
A．B．C．D．
【答案】D
【分析】根据数量积的运算律可得出，.然后根据数量积的定义，即可得出答案.
【详解】由已知可得，，
，所以，.
根据数量积的定义可知，.
故选：D.
考点11求投影向量
60．已知的外接圆的圆心为，且，，则向量在向量上的投影向量为（ ）
A．B．C．D．
【答案】B
【分析】先判断出为直角三角形，再结合求出，最后根据投影向量的计算方法计算即可得正确的选项.
【详解】
因为，故为的中点，而为外心，
故为直角三角形，且，
取的中点为，连接，则，
因为，故，故，
而为锐角，故，故，所以，
而向量在向量上的投影向量为，
故选：B.
61．已知向量，，则在上的投影向量的模为______．
【答案】
【分析】根据数量积以及模的坐标表示，求出数量积以及模，然后根据投影向量的概念，即可得出答案.
【详解】由已知可得，，，
所以，在上的投影向量的模为.
故答案为：.
62．已知向量，且满足，则向量在向量上的投影向量为（ ）
A．B．C．D．
【答案】C
【分析】根据求出，再根据投影向量公式可求出结果.
【详解】因为，所以，得，
所以，，
所以向量在向量上的投影向量为.
故选：C
63．已知，，与的夹角为，则在方向上的投影向量为（ ）
A．B．C．D．
【答案】C
【分析】直接利用在方向上投影向量公式计算即可得出结果.
【详解】在方向上的投影向量为，
故选：C
64．（多选）若过作的垂线，垂足为，则称向量在上的投影向量为．如图，已知四边形均为正方形，则下列结论正确的是（ ）

A．在上的投影向量为
B．在上的投影向量为
C．在上的投影向量为
D．在上的投影向量为
【答案】AC
【分析】过作于，连接，设，由可得，求出可得，可得在上的投影向量； 根据向量加法的平行四边形法则得，可得在上的投影向量．
【详解】过作于，连接，
因为，，所以四边形为平行四边形，
设，则，，
由可得，
所以，则，所以在上的投影向
量为，
根据向量加法的平行四边形法则，得，
所以在上的投影向量为．
故选： AC.

65．已知，若与的夹角为，则在上的投影向量为______.
【答案】
【分析】先利用数量积定义及运算律求出和，再利用投影向量的定义求解即可.
【详解】因为，与的夹角，则，
所以，
所以在上的投影向量为.
故答案为：
考点12最值、范围问题
66．已知是单位向量，向量满足，则的取值范围是（ ）
A．B．
C．D．
【答案】C
【分析】利用向量数量积公式得到，结合，得到不等式，求出的取值范围.
【详解】设的夹角为，由题意得，
因为是单位向量，故，显然，且，
所以，
因为，所以，
所以，解得.
故选：C
67．已知正方形ABCD的边长为2，P为正方形ABCD内部（不含边界）的动点，且满足，则的取值范围是______.
【答案】
【分析】根据题意建立合适的平面直角坐标系并求出相应点的坐标，设点，代入中，再由角的取值范围即可求得的取值范围.
【详解】已知正方形的边长为2，建立如图所示的平面直角坐标系，
则，
又为正方形内部不含边界的动点，且满足，所以P在以AB为直径的半圆上（不包含端点），
，则，
又，则.
故答案为：.
68．（多选）如图放置的边长为1的正方形的顶点分别在轴、轴正半轴上（含原点）上滑动，则的值可能是（ ）
A．1B．
C．2D．
【答案】AC
【分析】令，由边长为1的正方形的顶点、分别在轴、轴正半轴上，可得出，的坐标，由此可以表示出两个向量，由坐标运算即可求解．
【详解】如图令，由于故，，
如图，，故，，
故，
同理可求得，即，
，，
，
故选：AC
69．在中，，为边上的动点，则的最小值为_________．
【答案】/-2.56
【分析】根据题意，建立直角坐标系，运用坐标表示向量，用数量积求解即可．
【详解】由于，所以为原点，为轴，为轴，建立直角坐标系如图所示：

则有：，
设点，且，
所以，
则，
当时，取得最小值．
故答案为：．
70．如图，已知是以为直径的上半圆上的动点（包含端点，），是的中点，，则的最大值是______．

【答案】2
【分析】设，则，据此可得答案.
【详解】因为，所以，所以，当且仅当，即与重合时取等号，故的最大值是2．
故答案为：2
71．在中，若，，则面积的最大值为______．
【答案】2
【分析】作出辅助线，利用向量线性运算得到，利用三角形面积公式求出最值.
【详解】设点为线段的三等分点，
因为，，
所以，，
则，
当且仅当时，等号成立，
故面积的最大值为2.

故答案为：2